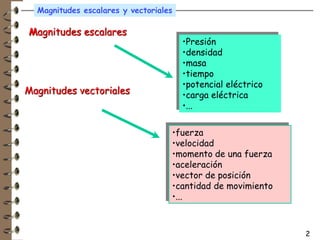
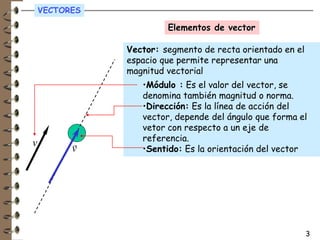
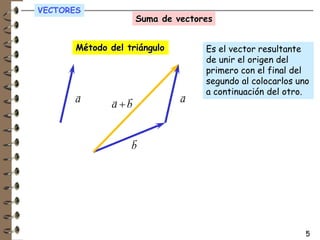
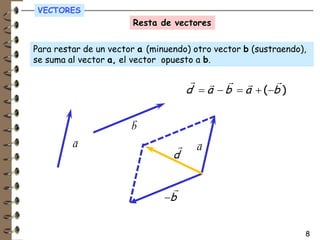
Las magnitudes físicas pueden ser escalares o vectoriales. Las magnitudes escalares solo requieren un valor numérico para definirse, mientras que las magnitudes vectoriales también necesitan una dirección y sentido. Algunas magnitudes escalares son la temperatura y el tiempo, mientras que magnitudes vectoriales incluyen la velocidad y la fuerza.

1. Magnitudes escalares y vectoriales
Magnitud escalar:
Magnitud física que queda totalmente definida mediante un valor
numérico y su unidad.
Magnitud vectorial:
Magnitud física que necesita para quedar definida, además de un
valor numérico y su unidad, una dirección y un sentido.
Magnitudes escalares:
Magnitudes vectoriales:
Temperatura (23 ºC) r
r r
Masa (10 g) Velocidad (2i + 3 j + 1k )m / s
r
Tiempo (5 s) Fuerza (2k ) N
Longitud (15 mm)
1

2. Magnitudes escalares y vectoriales
Magnitudes escalares
•Presión
•densidad
•masa
•tiempo
•potencial eléctrico
Magnitudes vectoriales •carga eléctrica
•...
•fuerza
•velocidad
•momento de una fuerza
•aceleración
•vector de posición
•cantidad de movimiento
•...
2

3. VECTORES
Elementos de vector
Vector: segmento de recta orientado en el
espacio que permite representar una
magnitud vectorial
Vector:
•Módulo : Es el valor del vector, se
denomina también magnitud o norma.
•Dirección: Es la línea de acción del
vector, depende del ángulo que forma el
vetor con respecto a un eje de
referencia.
v r
v •Sentido: Es la orientación del vector
3

4. VECTORES
Propiedades de los vectores
r
a.v
Producto de un vector por un escalar a (a>0)
Misma dirección y sentido
Módulo multiplicado por a
r
av
r
v
r Vector unitario
v
Misma dirección y sentido
r Módulo unitario (1)
uv
r
r v
uv 
v
4

5. VECTORES
Suma de vectores
Método del triángulo Es el vector resultante
de unir el origen del
primero con el final del
segundo al colocarlos uno
r r a continuación del otro.
a r r a
a +b
r
b
5

6. VECTORES
Suma de vectores
Método del paralelogramo
suma de dos vectores:
r la diagonal del
a r r
a +b paralelogramo obtenido
al poner ambos vectores
r con el origen común.
a
r
b
6

7. VECTORES
Suma de vectores
Método del polígono
c
r
b
c
r r
a b
r
a
a +b +c
Se ponen uno a continuación del otro, con la misma orientación. La suma
es un vector con origen en el primero y fin en el último.
7

8. VECTORES
Resta de vectores
Para restar de un vector a (minuendo) otro vector b (sustraendo),
se suma al vector a, el vector opuesto a b.
d  a  b  a + (b )
r
b
r r
a a
d
b
8

9. VECTORES
PRODUCTO ESCALAR
Es el producto de los
módulos por el coseno
del ángulo que forman
los dos vectores a
r
a
r
b
rr r r
a·b  a ·b cos a
9

10. VECTORES
Producto vectorial
producto vectorial:
Es un vector de r r
a b
módulo el producto
de los módulos por el
seno del ángulo que r
forman los dos b
vectores, dirección r
normal al plano que a b
forman, y sentido el r
que hace a los tres a
vectores un triedro r
a
a derechas, yendo
del primero hacia el
segundo por el
camino más corto.
Regla de la mano a  b  a · b sena
derecha o del avance
de un tornillo
10

11. VECTORES
Resumen
suma
r r
r
r a +b
a
a·v
producto por
r
b
un escalar
r r
v b
r r
a b
producto escalar r
a
producto vectorial
a
r
a
r a  b  a · b sen a
b
rr r r
a·b  a ·b cos a
11

12. VECTORES
Componentes de un vector
Las componentes de un
Z
vector en un sistema
de referencia son las
coordenadas del punto
final del vector al
colocar el origen del
vz r vector en el origen del
v sistema de referencia
(vx,vy,vz)
(vx, vy, vz).
vz
O Y
vx vy
vx
vy
X El módulo de un vector se r
puede calcular a partir de v  v x + v 2 + vz
2
y
2
sus componentes como:
12

13. VECTORES
Cosenos directores
Z
Son los cosenos de
los ángulos a, b y g
que forma el vector
vz r con los ejes del
g v
(vx,vy,vz) sistema de
referencia.
O b
Y
vx a vy
r
v x  v cos a
r
v y  v cos b
X r
vz  v cos g
13

14. VECTORES
Vectores unitarios
Z
Los unitarios en el
sentido positivo de los
ejes de un sistema de
referencia, i, j, k, son
los vectores que
r forman la base
k r ortogonal del sistema
j de referencia.
O Y
r r
i i i
r
j j
X r
k k
14

15. VECTORES
Vectores unitarios
Z
producto escalar
rr rr rr
 i ·i  1 i · j  0 i ·k  0
rr r r r r rr rr
a ·b  a ·b cos a  j ·i  0 j · j  1 j ·k  0
rr r rr
k ·i  0 k ·r  0 k ·k  1
 j
r
k r
j
O Y
r
i producto vectorial
r r r r r r r r
 i i  0 i  j  k i k   j
r r r r r r r r r r r r
X a  b  a ·b sin a  j  i  k j j 0 j k  i
r r r r r r
 k  i  r k  r  i k  k  0
 j j
15

16. VECTORES
Operaciones por componentes
suma
r
r r r r
a + b  a x i + a y j + az k  + bx i + by j + bz k  
r r
a +b
a r r r r
r
 a x + bx i + a y + by  j + az + bz k
r r
r
b
producto escalar
rr r r
a·b  a x i + a y j + az k bx i + by j + bz k  
a r r r r
r ·
a
 a x ·bx  + a y ·by  + az ·bz 
r
b
producto vectorial
a
b   
a  b  ax i + a y j + az k  bx i + by j + bz k  
a
i j k
 ax ay az
r r bx by bz
a b 16

17. VECTORES
Determinantes
a11 a12 a13
b21 b22 b23   a11b22c33 + a12b23c31 + a13b21c32  
c31 c32 c33   a13b22c31 + a11b23c32 + a12b21c33 
producto vectorial
r r
  
r r r r r r
a  b  a x i + a y j + a z k  bx i + by j + bz k 
r r r
r
i j k
a
b
 ax ay az 
r
a bx by bz
  ay bz  az by   i +  azbx  axbz   j +  axby  a ybx   k
r r
a b FUENTE: INTERNET 17