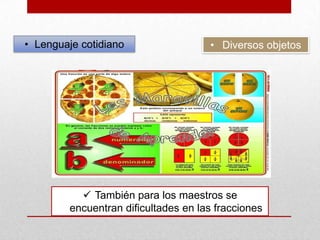
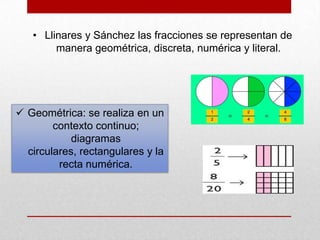
El documento discute las fracciones, incluyendo sus definiciones, dificultades de enseñanza y aprendizaje, y sugerencias didácticas. Las fracciones se definen como números que se obtienen de dividir una totalidad en partes iguales. Los principios que deben regir su enseñanza incluyen que los estudiantes construyan el conocimiento por sí mismos y se valoren sus propios métodos de resolución de problemas. Las fracciones pueden representarse de forma geométrica, numérica y literal.

1.  PROCESOS COGNITIVOS Y CAMBIO
CONCEPTUAL EN MATEMÁTICAS Y CIENCIA
NORMALISTA: HUGO ENRIQUE GARZA AHUMADA

2. FRACCIONES
 Es número que se obtiene de dividir
una totalidad en partes iguales.
 La matemática se entiende como un medio para
aprender y resolver problemas.
estrategias
actitudes
soluciones

3. Cuando se trata de explicar a los alumnos, estos
presentan algunas dificultades que van desde:
• No existe una noción de reparto.
• No comprende la función del
numerador y denominador.

4. • Lenguaje cotidiano
• Diversos objetos
 También para los maestros se
encuentran dificultades en las fracciones

5. A manera de sugerencia didáctica, los principios que deben
regir la enseñanza de las fracciones, según L. Streefland, son:
• Lo importante es que los propios niños "construyan" las
operaciones con fracciones. Construcción que debe basarse
en
las
propias
actividades
del
alumno,
como:
estimación, desarrollo del sentido del orden y tamaño...
• Valorar las actividades de los alumnos, así como los métodos
y procedimientos que utilicen para resolver problemas, aunque
difieran de la formalidad propia de la materia.

6. • Que el alumno sea capaz de formular sus propias reglas y
generalizaciones para adquirir su conocimiento.
• Se deben utilizar los saberes previos del alumno como base
para empezar la secuencia de la enseñanza de fracciones
(ideas relativas a mitades, tercios, cuartos, etc., los procesos
básicos de dividir, repartir,...)
Esta postura defiende la idea de que son los alumnos los que
tienen que construir el conocimiento de fracción, no el
profesor.

7. Cuando un maestro es principiante en algún momento
se encontrará con fracciones para enseñar
 Explicación clara.
 Le da valor.
 La enseñanza es eficiente

8. • Si no se logra una buena explicación, las
fracciones se vuelven frustrante para los
alumnos.
 Según Sally: Las fracciones pueden ser las
causantes de su matefobia.

9. Entonces los maestros tienen que buscar
elementos que les permitan facilitar y ejercitar las
fracciones.
 El profesor debe estar consciente de que los
conceptos matemáticos son entes abstractos

10.  Los números racionales se expresan de
dos formas.
• Fracciones
• Notación decimal
 La fracciones tienen su origen en las relaciones entre la
aritmética decimal. El uso particular de fracciones
decimales y su utilización para la medida de
magnitudes, como el tiempo da lugar a la notación
decimal.

11. • Llinares y Sánchez las fracciones se representan de
manera geométrica, discreta, numérica y literal.
 Geométrica: se realiza en un
contexto continuo;
diagramas
circulares, rectangulares y la
recta numérica.

12. Las representaciones numéricas se encuentran
en distintas formas de utilizar los números para
indicar una relación parte-todo.
• Representación como división:
3/5
• Representación como razón:
3:5
• Representación decimal:
0.6

13. Representaciones literales: Tres quintos, tres
de cinco y proporción de tres a cinco.
Según Moisés Coriat, las fracciones se expresan de
forma sintética; con cifras, con palabras y mediante
magnitudes.