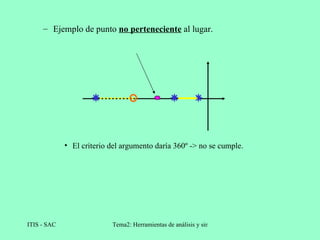
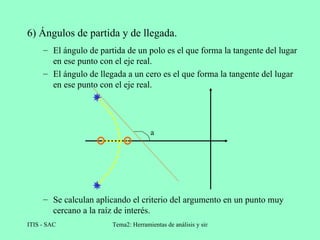
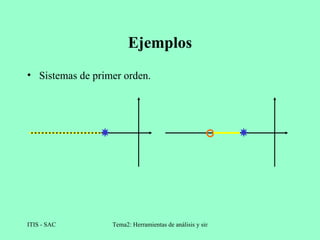
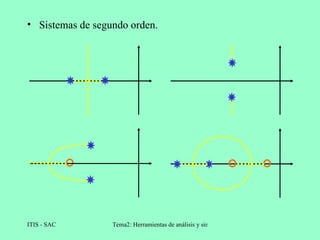
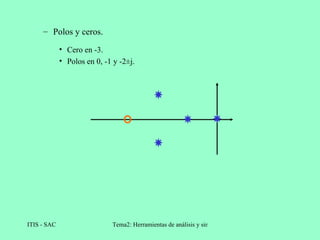
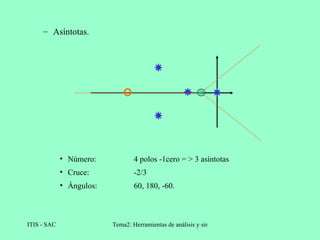
El lugar de las raíces es una técnica gráfica que representa la posición de los polos de un sistema de realimentación cuando varía un parámetro como la ganancia. Se construye trazando las raíces de la ecuación característica para diferentes valores del parámetro. Esto permite analizar la estabilidad y respuesta del sistema cuando cambia ese parámetro.

1. El lugar de las raíces

2. Introducción Los sistemas realimentados son un tipo especial de sistemas muy empleados en control. La tarea de diseño consiste en ajustar los parámetros variables de la parte de control para conseguir el comportamiento global deseado. El lugar de las raíces es una técnica gráfica empleada en el análisis y diseño de sistemas de control . Sistema Control + -

3. Definición Dado un sistema realimentado del tipo La técnica del lugar de las raíces permite conocer cómo varían los polos del sistema en bucle cerrado cuando se modifica el valor del parámetro de interés . G(s) K + - R(s) Y(s)

4. Expresión de la función de transferencia Los polos en bucle cerrado vienen dados por las raíces de la ecuación característica. G(s) K + - R(s) Y(s) El lugar de las raíces representa gráficamente sobre el plano s , las posiciones de los polos de M(s) cuando K varía entre 0 e infinito.

5. Ejemplo de lugar de las raíces.

6. Criterio del módulo y criterio del argumento A partir de la ecuación característica tenemos Para que un punto s i pertenezca al lugar de las raíces deben darse dos condiciones: A) Criterio del módulo : B) Criterio del argumento : donde p es un número entero.

7. Evaluación gráfica del criterio del módulo y del argumento. s i -p 1 -p 2 -p 3 -c 1 m p3 a c1 Los ángulos se toman con respecto al semieje real positivo, y en sentido antihorario.

8. Reglas de construcción 1) Expresar la ecuación característica en la forma Donde K es el parámetro de interés y G es una función en s . Generalmente, el parámetro de interés suele ser la ganancia del sistema en bucle abierto, aunque el método es válido para cualquier otro parámetro.

9. 2) Situar los polos y ceros del sistema en bucle abierto. Descomponiendo la función de transferencia en bucle abierto en numerador y denominador, la ecuación característica queda Deberán situarse entonces los polos ( D(s)=0 ) y los ceros ( N(s)=0 ) del sistema sobre el plano s. Suele emplearse el símbolo “*” para los polos y el “o” para los ceros.

10. Para la ecuación característica D(s)+KN(s)=0 , en los extremos de variación del parámetro tenemos Luego el lugar de las raíces parte ( K=0 ) de los polos del sistema en bucle abierto y llega ( K=  ) a los ceros .

11. Ejemplo: (s+2)/(s+1) K + - R(s) Y(s) Ecuación característica: K=0: K=1: K=10: K=100: K=1/2:

12. s=-1 s=-2 (K=0) (K=  )

13. 3) Número de ramas y simetría. El lugar de las raíces tiene un número de ramas igual al orden del sistema (número de polos). Para un sistema con n polos y m ceros, existirán n-m ramas asintóticas (tienden a un cero en el infinito). El lugar es simétrico con respecto al eje real del plano s.

14. La región donde se encuentran dos ramas del lugar da origen a puntos de ruptura (confluencia/dispersión).

15. 4) Lugar sobre el eje real. Existe lugar sobre el eje real en aquellas secciones que dejan un número impar de polos+ceros a su derecha.

16. Ejemplo de punto no perteneciente al lugar. El criterio del argumento daría 360º -> no se cumple.

17. 5) Centroide y asíntotas. Las asíntotas intersectan sobre el eje real en un punto que viene dado por la siguiente expresión: donde n es el número de polos y m el número de ceros de G(s). 

18. El ángulo que forman las asíntotas con el eje real se calcula como sigue  1

19. 6) Ángulos de partida y de llegada. El ángulo de partida de un polo es el que forma la tangente del lugar en ese punto con el eje real. El ángulo de llegada a un cero es el que forma la tangente del lugar en ese punto con el eje real. a Se calculan aplicando el criterio del argumento en un punto muy cercano a la raíz de interés.

20. 7) Intersección con el eje imaginario. Criterio de Routh-Hurwitz (límite de la estabilidad). Se obtiene el valor límite del parámetro y se resuelve la ecuación característica para ese valor.

21. 8) Puntos de ruptura (confluencia/dispersión). Donde el lugar de las raíces abandona el eje real. Se obtienen a partir de la expresión.

22. Ejemplos Sistemas de primer orden.

23. Sistemas de segundo orden.

24. Ejercicio Trazar el lugar de las raíces frente a la ganancia en bucle abierto K para el siguiente sistema. G(s) K + - R(s) Y(s) Donde.

25. Ecuación característica. Función de transferencia. Ecuación característica.

26. Polos y ceros. Cero en -3. Polos en 0, -1 y -2±j.

27. Lugar sobre el eje real.

28. Asíntotas. Número: Cruce: Ángulos: 4 polos -1cero = > 3 asíntotas -2/3 60, 180, -60.

29. LdR.

30. Aplicaciones El lugar de las raíces puede emplearse para diferentes propósitos: Ajuste/sintonización de parámetros internos. Obtención de valores adecuados para los parámetros variables de un sistema con el fin de obtener una mejor respuesta. Diseño de controladores. Diseño de unidades externas al sistema para controlar su funcionamiento. Estudio de estabilidad. Análisis de la estabilidad absoluta y relativa de un sistema frente a un parámetro determinado. Robustez. Sensibilidad de un sistema ante variaciones de un parámetro de interés.