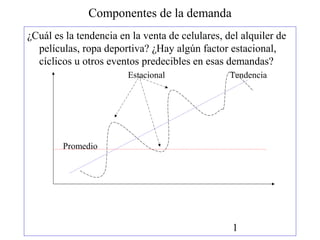
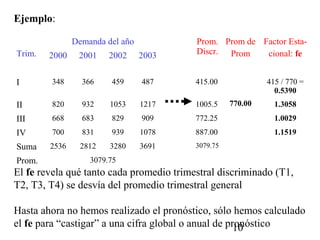
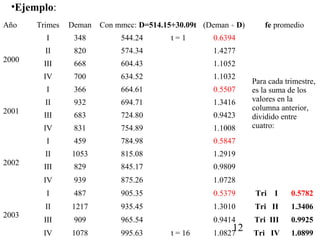
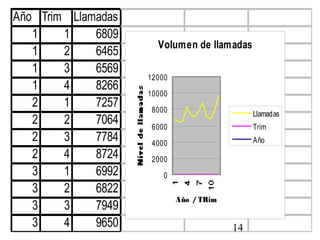
Este documento describe diferentes métodos para realizar pronósticos, incluyendo promedios móviles simples y ponderados, suavizamiento exponencial, regresión lineal simple y series de tiempo. Explica conceptos como estacionalidad, ciclicidad y autocorrelación. También incluye ejemplos numéricos para ilustrar cómo aplicar cada método de pronóstico.

1. Componentes de la demanda
¿Cuál es la tendencia en la venta de celulares, del alquiler de
películas, ropa deportiva? ¿Hay algún factor estacional,
cíclicos u otros eventos predecibles en esas demandas?
Estacional Tendencia
Promedio
1

2. ANÁLISIS DE MÉTODOS CUANTITATIVOS
A. Promedio Móvil Simple
Sem 1 2 3 4 5 6 7 8 9 10 11 12
Dem 650 678 720 785 859 920 850 758 892 920 789 844
Asuma que sólo tiene 3 semanas y 6 semanas de datos de
demanda actual para el pronóstico
1 2 3 4 5 6 7 8 9 10 11 12
3 683 728 788 854
Sem
6 769 802 815
Sem
Grafique la demanda real con los respectivos pronósticos y
comente. Si el periodo seleccionado es 4, ¿cambia su opinión?
2

3. B. Promedio Móvil Ponderado
Sem Demanda Peso Pron Periodo
01 650 0.2 t-3
02 678 0.3 t-2
03 720 0.5 t-1
04 693
El periodo “t” refiere el periodo para el cual se
calcula el pronóstico
693 = 720x0.5 + 678x0.3 +650x0.2
3

4. C. Suavizamiento Exponencial
Ft = Ft-1 + α (At-1 – Ft-1), donde:
Ft : Pronóstico para el periodo t α : Factor de ponderación
Ft-1 : Último pronóstico At-1 : Última demanda real
- La más reciente demanda puede tener la más alta ponderación
- La importancia de los datos disminuye en la medida en que el
pasado se hace más distante
- Cada incremento del pasado disminuye en (1- α)
- α determina el nivel de uniformidad y la velocidad de reacción a
las diferencias entre las proyecciones y las demandas reales. Se
determina por la naturaleza del producto; si la demanda es
estable asume un valor relativamente pequeño
Por ejemplo, ponderaciones con α = 0.050
Ponderación más reciente = α(1 – α)0 0.0500
Datos anteriores en un periodo de tiempo = α(1 – α)1 0.0475
Datos anteriores en dos periodo de tiempo = α(1 – α)2 0.0451
Datos anteriores en tres periodo de tiempo = α(1 – α)3 0.0429
Datos anteriores en n periodo de tiempo = α(1 – α)n 4 ---

5. •Ejemplo. Determine el pronóstico con Suavizamiento exponencial para
los periodos del 2 al 10, usando α = 0.1 y α = 0.6
Sem 1 2 3 4 5 6 7 8 9 10
Dem 820 775 680 655 750 802 798 689 775
0.1 820 820 815.5 802 787.3 783.5 785.4 786.6 776.9 776.7
0.6 820 820 793 723.2 683.1 723.2 770.5 787 728.2 756.3
usando α = 0.1
F2 = 820 + 0.1(820 – 820) = 820 F3 = 820 + 0.1(775 – 820) = 815.5
F4 = 815.5 + 0.1(680 – 815.5) = 802 F5 = 802 + 0.1(655 – 802) = 787.3
... F10 = 776.9 + 0.1(775 – 776.9) = 776.7
Supuesto: La demanda de la semana 01 (A1) se asume igual al pronóstico
01 (F1). Verifique los valores para 0.6
5

6. Ejemplo: El pronóstico para el periodo 10 usando α = 0.6 y las
cuatro demandas más recientes
F10 = 0.6(1-0.6)0(775) + 0.6(1-0.6)1(689) + 0.6(1-0.6)2(798) +
0.6(1-0.6)3(802) + (1-0.6)4(766) = 1067.37
766 = Ft-4 = (775+689+798+802) ÷ 4 = pronóstico aproximado del
periodo “t-n”, aplicado si no se da el valor calculado previamente
La expresión resaltada en verde es de la forma:
Ft = α(1- α)0(At-1) + α(1- α)1(At-2) + α(1- α)2(At-3) + α(1- α)3(At-4)
+ (1- α)4(Ft-4), que es una extensión de la fórmula dada al
inicio de este apartado
¡La deducción puede revisar en Administración de la Producción y
las Operaciones – Everett – página 102! 6

7. D) Modelo de Regresión Lineal Simple
Yt = a + bx
- b es la pendiente de la recta calculado a partir de todos los datos
- Base para procesar la información de pronósticos causales y el
análisis de series de tiempo
- Pronósticos causales: Una variable explica el comportamiento de la
demanda
- Serie de tiempo. El tiempo explica el comportamiento de la
demanda. No existe evidencia clara de otro factor
- Calculando a y b:
a = y – bx b = (Σxy – n(y)(x)) / (Σx2 – n(x)2)
7

8. Ejemplo:
Semana Venta Semana (x) X2 Venta (y) (XY)
01 150 1 1 150 150
02 157 2 4 157 314
03 162 3 9 162 486
04 166 4 16 166 664
05 177 5 25 177 885
3 55 162.4 2499
Promedio Suma Promedio Suma
Aplicando la fórmula, Y = 143.5 + 6.3(t=x)
¿Qué observaciones haría a este modelo?
8

9. E) Pronósticos con base en series de tiempo
- Serie de tiempo: datos ordenados cronológicamente, los mismos
que pueden contener uno o más componentes de la demanda
- Estacionalidad: comparando el mismo periodo año tras año.
Periodo de año con marcado nivel de actividad
- Ciclicidad: relativo a ciclos, los mismos que pueden durar meses o
años y son de más difícil identificación. Cíclico se utiliza para
indicar los periodos diferentes de aquellos recurrentes en el año
- Autocorrelación: una variable explica a la otra
- Aleatoriedad: cualquier causa que afecta la demanda, que no tiene
una frecuencia o explicación coherente
- Variación estacional aditiva: Pronóstico = Tendencia + f.e.
- Variación estacional multiplicativa: Pron = Tendencia x f.e.
- Factor estacional: cantidad de corrección necesaria en las series de
tiempo para ajustar a una estación del año
9

10. Ejemplo:
Demanda del año Prom. Prom de Factor Esta-
Trim. 2000 2001 2002 2003 Discr. Prom cional: fe
I 348 366 459 487 415.00 415 / 770 =
0.5390
II 820 932 1053 1217 1005.5 770.00 1.3058
III 668 683 829 909 772.25 1.0029
IV 700 831 939 1078 887.00 1.1519
Suma 2536 2812 3280 3691 3079.75
Prom. 3079.75
El fe revela qué tanto cada promedio trimestral discriminado (T1,
T2, T3, T4) se desvía del promedio trimestral general
Hasta ahora no hemos realizado el pronóstico, sólo hemos calculado
el fe para “castigar” a una cifra global o anual de pronóstico
10

11. Ejemplo: Si de acuerdo a la tasa de crecimiento promedio anual, la
demanda pronosticada para el 2004 ha sido 4076 (3691+385),
entonces esta cantidad se distribuye a lo largo del año según el
siguiente procedimiento:
Tri I: (Pronóstico ÷ 4)(fe) = (4076 ÷ 4)(0.5390) = 549.241
Tri II: 1330.6102
Tri III: 1021.9551
Tri IV: 1173.7861
Los fe pueden actualizarse con la demanda real del año 2004, ya sea
con 5 ó 4 años de demanda agrupada por trimestres como siempre.
Estos fe servirán para pronosticar la demanda del año 2005, p.e.
Ejercicio: Describir el procedimiento que corresponda cuando los
datos de demanda anual están estacionalizados (agrupados):
a) Cada dos meses
b) Cada cuatro meses
Puede utilizarse también el procedimiento de MMCC para calcular a
la vez los fe y los pronósticos trimestrales...Veamos el ejemplo:
11

12. •Ejemplo:
Año Trimes Deman Con mmcc: D=514.15+30.09t (Deman ÷ D) fe promedio
I 348 544.24 t=1 0.6394
II 820 574.34 1.4277
2000
III 668 604.43 1.1052
IV 700 634.52 1.1032
Para cada trimestre,
I 366 664.61 0.5507 es la suma de los
II 932 694.71 1.3416 valores en la
2001 columna anterior,
III 683 724.80 0.9423 dividido entre
IV 831 754.89 1.1008 cuatro:
I 459 784.98 0.5847
II 1053 815.08 1.2919
2002
III 829 845.17 0.9809
IV 939 875.26 1.0728
I 487 905.35 0.5379 Tri I 0.5782
II 1217 935.45 1.3010 Tri II 1.3406
2003
III 909 965.54 0.9414 Tri III 0.9925
IV 1078 995.63 t = 16
12
1.0827 Tri IV 1.0899

13. ... Continúa el ejemplo anterior
- Los pronósticos trimestrales para el año 2004 son las
proyecciones calculadas con la ecuación D = 514.15 + 30.09t,
desde t = 17 hasta t = 20, multiplicados por el fe que corresponda
en cada trimestre
- Tri I = (514.15 + 30.09x17)(0.5782) = 593.05
- Tri II = (514.15 + 30.09x18)(1.3406) = 1415.36
- Tri III = (514.15 + 30.09x19)(0.9925) = 1077.72
- Tri IV = (514.15 + 30.09x20)(1.0899) = 1216.27
Al cociente (Demanda real) ÷ fe se le conoce como demanda
descestacionalizada y la serie de datos generada indica lo que
“habrían” sido las ventas, manteniendo la tendencia, al margen de los
factores estacionales. Utilizando los fe calculados con mmcc se tiene:
Dd1 = 348 ÷ 0.5782 = 601.86 Dd2 = 820 ÷ 1.3406 = 611.67
Dd3 = 668 ÷ 0.9925 = 673.05 Dd4 = 700 ÷ 1.0899 = 642.26
... Dd16 = 1078 ÷ 1.0899 = 989.08
¡Verifique la tendencia de los valores Ddi!
13

14. Año Trim Llamadas
1 1 6809
Volumen de llamadas
1 2 6465
1 3 6569
12000
1 4 8266
10000
2 1 7257 8000
Llamadas
2 2 7064 .
6000 Trim
2 3 7784 4000 Año
2 4 8724 2000
3 1 6992 0
3 2 6822
Año / TRim
3 3 7949
3 4 9650 14