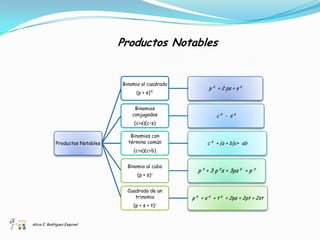
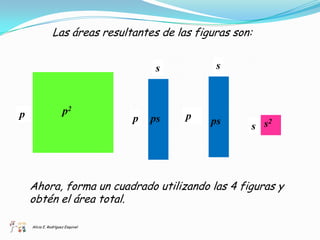
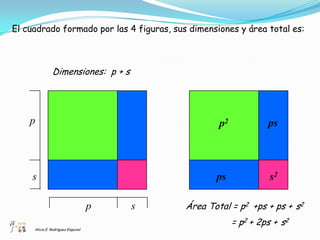
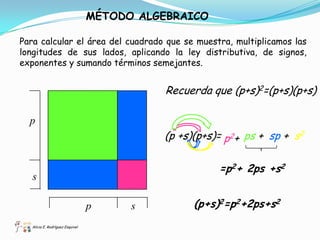
El documento presenta un enfoque didáctico para enseñar el concepto del binomio al cuadrado utilizando métodos geométricos y algebraicos. Se explican las fórmulas y aplicaciones de diferentes productos notables, así como la vinculación entre el álgebra y la geometría. Además, se proponen ejercicios prácticos para reforzar el aprendizaje.

1. Diseño y Selección de Recursos Didácticos
en el Desarrollo de las Competencias
“Binomio al cuadrado”
Facilitadora: Marta Patricia Ruiz López
Alumna: Alicia Rodríguez Esquivel
Marzo de 2012

2. Propósitos. El alumno conoce los diferentes
productos notables y deduce la regla general de un
binomio al cuadrado, aplicando dos métodos:
Geométrico.- Vinculando la geometría con el
álgebra, aplicando las fórmulas de áreas de
cuadrados y rectángulos.
Algebraico.- Aplicando leyes de signos, exponentes,
ley conmutativa, asociativa y distributiva en
expresiones algebraicas.
Alicia E. Rodríguez Esquivel

3. Productos Notables
Binomio al cuadrado
p² + 2 ps + s²
(p + s)²
Binomios
conjugados c² - s²
(c+s)(c-s)
Binomios con
Productos Notables término común c² + (a + b)c+ ab
(c+a)(c+b)
Binomio al cubo
p³ + 3 p²s + 3ps² + p³
(p + s)³
Cuadrado de un
trinomio p² + s² + t² + 2ps + 2pt + 2st
(p + s + t)³
Alicia E. Rodríguez Esquivel

4. GEOMETRICAMENTE
Recuerda que el área de un:
 rectángulo es Ar =b*a
cuadrado está dado por: Ac = l* l = l²
 Obtén las áreas de las figuras que se te
solicitaron:
o 1 cuadrado verde, cuyo longitud del lado es “p” unidades
o1 cuadrado rosa, la dimensión de su lado es “s” unidades
o2 rectángulos azules, las dimensiones son de base “s”
unidades u de altura “p” unidades.
Alicia E. Rodríguez Esquivel

5. Las áreas resultantes de las figuras son:
s s
p p2 p
p ps ps 2
s s
Ahora, forma un cuadrado utilizando las 4 figuras y
obtén el área total.
Alicia E. Rodríguez Esquivel

6. El cuadrado formado por las 4 figuras, sus dimensiones y área total es:
Dimensiones: p + s
p p2 ps
a
s ps s2
p s Área Total = p2 +ps + ps + s2
= p2 + 2ps + s2
Alicia E. Rodríguez Esquivel

7. MÉTODO ALGEBRAICO
Para calcular el área del cuadrado que se muestra, multiplicamos las
longitudes de sus lados, aplicando la ley distributiva, de signos,
exponentes y sumando términos semejantes.
Recuerda que (p+s)2=(p+s)(p+s)
p
(p +s)(p+s)= p2+ ps + sp + s2
=p2+ 2ps +s2
s
p s (p+s)2=p2+2ps+s2
Alicia E. Rodríguez Esquivel

8. Observa, ¡¡ con los dos métodos llegamos al mismo
resultado!!.
(p + s)² = p² + 2ps + s²
Ahora escribe en lenguaje algebraico la regla que acabas
de deducir, considerando que:
p = primer término
s = segundo término
1. El cuadrado del primer término (p)² +
2. El doble producto del primer término por el
segundo (2ps) (respetando leyes de signos) +
3. El cuadrado del segundo término (s)²
Alicia E. Rodríguez Esquivel

9. Ahora, refuerza tu aprendizaje a través de los siguientes
applets:
Binomio al cuadrado Ejemplos numéricos
Práctica y relaciona los productos con áreas de figuras
geométricas. Vincula el algebra y la geometría
Video geométrico
Video algebraico
Alicia E. Rodríguez Esquivel

10. Ahora, ¡ a practicar !:
A) 9x2 + 12x - 16
a) (3x – 4)2 = B) 9x2 – 24x + 16
C) 9x2 - 16
D) 9x2 - 12x + 16
Elige la respuesta correcta:
A B C D
Alicia E. Rodríguez Esquivel

11. Alicia E. Rodríguez Esquivel

12. Alicia E. Rodríguez Esquivel

13. Fuentes:
1.- Baldor, Aurelio. (2004). Álgebra. Publicaciones Cultural, S.A. de C.V. México
2.- O'Daffer, Phares G., et al., (1998). Introducción al álgebra, Prentice Hall; México.
3.- Larson/Hostetler, (1999). Álgebra. Publicaciones Cultural, S.A. de C.V. México.
4.- http://arquimedes.matem.unam.mx/Vinculos/Secundaria/3_tercero/3_Matematicas/INTERACTIVOS/3m_b01_t01_s01_descartes/index.html
Alicia E. Rodríguez Esquivel