Este documento presenta cuatro ejemplos de cálculo de áreas de regiones planas limitadas por funciones. En cada ejemplo se calcula el área exacta de la región particionando el dominio e integrando funciones continuas. Se utilizan técnicas como cambios de variable y aplicación del teorema fundamental del cálculo. En el ejemplo 4 se determina adicionalmente una constante para modelar la desforestación de un sembradío.

1. Matemática II
Sesión 5

2. Elaborado por Elsa Guédez
Matemática II
Cálculo de áreas

3. Elaborado por Elsa Guédez
Considera la región “W” limitada por: y = 4x – x2 ˄ y = 0
a) Calcular el área exacta de “W”.
CÁLCULO DEL ÁREA DE UNA REGIÓN PLANA
Ejemplo 1:

4. Elaborado por Elsa Guédez
Se asumirá constante a F(x) = 4x – x2 en cada subintervalo y
dada por su valor en el punto muestra respectivo:
Solución a) Ejemplo 1

5. Elaborado por Elsa Guédez
Solución b) Ejemplo 1
Se considerará: t∈ [0, 4]

6. Elaborado por Elsa Guédez
Por lo tanto, el área “A” de la región viene dada por:
Solución b) Ejemplo 1
Dada la continuidad de la función a integrar, es posible la
aplicación del Teorema fundamental del Cálculo.
Integrando queda:

7. Elaborado por Elsa Guédez
Sustituyendo (2) en (1) resulta:
Solución b) Ejemplo 1
Conclusión
El área exacta de la región es 10,66 m2.

8. Elaborado por Elsa Guédez
Considera la región “W” limitada por: x = y2 - 9 ˄ y = 3 - x
Calcular el área exacta de “W”, particionando en y ∈ [-4,3].
CÁLCULO DEL ÁREA DE UNA REGIÓN PLANA
Ejemplo 2:

9. Elaborado por Elsa Guédez
Solución Ejemplo 2
Se tiene: , de allí:
Además: , de allí:
Se considerará: t∈ [-4, 3]

10. Elaborado por Elsa Guédez
Solución Ejemplo 2
Se considerará:
La partición de “n” subintervalos para t∈ [-4, 3]
Ancho de cada subintervalo: ∆y.
Puntos muestra: yi
* (Puntos medios de c/subintervalo – optativo)

11. Elaborado por Elsa Guédez
Solución Ejemplo 2
Y el área “A” de la región es:
Dada la continuidad de la función integrando, es posible la
aplicación del Teorema fundamental del Cálculo y calcular el
área “A”.
Conclusión:
2
m
57,16
A 

12. Elaborado por Elsa Guédez
Considera la región “R” limitada por:
Asumiendo “x” e “y” en metros.
CÁLCULO DEL ÁREA DE UNA REGIÓN PLANA
Ejemplo 3
y – x3 = 4
4x = 16 – y2
y = -4
y ≥ -4

13. Elaborado por Elsa Guédez
b) Calcular el área exacta de “W” particionando en x ∈ [-2, 4].
Ejemplo 3
a) Calcular el área exacta de “W” particionando en y ∈ [-4, 4].

14. Elaborado por Elsa Guédez
Solución a) Ejemplo 3
Además: y = -4 con y ≥ -4
Se tiene: y – x3 = 4, de allí:
Asimismo: 4x = 16 – y2, de allí:

15. Elaborado por Elsa Guédez
Solución a) del Ejemplo 3
La gráfica es:

16. Elaborado por Elsa Guédez
Solución a) del Ejemplo 3
El gráfico donde se representa el perímetro de la Zona-1 se
muestra a continuación:
donde:

17. Elaborado por Elsa Guédez
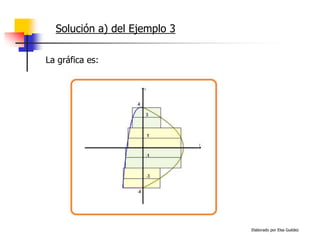
Solución a) del Ejemplo 3
Se considerará: t∈ [-4, 4]
Por lo tanto, el área “A” de la región es:
Dada la continuidad de la función a integrar, es posible la
aplicación del Teorema fundamental del Cálculo, para lo cual se
obtiene de forma inmediata (por el formulario):

18. Elaborado por Elsa Guédez
Hacer el cambio de variable: u = y – 4, y a partir de este
cambio modificar el límite inferior y superior de la integral.
Solución a) Ejemplo 3
Quedando la integral definida:
Para el límite inferior y = -4: se obtiene u = (-4) – 4 = -8,
Para el límite superior y = 4: se obtiene u = (0) – 4 = -4
Se sugiere para la integral que falta resolver:

19. Elaborado por Elsa Guédez
Entonces, el cálculo del área queda:
Solución a) Ejemplo 3
Conclusión
El área exacta de la región es 2
m
33
,
33
3
100
A 


20. Elaborado por Elsa Guédez
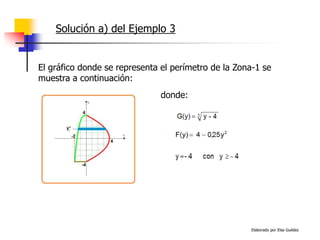
Solución b) del Ejemplo 3
Se tiene y – x3 = 4, de allí: y = x3 + 4  H(x) = x3 + 4
Además, 4x = 16 – y2 , de allí:
Es decir, se tienen dos funciones:
Se considerará:
La partición de “3” subintervalos para x∈ [-2, 4]
Ancho de cada subintervalo: ∆x = 6/3 = 2.
Puntos muestra: Puntos medios de c/subintervalo

21. Elaborado por Elsa Guédez
Solución c) del Ejemplo 3
Se asumirá constante a H(x) , S(x) y U(x), en cada subintervalo
y dada por su valor en el punto muestra respectivo.
Por lo tanto, el área “A” de la región es:
2
3
R
A m
85
,
35


Conclusión:

22. Elaborado por Elsa Guédez
Solución d) del Ejemplo 3
Se asumirá constante a H(x) , S(x) y U(x), en cada subintervalo
y dada por su valor en el punto muestra respectivo.
Se considerarán dos casos:
Caso 1: t∈ [-2, 0]

23. Elaborado por Elsa Guédez
Solución b) del Ejemplo 3
Por lo tanto, el área “A1” de la subregión correspondiente a
x∈ [-2, 0] viene dada por:
Dada la continuidad de la función integrando, es posible la
aplicación del Teorema fundamental del Cálculo y calcular el
área “A1”.
De allí se obtiene A1 = 12
12

24. Elaborado por Elsa Guédez
Solución b) del Ejemplo 3
Caso 2: t∈ [0, 4]
Por lo tanto, el área “A2” de la subregión correspondiente a
x∈ [0, 4] viene dada por:
Dada la continuidad de la función integrando, es posible la
aplicación del Teorema fundamental del Cálculo y calcular el
área “A2”.

25. Elaborado por Elsa Guédez
Haciendo el cambio de variable z = 16 - 4x, para la
integral indefinida:
Se obtiene:
Solución d) del Ejemplo 3
Por lo tanto:

26. Elaborado por Elsa Guédez
Conclusión:
El área de la región es:
Finalmente, el área de la región es: A = A1 + A2
y de allí se obtiene A2 = 64/3
A =
2
m
33
,
33
3
100
A 

Solución d) del Ejemplo 3

27. Elaborado por Elsa Guédez
Ejemplo 4
Se ha determinado que “t” meses después de iniciado el
proceso de explotación controlado del sembradío, éste se
habrá desforestado a razón de:
Un ingenio azucarero del país controla un sembradío de caña
de azúcar cuyo perímetro corresponde a la región limitada
por las gráficas de

28. Elaborado por Elsa Guédez
Ejemplo 4
b) Determinar el valor de la constante “b” de modo que a los 2
meses de iniciado el proceso de explotación controlado
referido, se haya desforestado la mitad del sembradío.
a) Determinar el área de la zona correspondiente al sembradío.

29. Elaborado por Elsa Guédez
Solución Ejemplo 4
A continuación se muestra el gráfico donde se representa la zona
poblada
Parte (a)

30. Elaborado por Elsa Guédez
Solución a) del Ejemplo 4
Se tiene: , de allí: x= 4 – y2  H(y) = 4 - y2
Asimismo: x = 2y + y2 , de allí: G(y) = 2y + y2
Se considerará:
La partición de “n” subintervalos para t∈ [-2, 0]
Ancho de cada subintervalo: ∆y.
Puntos muestra: yi
* (Puntos medios de c/subintervalo – optativo)
Por lo cual, el área del rectángulo # i es:

31. Elaborado por Elsa Guédez
Que equivale a:
Y el área “A” de la región es:
Solución a) del Ejemplo 4

32. Elaborado por Elsa Guédez
Dada la continuidad de la función integrando, es posible la
aplicación del Teorema fundamental del Cálculo y calcular el
área “A1”.
Conclusión:
El área del sembradío es: 6,66 Km2.
= 20/3
Solución a) del Ejemplo 4

33. Elaborado por Elsa Guédez
Solución b) del Ejemplo 4
Se considerará:
La partición de “n” subintervalos para t∈ [-2, 0]
Ancho de cada subintervalo: ∆t.
Puntos muestra: ti
* (Puntos medios de c/subintervalo – optativo)
Asumiendo constante a F(t) en cada subintervalo y dada por su
valor en el punto muestra correspondiente de modo que, la
cantidad de sembradío desforestado durante el subintervalo # i
es:
Δt
)
t
F(
L *
i
i 

34. Elaborado por Elsa Guédez
Que equivale a:
Por lo tanto, la cantidad de sembradío desforestado durante 2
meses, que debe corresponder a la mitad del área total 20/3 Km2,
cumple con la igualdad:
Solución b) del Ejemplo 4

35. Elaborado por Elsa Guédez
Dada la continuidad de la función integrando, es posible la
aplicación del Teorema fundamental del Cálculo:
Haciendo el cambio de variable u = 0,5b – t4 , se obtiene
que la integral indefinida es igual a:
Para la integral indefinida:
Solución b) del Ejemplo 4

36. Elaborado por Elsa Guédez
En consecuencia:
De allí, se obtiene:
Sustituyendo (2) en (1), resulta:
Solución b) del Ejemplo 4
Conclusión
El valor de la constante “b” deberá ser alrededor de 5,18 para que
se cumpla lo especificado.