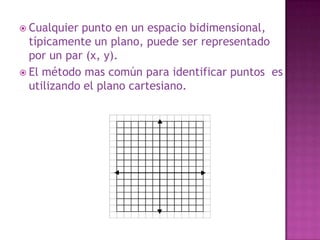
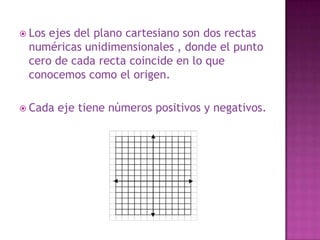
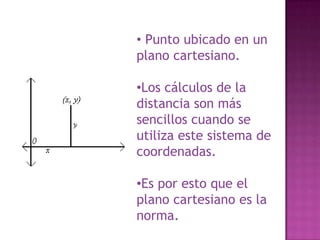
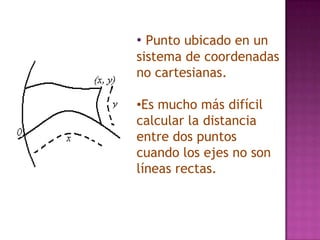
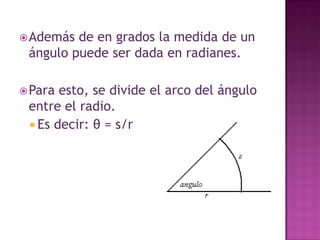
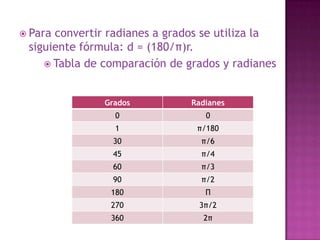
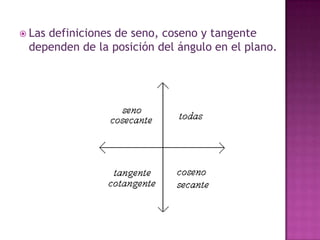
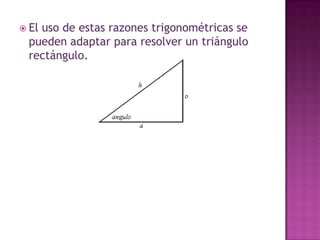
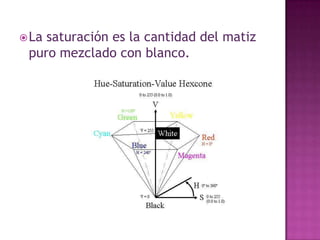
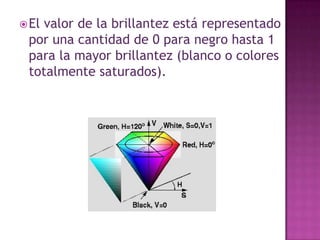
El documento discute diferentes sistemas de coordenadas para representar puntos en espacios de una, dos y tres dimensiones, incluyendo coordenadas cartesianas y polares. También describe métodos para representar y medir color, como la adición de componentes rojo, verde y azul o matiz, saturación y valor.

1. Coordenadas y dimensión: Representaciones del espacio y colorAmbar OliverasJoane M. De JesúsMatemática Discreta Avanzada14 de enero de 2010

2. En esta presentación se discutirán maneras de definir, medir y controlar espacios de una o varias dimensiones. También se discutirán las diferentes interpretaciones de color.

3. Coordenadas cartesianasLos números reales pueden representarse en la recta numérica.Cada punto representa un número y viceversa.Un intervalo es un rango de valores ininterrumpidos representados en la recta.

4. Un intervalo cerrado tiene dos fronteras y se escribe de la forma [a, b]. En notación de conjunto se escribe {x: a ≤ x ≤ b}Un intervalo abierto no tiene fronteras y se escribe de la forma (a, b) o ]a, b[.En notación de conjunto se escribe {x: a < x< b}

5. Un intervalo semi-abierto tiene una sola frontera y se escribe de la forma [a, b) o (a, b].Los puntos en dos dimensiones tienen una relación uno-a-uno y completa con pares ordenados de números reales.

6. Cualquier punto en un espacio bidimensional, típicamente un plano, puede ser representado por un par (x, y).El método mas común para identificar puntos es utilizando el plano cartesiano.

7. Los ejes del plano cartesiano son dos rectas numéricas unidimensionales , donde el punto cero de cada recta coincide en lo que conocemos como el origen.Cada eje tiene números positivos y negativos.

8. Las unidades de los ejes del plano cartesiano pueden ser diferentes, cuando esto sucede y deseamos comparar dos figuras, debemos ser capaces de convertir una de las unidades en la otra.Los puntos en el plano pueden ser definidos respecto a dos rectas numéricas cualquiera con un ángulo mayor de cero entre ellas.

9. Punto ubicado en un plano cartesiano.

10. Los cálculos de la distancia son más sencillos cuando se utiliza este sistema de coordenadas.

11. Es por esto que el plano cartesiano es la norma.Punto ubicado en un sistema de coordenadas no cartesianas.

12. Es mucho más difícil calcular la distancia entre dos puntos cuando los ejes no son líneas rectas.Sin embargo este es el sistema de coordenadas que utilizamos cuando vemos un mapa del mundo.

13. Al utilizar este sistema se presentan dificultades en la interpretación de la distancia más corta entre dos puntos en el globo.Esto sucede dado que la misma es un arco en vez de una línea recta como normalmente se espera.Utilizar un triángulo rectángulo en el plano cartesiano hace que calcular la distancia entre dos puntos sea relativamente más fácil.

14. El teorema de Pitágoras establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.Es decir: a² + b² = c²De este teorema podemos derivar la fórmula de la distancia: d = √{(x₂ - x₁)² + (y₂ - y₁)²}

15. ecuaciones y desigualdadesLa relación entre los valores de x y y expresada como una ecuación puede ser representada como una curva conocida como “locus”.Una manera de establecer la forma de una ecuación es graficando varios valores de y para valores dados de x, asumiendo que los puntos se conectan.

16. En varios casos, la gráfica se comporta de la manera que esperamos, pero en otros, nuestras inferencias no resultan válidas al observar el sistema.Así como las desigualdades en la recta numérica representan intervalos, las desigualdades en un espacio de dos dimensiones representan regiones de este espacio.

17. ÁngulosUn ángulo representa un cambio en dirección.Los conceptos sobre ángulos más conocidos son que un ángulo recto mide 90° y que una revolución son 360 °.El viaje que realiza la Tierra alrededor del Sol en un día representa un grado.

18. Además de en grados la medida de un ángulo puede ser dada en radianes.Para esto, se divide el arco del ángulo entre el radio.Es decir: θ = s/r

19. Usando la fórmula de la circunferencia C = 2πr, podemosinferirqueunarevoluciónesigual a 2πradianes.Los valores de los ángulos más conocidos en radianes están en términos de π.Para convertir grados a radianes se utiliza la siguiente fórmula: r = (π/180)d.

20. Para convertir radianes a grados se utiliza la siguiente fórmula: d = (180/π)r.Tabla de comparación de grados y radianes

21. Un ángulo con una medida de un radian es un poco más pequeño que 60°.Un radian es 180/π=57.3° aproximadamente.Es importante recordar que la fórmulas que utilizamos en computadora son ángulos expresados en radianes.

22. Trigonometría y coordenadas polaresLas coordenadas cartesianas son muy útiles, pero no son el único sistema utilizado.Un punto expresado en coordenadas cartesianas (x, y) puede ser representado en coordenadas polares (r, θ).r es la distanciadesde el origenhasta el puntoθes el ángulo

23. ConversiónPara convertir coordenadas cartesianas a polares se utilizan las siguientes fórmulas: x = r cos(θ) y = r sin(θ)Para convertir coordenadas cartesianas a polares utilizamos funciones trigonométricas.sin(θ)=y/rcos(θ)=x/rtan(θ)=y/x; donde x≠0

24. Las definiciones de seno, coseno y tangente dependen de la posición del ángulo en el plano.

25. El uso de estas razones trigonométricas se pueden adaptar para resolver un triángulo rectángulo.

26. Usando triángulos rectángulos especiales, se hallaron los valores de seno, coseno y tangente para los ángulos más comunes.

27. Otra manera para convertir coordenadas cartesianas a polares depende del teorema de Pitágoras, donde la hipotenusa r=√(x²+y²) y el ángulo es θ = arctan(y/x).Para calcular la medida de los lados y de los ángulos de cualquiertipo de triángulo se utilizanlasleyes de seno y coseno. a² = b² + c² - 2bc cos(A) a/sin(A) = b/sin(B) = c/sin(C)

28. DimensiónEnfoque de separación: Dos puntos distintos pueden ser separados por una figura de menor dimensión a la dimensión total.Enfoque de construcción: Si trasladamos una figura, le añadimos una dimensión.Enfoque de coordenadas: El número mínimo de valores necesarios para identificar un punto indica la dimensión.

29. Sistemas de coordenadas en tres dimensionesEn el sistema de coordenadas Cartesianas en tres dimensiones, la posición de un punto está determinada por un triple ordenado (x, y, z). En este espacio, la distancia es una extensión de la distancia en dos dimensiones derivada del Teorema de Pitágoras.d = √{(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²}

30. Así como una ecuación en dos dimensiones define una línea o curva, una ecuación en tres dimensiones define una superficie o plano.Una desigualdad en tres dimensiones representa una región en el espacio.

31. Los sistemas de coordenadas polares en tres dimensiones más utilizados son las coordenadas cilíndricas y las coordenadas esféricas.Las coordenadas cilíndricas polares de un punto P se representan con las coordenadas P(r, θ, z). Las fórmulas para convertir de cilíndricas polares a cartesianas son iguales a las de dos dimensiones, pero se añade la z.

32. Las coordenadas esféricas polares de un punto P se representan con las coordenadas P(r, θ, φ).r = √(x² + y² + z²)θ = arctan(y/x)φ = arccos(z/r)

33. El color y su representaciónAdición de color (r, g, b)r= red (rojo)g= green (verde)b=blue (azul)Una representación de (0, 0, 0) significa que no se ha añadido ningún color, de modo que esto representa negro.

34. Una representación de (1, 1, 1) representa blanco.Otros colores se pueden obtener asignando valores a cada uno de los componentes de 0 a 255.Ejemplos:Rojo: (1, 0, 0)Verde: (0, 1, 0)Azul: (0, 0, 1)Cyan: (0, 1, 1)Magenta: (1, 0, 1)Amarillo: (1, 1, 0)

35. Saturación de color (h, s, v)h= hue (matiz)s= saturation (saturación) v= value (valor)El matiz se representa como un ángulo: 0 grados para rojo, 60 para amarillo, 120 para verde, 240 para azul.

36. La saturación es la cantidad del matiz puro mezclado con blanco.

37. El valor de la brillantez está representado por una cantidad de 0 para negro hasta 1 para la mayor brillantez (blanco o colores totalmente saturados).