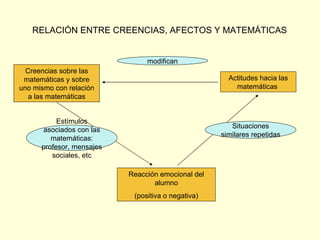
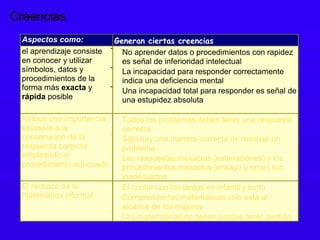
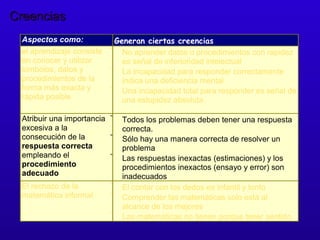
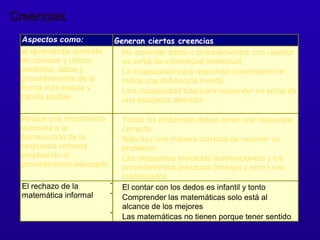
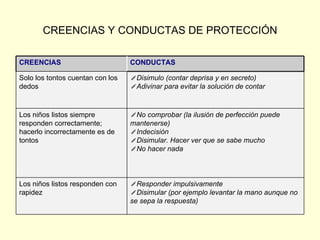
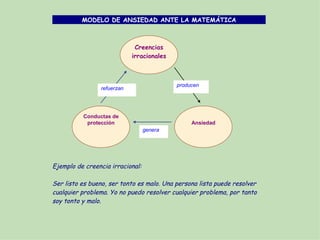
Este documento discute los componentes emocionales del aprendizaje de las matemáticas, incluyendo creencias, actitudes y emociones. Explica que las creencias y actitudes afectan la forma en que los estudiantes aprenden y aplican las matemáticas, y pueden obstaculizar el aprendizaje. También describe cómo fomentar creencias constructivas en los estudiantes valorando el error y mostrando una actitud positiva hacia las matemáticas informales.

1. Componentes emocionales del aprendizaje de las matemáticas

2. CREENCIAS, ACTITUDES Y EMOCIONES Las Creencias, pueden ser de dos tipos: Acerca de las matemáticas como disciplina (poco componente afectivo, pero son parte importante del contexto en que el afecto se desarrolla). Acerca de uno mismo y de su relación con las matemáticas (fuerte componente afectivo), incluyen: Confianza Autoconcepto Atribución de éxitos y fracasos

3. Las Actitudes: Actitudes hacia las matemáticas (hay un predominio del componente afectivo) Interés Satisfacción Curiosidad Valoración Actitudes matemáticas (predominio del componente cognitivo) Flexibilidad de pensamiento Apertura mental Espíritu crítico Objetividad …

4. LOS AFECTOS EN MATEMÁTICAS Emociones, actitudes y creencias Tienen un fuerte impacto en cómo los alumnos aprenden y aplican las matemáticas Influyen en la formación del autoconcepto matemático Interaccionan con el sistema cognitivo Estructuran la realidad social del aula Pueden obstaculizar el aprendizaje

5. RELACIÓN ENTRE CREENCIAS, AFECTOS Y MATEMÁTICAS Creencias sobre las matemáticas y sobre uno mismo con relación a las matemáticas Actitudes hacia las matemáticas Reacción emocional del alumno (positiva o negativa) Estímulos asociados con las matemáticas: profesor, mensajes sociales, etc Situaciones similares repetidas modifican

6. Creencias

7. Creencias

8. Creencias

9. CREENCIAS Y CONDUCTAS DE PROTECCIÓN Responder impulsivamente Disimular (por ejemplo levantar la mano aunque no se sepa la respuesta) Los niños listos responden con rapidez No comprobar (la ilusión de perfección puede mantenerse) Indecisión Disimular. Hacer ver que se sabe mucho No hacer nada Los niños listos siempre responden correctamente; hacerlo incorrectamente es de tontos Disimulo (contar deprisa y en secreto) Adivinar para evitar la solución de contar Solo los tontos cuentan con los dedos CONDUCTAS CREENCIAS

10. FOMENTO DE CREENCIAS CONSTRUCTIVAS No buscar la perfección Valorar el error como parte del proceso Valorar las preguntas Contrarrestar conceptos erróneos como el rechazo del tanteo, de la estimación, de la búsqueda de métodos abreviados, de la existencia de “formas únicas” de resolver un problema, etc. Poner de manifiesto la inexactitud de las creencias perfeccionistas y ayudar a los niños a desarrollar una perspectiva adecuada.

11. FOMENTO DE CREENCIAS CONSTRUCTIVAS Especialmente importante en niños con dificultades de aprendizaje o ansiedad ante las matemáticas. Mostrar una actitud receptiva ante la matemática informal y valorar su utilidad personal e histórica para el desarrollo del conocimiento matemático Fomentar en los niños una imagen positiva de la matemática informal Aplicar el trabajo matemático a situaciones cotidianas para ellos y partir de la forma en intuitivamente las abordan (actividades singulares) Relacionar los materiales nuevos con experiencias familiares para los niños.