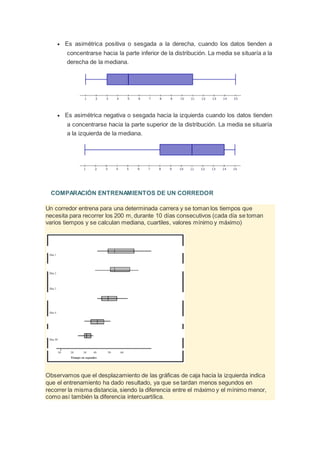
El documento explica el diagrama de cajas y bigotes, el cual resume los valores estadísticos clave de un conjunto de datos como el valor mínimo, primer y tercer cuartil, y máximo. El diagrama consiste en una caja que abarca el rango intercuartílico y bigotes que se extienden desde el primer cuartil hasta el valor mínimo y desde el tercer cuartil hasta el valor máximo. El documento también proporciona un ejemplo de cómo un diagrama de cajas puede usarse para comparar los tiempos de un corredor en diferentes

1. DIAGRAMA DE CAJAS Y BIGOTES.
Para construir el diagrama de caja has de calcular previamente los valores
necesarios para determinarlo: valor mínimo, primer cuartil, mediana, tercer cuartil y
valor máximo.
La mediana está situada justamente en el medio de la distribución: el 50% de los
datos es igual o inferior a la mediana y el otro 50% es igual o superior. Si en vez de
partir la distribución en dos partes, por la mediana, la dividimos en cuatro, los valores
que nos servirán de división se denominan cuartiles. El primer cuartil, que también
suele llamarse cuartil inferior, deja por debajo al 25% de los datos y por encima al
75% restante. A su vez el tercer cuartil, o cuartil superior, deja por debajo al 75% de
los datos y por encima al 25%. Lógicamente el segundo cuartil es la mediana. A la
diferencia entre los valores de los cuartiles se la denomina recorrido intercuartílico y
también es un parámetro importante. Análogamente podemos definir otras medidas
de posición, como los deciles y los percentiles, que surgen cuando partimos la
distribución en 10 o en 100 partes, respectivamente.
Un diagrama de caja, también llamado diagrama de caja y bigotes, está formado por
un rectángulo, la caja, y dos segmentos, los bigotes, uno a cada lado del rectángulo.
La caja abarca el recorrido intercuartílico, que es el intervalo comprendido entre el
primer cuartil q1 y el tercer cuartil q3. Dentro de la caja se representa con un
segmento la mediana de la distribución. El bigote izquierdo queda determinado por el
valor mínimo y el primer cuartil y el derecho por el tercer cuartil y el valor máximo,
excepto si existen valores atípicos.
 Es simétrica cuando la media, mediana y moda de la distribución coinciden y
los datos se distribuyen de igual forma a ambos lados de esas medidas.

2.  Es asimétrica positiva o sesgada a la derecha, cuando los datos tienden a
concentrarse hacia la parte inferior de la distribución. La media se situaría a la
derecha de la mediana.
 Es asimétrica negativa o sesgada hacia la izquierda cuando los datos tienden
a concentrarse hacia la parte superior de la distribución. La media se situaría
a la izquierda de la mediana.
COMPARACIÓN ENTRENAMIENTOS DE UN CORREDOR
Un corredor entrena para una determinada carrera y se toman los tiempos que
necesita para recorrer los 200 m, durante 10 días consecutivos (cada día se toman
varios tiempos y se calculan mediana, cuartiles, valores mínimo y máximo)
Observamos que el desplazamiento de las gráficas de caja hacia la izquierda indica
que el entrenamiento ha dado resultado, ya que se tardan menos segundos en
recorrer la misma distancia, siendo la diferencia entre el máximo y el mínimo menor,
como así también la diferencia intercuartílica.