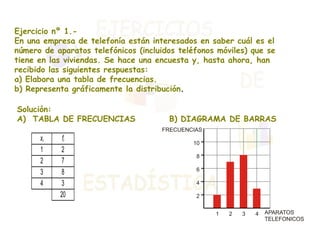
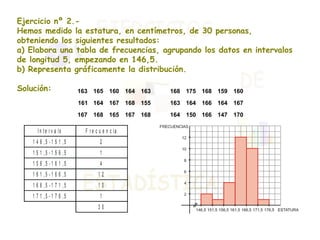
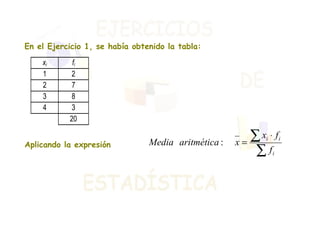
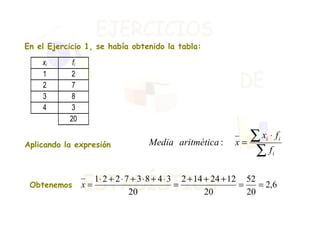
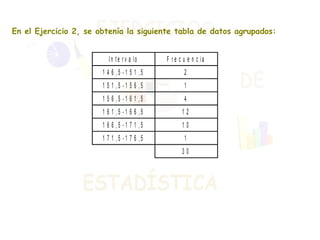
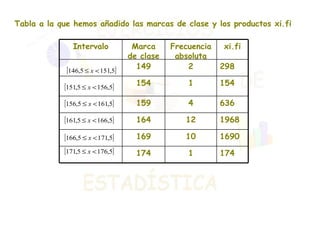
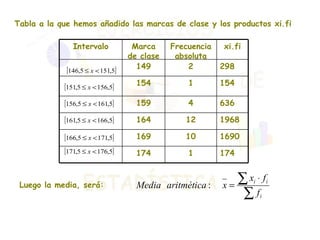
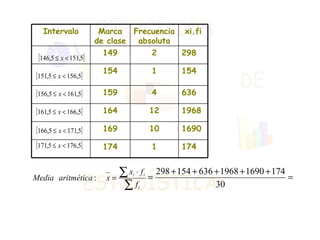
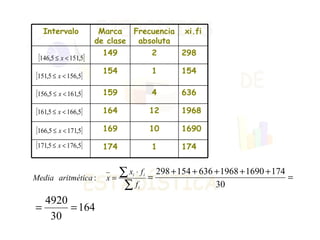
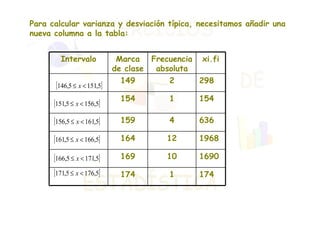
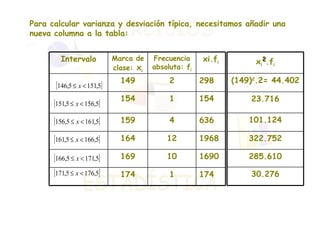
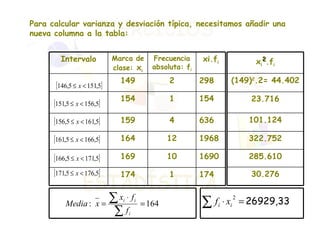
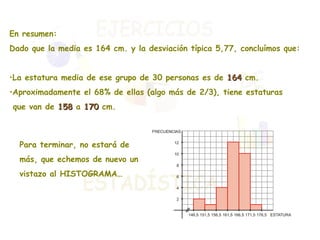
El documento presenta dos ejercicios sobre análisis estadístico: el primero consiste en realizar una encuesta sobre el número de teléfonos en las viviendas, donde se deben elaborar tablas de frecuencias y gráficos; el segundo ejercicio trata de la estatura de 30 personas, que también requiere crear tablas y representar gráficamente los resultados. Se calcula la media aritmética y los parámetros de dispersión (varianza y desviación típica) para aportar información sobre la concentración de los datos. Finalmente, se concluye que la estatura media es de 164 cm y que aproximadamente el 68% de las personas se encuentra entre 158 y 170 cm.

2. Ejercicio nº 1 En una empresa de telefonía están interesados en saber cuál es el número de aparatos telefónicos (incluidos teléfonos móviles) que se tiene en las viviendas. Se hace una encuesta y, hasta ahora, han recibido las siguientes respuestas: a) Elabora una tabla de frecuencias. b) Representa gráficamente la distribución.

3. Ejercicio nº 1.- En una empresa de telefonía están interesados en saber cuál es el número de aparatos telefónicos (incluidos teléfonos móviles) que se tiene en las viviendas. Se hace una encuesta y, hasta ahora, han recibido las siguientes respuestas: a) Elabora una tabla de frecuencias. b) Representa gráficamente la distribución . Solución: A) TABLA DE FRECUENCIAS B) DIAGRAMA DE BARRAS

4. Ejercicio nº 2.- Hemos medido la estatura, en centímetros, de 30 personas, obteniendo los siguientes resultados: a) Elabora una tabla de frecuencias, agrupando los datos en intervalos de longitud 5, empezando en 146,5. b) Representa gráficamente la distribución.

5. Ejercicio nº 2.- Hemos medido la estatura, en centímetros, de 30 personas, obteniendo los siguientes resultados: a) Elabora una tabla de frecuencias, agrupando los datos en intervalos de longitud 5, empezando en 146,5. b) Representa gráficamente la distribución. Solución:

6. Cálculo de la media aritmética

7. Cálculo de la media aritmética Se calcula mediante la expresión:

8. Cálculo de la media aritmética Se calcula mediante la expresión: Donde son los valores de los datos estadísticos y son las frecuencias absolutas .

9. En el Ejercicio 1, se había obtenido la tabla:

10. En el Ejercicio 1, se había obtenido la tabla: Aplicando la expresión

11. En el Ejercicio 1, se había obtenido la tabla: Aplicando la expresión Obtenemos

12. En el Ejercicio 2, se obtenía la siguiente tabla de datos agrupados:

13. Tabla a la que hemos añadido las marcas de clase y los productos xi.fi 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.fi Frecuencia absoluta Marca de clase Intervalo

14. Tabla a la que hemos añadido las marcas de clase y los productos xi.fi Luego la media, será: 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.fi Frecuencia absoluta Marca de clase Intervalo

15. 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.fi Frecuencia absoluta Marca de clase Intervalo

16. 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.fi Frecuencia absoluta Marca de clase Intervalo

17. PARÁMETROS DE DISPERSIÓN Los parámetros de dispersión ( varianza y desviación típica principalmente) nos indican el grado de concentración de los datos respecto a la media.

18. PARÁMETROS DE DISPERSIÓN Los parámetros de dispersión ( varianza y desviación típica principalmente) nos indican el grado de concentración de los datos respecto a la media. Las fórmulas son: Varianza: Desviación típica:

19. Para calcular varianza y desviación típica, necesitamos añadir una nueva columna a la tabla: 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.fi Frecuencia absoluta Marca de clase Intervalo

20. Para calcular varianza y desviación típica, necesitamos añadir una nueva columna a la tabla: 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.f i Frecuencia absoluta: f i Marca de clase: x i Intervalo 30.276 285.610 322.752 101.124 23.716 (149) 2 .2= 44.402 x i 2 .f i

21. Para calcular varianza y desviación típica, necesitamos añadir una nueva columna a la tabla: 174 1 174 1690 10 169 1968 12 164 636 4 159 154 1 154 298 2 149 xi.f i Frecuencia absoluta: f i Marca de clase: x i Intervalo 30.276 285.610 322.752 101.124 23.716 (149) 2 .2= 44.402 x i 2 .f i

22. FINALMENTE: Varianza: Desviación típica:

23. Es importante saber que la MEDIA ARITMÉTICA y la DESVIACIÓN TÍPICA, tienen una relación muy interesante…

24. Es importante saber que la MEDIA ARITMÉTICA y la DESVIACIÓN TÍPICA, tienen una relación muy interesante… El intervalo contiene aproximadamente el 68% de los datos El intervalo aproximadamente el 95% El intervalo aproximadamente el 98%

25. En este ejemplo podríamos decir que: El 68% de los datos está comprendido entre (164-5,77 y 164+5,77), es decir: El 68% de los datos está entre 158,23 y 169,77

26. En resumen: Dado que la media es 164 cm . y la desviación típica 5,77 concluímos que: La estatura media de ese grupo de 30 personas es de 164 cm. Aproximadamente el 68% de ellas (algo más de 2/3), tiene estaturas que van de 158 a 170 cm. Para terminar, no estará de más, que echemos de nuevo un vistazo al HISTOGRAMA…

27. En resumen: Dado que la media es 164 cm. y la desviación típica 5,77, concluímos que: La estatura media de ese grupo de 30 personas es de 164 cm. Aproximadamente el 68% de ellas (algo más de 2/3), tiene estaturas que van de 158 a 170 cm. Para terminar, no estará de más, que echemos de nuevo un vistazo al HISTOGRAMA…