estadistica unidimensional
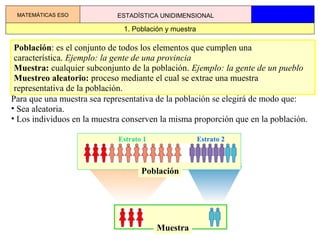
- 1. Muestra Población: es el conjunto de todos los elementos que cumplen una característica. Ejemplo: la gente de una provincia Muestra: cualquier subconjunto de la población. Ejemplo: la gente de un pueblo Muestreo aleatorio: proceso mediante el cual se extrae una muestra representativa de la población. Población Estrato 1 Estrato 2 Para que una muestra sea representativa de la población se elegirá de modo que: • Sea aleatoria. • Los individuos en la muestra conserven la misma proporción que en la población. 1. Población y muestra MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 2. Variable o carácter estadístico: es una propiedad que permite clasificar a los individuos de la población. Ejemplos: deporte practicado, número de hermanos, peso. Caracteres estadísticos Cualitativos Cuantitativos : no se pueden medir. Ej: deporte se pueden medir. Ejemplos: nº de hermanos, peso Dentro de él se pueden establecer modalidades. Ejemplo: fútbol, baloncesto,… 2. caracteres estadísticos MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL Discretos Continuos: : toma valores aislados. Ej: nº de hermanos puede tomar infinitos valores Ej: peso
- 3. • En caso de que la variable sea continua, o discreta con un número de datos muy grande, resulta aconsejable agrupar los datos en intervalos (clases). • El punto medio de cada clase recibe el nombre de marca de clase. • Los intervalos se deben hacer de manera que el extremo superior de cada clase coincida con el extremo inferior de la siguiente. Se han anotado las tallas en cm de los 36 alumnos de una clase. Se han obtenido: 168, 168, 159, 160, 163, 156, 164, 160, 164, 171, 169, 166, 169, 163, 160, 154, 174, 165, 161, 162, 157, 170, 166, 164, 162, 157, 158, 170, 159, 172, 167, 161, 178, 169, 177, 169. Al agrupar los datos en 6 intervalos de amplitud 5 cm se obtuvo: 3. Intervalos. Marca de clases y tabla de frecuencia MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL Talla en cm. Recuento Marcas de clase Número de alumnos [150–155) / 152,5 1 [155–160) ////// 157,5 6 [160–165) //////////// 162,5 12 [165–170) ////////// 167,5 10 [170–175) ///// 172,5 5 [175–180) // 177,5 2
- 4. • Frecuencia absoluta (fi ó ni) del valor xi: es el número de veces que se repite ese valor. • Frecuencia relativa (hi) del valor xi: es el cociente entre la frecuencia absoluta de xi y el número total de datos que intervienen en la distribución. Clases Marcas xi Frecuencia absoluta fi Frecuencia relativa hi [150–155) 152,5 1 1 1 6 [155–160) 157,5 6 6 1 6 [160–165) 162,5 12 1 2 1 6 [165–170) 167,5 10 1 0 1 6 [170–175) 172,5 5 5 1 6 [175–180) 177,5 2 2 1 6 4. Tablas de frecuencias absolutas y relativas MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 5. • Frecuencia absoluta acumulada (Fi ó Ni) del valor xi: es la suma de las frecuencias absolutas de los valores anteriores o iguales a xi. • Frecuencia relativa acumulada (Hi) del valor xi: es la suma de las frecuencias absolutas relativas de los valores anteriores o iguales a xi. Clases Marcas xi Frecuencia absoluta fi Frecuencia relativa hi Frecuencia absoluta acumulada Fi Frecuencia relativa acumulada Hi [150–155) 152,5 1 1 1 6 1 1 1 6 [155–160) 157,5 6 6 1 6 7 7 1 6 [160–165) 162,5 12 1 2 1 6 19 1 9 1 6 [165–170) 167,5 10 1 0 1 6 29 2 9 1 6 [170–175) 172,5 5 5 1 6 34 3 4 1 6 [175–180) 177,5 2 2 1 6 36 1 5. Tablas de frecuencias absolutas y relativas acumuladas MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 6. 6. Porcentajes MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL Clases Marcas xi Frecuenci a absoluta fi Frecuencia relativa hi Frecuencia absoluta acumulada Fi Frecuencia relativa acumulada Hi Porcentajes pi = Porcentajes acumulados Pi = [150–155) 152,5 1 0,028 1 0,028 2 2 [155–160) 157,5 6 0,17 7 0.198 17 19 [160–165) 162,5 12 0,33 19 0,528 33 52 [165–170) 167,5 10 0,28 29 0,806 28 80 [170–175) 172,5 5 0,14 34 0,944 14 94 [175–180) 177,5 2 0,056 36 1 5 100 • Frecuencia porcentual (pi) del valor xi: es igual a la frecuencia relativa por 100. pi =100*hi • Frecuencia porcentual acumulada (Pi) del valor xi: es igual a la frecuencia relativa acumulada por 100. Pi =100*Hi
- 7. • Se utilizan para comparar las modalidades de un carácter mediante sectores circulares. • El ángulo central de un sector ha de ser proporcional a la frecuencia absoluta correspondiente. ¿Qué importancia le das a tu trabajo? ¿Qué importancia le das a tu tiempo libre? 7. Diagrama de sectores MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 8. 8. Diagrama de barras MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL Se utilizan para comparar datos cualitativos o cuantitativos discretos. En el eje horizontal se sitúan las modalidades, y en el vertical sus frecuencias absolutas o relativas.
- 9. Se utilizan para distribuciones de variables estadísticas continuas o para distribuciones de variables estadísticas discretas con un gran número de datos y agrupados en clases. 9. Histograma y polígono de frecuencias MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 10. La moda es la modalidad o el valor que más se repite, es decir, el de mayor frecuencia absoluta. Para calcular la moda de una variable estadística agrupada en clases se toma como valor aproximado de la moda la marca de la clase que presenta mayor frecuencia absoluta. Esta clase se llama clase modal. Clases Marcas xi Frecuencia absoluta fi [150–155) 152,5 1 [155–160) 157,5 6 [160–165) 162,5 12 [165–170) 167,5 10 [170–175) 172,5 5 [175–180) 177,5 2 36 Mo = 162,5 cm 10. Parámetros de centralización. Moda MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 11. La media aritmética es la suma de todos los valores dividida por el número total de valores. Cada valor ( xi ) se tiene en cuenta tantas veces como aparezca (fi ) i i i i1 1 2 2 n n 1 2 n i x f x fx f x f ... x f x f f ... f f N + + + = = = + + + ∑ ∑ ∑ Clases Marcas xi Frecuencia absoluta fi xi fi [150–155) 152,5 1 152,5 [155–160) 157,5 6 945 [160–165) 162,5 12 1950 [165–170) 167,5 10 1675 [170–175) 172,5 5 862,5 [175–180) 177,5 2 355 36 5940 5940 x 165 cm 36 = = 11. Parámetros de centralización. Media MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 12. • La mediana separa los datos ordenados de menor a mayor en dos intervalos con el mismo número de datos. Ej: 1,1,1,2,2,2,4,5,5,5,6. Mediana = 2 • Si los datos están agrupados, el intervalo o clase mediana es el primer intervalo cuya frecuencia absoluta acumulada es mayor que la mitad del número de datos y la mediana es la marca de la clase mediana. Clases Marcas xi Frecuencia absoluta fi Frecuencia absoluta acumulada Fi [150–155) 152,5 1 1 [155–160) 157,5 6 7 < 18 [160–165) 162,5 12 19 > 18 [165–170) 167,5 10 29 [170–175) 172,5 5 34 [175–180) 177,5 2 36 M = 162,5 cm 12. Parámetros de centralización. Mediana MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 13. Los cuartiles separan los datos en cuatro grupos de la manera siguiente: 1 1 2 2 2 3 3 3 3 4 4 4 4 4 5 5 5 6 6 7 7 7 7 8 9 9 Q1 Q2 Q3 xi fi Fi Hi 1 2 2 0,08 2 3 5 0,19 3 4 9 0,35 4 5 14 0,54 5 3 17 0,65 6 2 19 0,73 7 4 23 0,88 8 1 24 0,92 9 2 26 1 Q1: es el primer valor que supera a la cuarta parte de los datos Q2: es el valor de la mediana Q3: es el primer valor que supera a las tres cuartas partes de los datos 13. Cuartiles MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 14. Se llama recorrido de una variable estadística a la diferencia entre su valor máximo y su valor mínimo. R = MAX – MIN. Ej: R = 177,5 – 152,5 = 15. Se llama desviación media de una variable estadística X a la media aritmética de los valores absolutos de las desviaciones respecto a la media. i i i i i f | x x | f | x x | DM f N − − = = ∑ ∑ ∑ Clases Marcas xi Frecuencia absoluta fi xi – | xi – | fi | xi – | [150–155) 152,5 1 –12,5 12,5 12,50 [155–160) 157,5 6 –7,5 7,5 45,00 [160–165) 162,5 12 –2,5 2,5 30,00 [165–170) 167,5 10 2,5 2,5 25,00 [170–175) 172,5 5 7,5 7,5 37,00 [175–180) 177,5 2 12,5 12,5 25,00 36 175,00 175 DM 4,86 cm 36 = = 14. Parámetros de dispersión. Recorrido o rango. Desviación media MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 15. Se llama varianza de la variable estadística X a la media aritmética de los cuadrados de las desviaciones respecto de la media. A su raíz cuadrada se le llama desviación típica. 2 2 i i i i2 2 i i f (x x) f x s x f f − = = − ∑ ∑ ∑ ∑ Clases Marcas xi Frecuencia absoluta fi xi 2 fi xi 2 [150–155) 152,5 1 23256 23256 [155–160) 157,5 6 24804 148838 [160–165) 162,5 12 26406 316875 [165–170) 167,5 10 28056 280563 [170–175) 172,5 5 29756 148781 [175–180) 177,5 2 31506 63013 36 981325 2 2 i i i i 2 i i f (x x) f x s x f f − = = − ∑ ∑ ∑ ∑ 2 i i2 2 i 2 2 f x s x f 981325 165 34,03 cm 36 = − = = − = ∑ ∑ s 34,03 5,83 cm= = 15. Parámetros de dispersión. Varianza y desviación típica MATEMÁTICAS ESO ESTADÍSTICA UNIDIMENSIONAL
- 16. En distribuciones unimodales y bastante simétricas se verifica que: • En el intervalo se encuentra aproximadamente el 68% de los datos. • En el intervalo se encuentra aproximadamente el 95% de los datos. • En el intervalo se encuentra aproximadamente el 99% de los datos. (x s, x s)− + (x 2s, x 2s)− + (x 3s, x 3s)− + 68% 95% 99% 16. Distribución de los datos respecto a la media MATEMÁTICAS 4 ESO ESTADÍSTICA UNIDIMENSIONAL