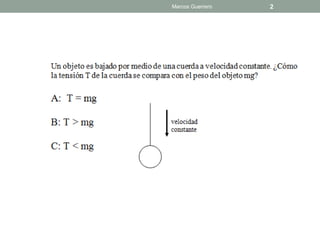
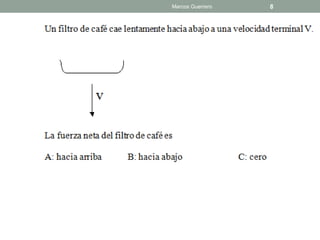
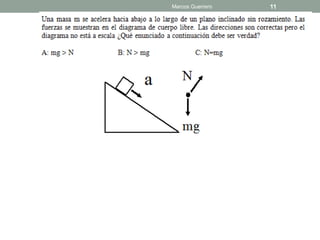
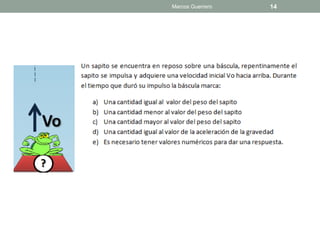
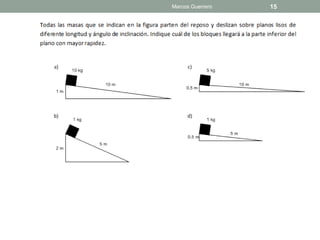
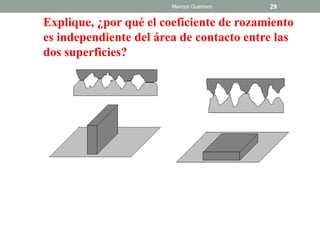
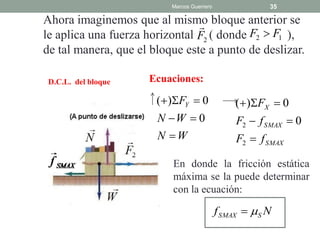
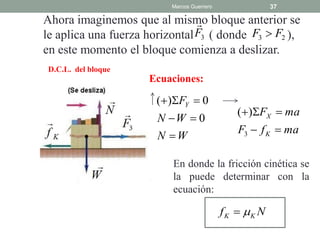
El documento repasa las leyes de Newton y la fricción. Explica el coeficiente de rozamiento estático y cinético, y cómo la fuerza de fricción depende de la fuerza normal y el coeficiente. También analiza casos donde un bloque está en reposo, a punto de deslizarse o deslizándose, y describe cómo cambia la fuerza de fricción.

1. Marcos Guerrero 1
Repaso de las Leyes de Newton

2. Marcos Guerrero 2

3. Marcos Guerrero 3

4. Marcos Guerrero 4

5. Marcos Guerrero 5

6. Marcos Guerrero 6

7. Marcos Guerrero 7

8. Marcos Guerrero 8

9. Marcos Guerrero 9

10. Marcos Guerrero 10

11. Marcos Guerrero 11

12. Marcos Guerrero 12

13. Marcos Guerrero 13

14. Marcos Guerrero 14

15. Marcos Guerrero 15

16. Marcos Guerrero 16

17. Marcos Guerrero 17

18. Marcos Guerrero 18

19. Marcos Guerrero 19

20. Marcos Guerrero 20

21. Marcos Guerrero 21

22. Marcos Guerrero 22

23. Marcos Guerrero 23

24. Marcos Guerrero 24

25. Marcos Guerrero 25

26. Marcos Guerrero 26
Aplicaciones de las Leyes
de Newton con Fricción
Por Marcos Guerrero

27. Marcos Guerrero 27
Coeficiente de rozamiento ( )
También llamado coeficiente de fricción.
Es un número adimensional (sin unidades) que mide las
rugosidades entre las dos superficies sólidas en contacto.

28. Marcos Guerrero 28
El coeficiente de rozamiento depende de los siguientes
factores:
•Del material de los cuerpos en contacto (por ejemplo
cobre y madera; madera y vidrio etc.)
•De la interfase (polvo; aceite; agua; etc.)
•De la velocidad con la cual se desliza un cuerpo respecto
al otro (velocidad relativa).
•De la lisura de las superficies.
•De la temperatura.
•Otras variables.
Es independiente del área de contactos.

29. Marcos Guerrero 29
Explique, ¿por qué el coeficiente de rozamiento
es independiente del área de contacto entre las
dos superficies?

30. Marcos Guerrero 30
Existen dos tipos de coeficiente de rozamiento, estos son:
•Coeficiente de rozamiento estático ( S ).
•Coeficiente de rozamiento cinético (  K ) o coeficiente de
rozamiento dinámico.
Por lo general S  K

31. Marcos Guerrero 31

Fuerza de rozamiento ( f)
También llamado fuerza de fricción.
La magnitud de la fuerza de rozamiento es
proporcional a la magnitud de la fuerza de la
normal .
f N
Para llevar esta proporcionalidad a una ecuación,
incluimos una constante. Esta constante es el
coeficiente de rozamiento.
f  N
Llevando esta ecuación en forma vectorial
tenemos:
ˆ
f   Ni

32. Marcos Guerrero 32
En la ecuación anterior ¿podemos decir que la
fuerza de fricción y la fuerza de la normal tienen
la misma dirección?
Por ejemplo: un bloque sobre una superficie
horizontal con rozamiento, es empujado por una
persona hacia la derecha con una aceleración
constante.
D.C.L. del bloque

a  cons tan te 
F

fK 
W

N

33. Marcos Guerrero 33
Imaginemos que un bloque se encuentra en reposo
sobre una superficie horizontal.
D.C.L. del bloque
Ecuaciones:
( )FY  0
N W  0
N W
No existe fuerza de rozamiento
porque no hay una fuerza
horizontal que intente deslizar
el bloque.

34. Marcos Guerrero 34
Ahora imaginemos que al mismo bloque anterior se

le aplica una pequeña fuerza horizontal F1 , de tal
manera, que el bloque no desliza.
D.C.L. del bloque Ecuaciones:
( )FY  0 ()FX  0
N W  0 F1  f S  0
N W f S  F1
Podemos observar que la
fuerza de fricción estática es
directamente proporcional a la
fuerza aplicada sobre el bloque.

35. Marcos Guerrero 35
Ahora imaginemos que al mismo bloque anterior se

le aplica una fuerza horizontal F2 ( donde F2  F1 ),
de tal manera, que el bloque este a punto de deslizar.
D.C.L. del bloque Ecuaciones:
( )FY  0 ()FX  0
N W  0 F2  f SMAX  0
N W F2  f SMAX
En donde la fricción estática
máxima se la puede determinar
con la ecuación:
f SMAX   S N

36. Marcos Guerrero 36
A partir de la ecuación de fricción estática máxima
podemos definir el coeficiente de rozamiento estático.
Definición del coeficiente de rozamiento estático:
f SMAX
S 
N

37. Marcos Guerrero 37
Ahora imaginemos que al mismo bloque anterior se

le aplica una fuerza horizontal F3 ( donde F3  F2 ),
en este momento el bloque comienza a deslizar.
D.C.L. del bloque
Ecuaciones:
( )FY  0
()FX  ma
N W  0
F3  f K  ma
N W
En donde la fricción cinética se
la puede determinar con la
ecuación:
f K  K N

38. Marcos Guerrero 38
A partir de la ecuación de fricción cinética podemos
definir el coeficiente de rozamiento cinético.
Definición del coeficiente de rozamiento cinético:
fK
K 
N

39. Marcos Guerrero 39
Gráfico fuerza de rozamiento vs. fuerza aplicada.

40. Marcos Guerrero 40
Conclusiones de la gráfica:
o La dirección de la fuerza de fricción estática se opone al
posible deslizamiento.
o La fuerza de fricción estática es mayor o igual a cero y
menor o igual que la fuerza de fricción estática máxima.
0  f S  f SMAX
0  f S  S N
o La dirección de la fuerza de fricción cinética se opone al
deslizamiento.
o La fuerza de fricción cinética es menor a la fuerza de
fricción estática máxima.
f K  f SMAX
K N  S N
K  S

41. Marcos Guerrero 41

42. Marcos Guerrero 42

43. Marcos Guerrero 43

44. Marcos Guerrero 44

45. Marcos Guerrero 45

46. Marcos Guerrero 46

47. Marcos Guerrero 47

48. Marcos Guerrero 48