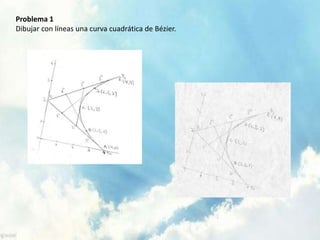
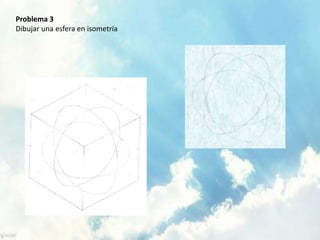
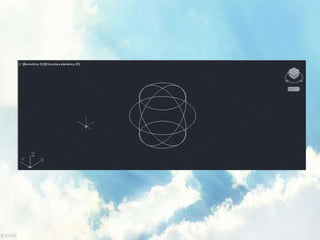
Este documento trata sobre conceptos geométricos de curvas. Explica que una curva es una sucesión continua de puntos sin saltos. Luego describe curvas de primer grado como líneas rectas y curvas de segundo grado como ecuaciones polinómicas. También define una esfera como una curva de segundo grado y presenta su ecuación. Finalmente, introduce el hiperboloide de un manto y propone cinco problemas para dibujar diferentes curvas.

1. Universidad Nacional
Autónoma de México
Diseño y Comunicación Visual en Línea
Materia: Geometría
Maestro: Heidi Nopal Guerrero
Alumno: Alan Gustavo Rodríguez Botello
Fecha: 09/09/2014

2. Curva
El concepto de curva captura la idea de una sucesión de puntos continua, sin
brincos o sobresaltos, hecha con cualquier criterio de forma redondeada; por
lo tanto, primero siempre tenemos que determinar el criterio de construcción
de la curva. En diseño, sobre todo en la parte creativa y de bocetaje, las
curvas se hacen de manera intuitiva, que tiene más que ver con el estilo
artístico del diseñador que con conceptos geométricos; cuando se trata de
una ilustración cuya reproducción se hará mediante sistemas fotográficos, no
requiere de una normalización en conceptos geométricos, pero si se
reproducirá en máquinas, necesita de las características de: exacto,
meticuloso, en suma científico, y es cuando se tiene que abstraer en
conceptos matemáticos como centro, radio, tangencia, coordenadas, etc.,
compatibles con los fines del diseño y la comunicación visual.

3. Curvas de primer grado
El concepto de línea (una sucesión de puntos) se refiere a cualquier recta o
curva, ya que estas se ajustan en forma de polinomios a puntos.
Empecemos con una ecuación polinómica de primer grado: y=ax+b
Curvas de segundo grado
Si aumentamos el orden de la ecuación a la de un polinomio de segundo
grado, obtenemos:
Y=ax^2 + bx + c

4. Problema 1
Dibujar con líneas una curva cuadrática de Bézier.

5. Esfera
Decimos que una esfera es una curva de segundo grado porque uno de los polinomios
más sencillos para generala en un sistema de coordenadas cartesianas en un espacio
euclídeo tridimensional. La ecuación de segundo grado de la esfera unitaria (de radio
1), con centro en el origen, es: x^2 + y^2 + z^2 = 1
Una esfera (del griego σφαῖρα, «sfaira») es la superficie formada por todos los puntos
del espacio tales que la distancia (llamada radio) a un punto determinado, denominado
centro, es siempre la misma. Coloquialmente hablado también se refiere al sólido cuyo
volumen se halla contenido en la superficie anterior; con este significado se emplea
específicamente la palabra bola.
La esfera es la figura geométrica que para igual volumen presenta la superficie externa
menor. Esta propiedad es la causa de su omnipresencia en el mundo físico: “en la
superficie de una gota de un líquido inmerso en un ambiente gaseoso o también
líquido (pero con líquidos que no se pueden mezclar), existen fuerzas superficiales que
deformarán la gota hasta encontrar el valor mínimo de tensión en todos los puntos de
la misma, y este mínimo corresponde a una esfera, en ausencia de toda perturbación
exterior

6. Problema 2
Mediante el uso de meridianos, dibujar una esfera en una aplicación de computadora
de ambiente 3D. (Calculando su base de datos)

7. Problema 3
Dibujar una esfera en isometría

9. Secciones de la esfera
La intersección de un plano y una esfera es, siempre, un círculo llamado
paralelo (eventualmente reducido a un punto, cuando el plano es tangente
en los polos). La esfera es la única superficie del espacio que tiene esta
propiedad.
Si el plano pasa por el centro de la esfera, el radio del círculo es el mismo
que el de la esfera, r. En este caso, la circunferencia puede llamarse ecuador.
Si la distancia d entre el plano y el centro es inferior al radio r de la esfera,
entonces el radio de la sección es, aplicando el teorema de Pitágoras.

10. Problema 4
Dibujar una esfera de r=50, mediante circunferencias paralelas a altura de 10, 20,
30,… 90; calcular la posición de los centros y la longitud de los radios

12. Hiperboloide de un manto
Si aumentamos el orden de la ecuación a la de un polinomio de segundo
grado, obtenemos:
El hiperboloide de un manto es una curva de revolución generada por la
rotación de una hipérbola alrededor de uno de sus dos ejes de simetría.
Estas superficies son de dos clases: de una y de dos hojas o mantos cuando
se gira alrededor del eje azul.
La revolución alrededor del eje de simetría rojo da un hiperboloide de un
manto.

13. Problema 5
Dibujar un hiperboloide de un manto.