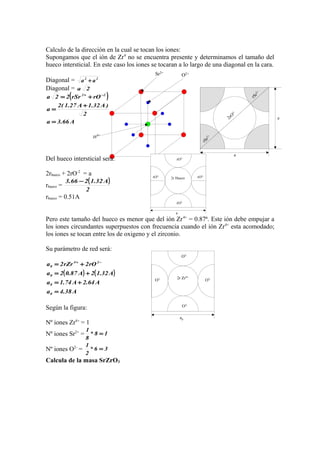
1. La mullita tiene la fórmula 3Al2O3.2SiO2. Contiene un 79.71% de alúmina y un 21.28% de sílice. Se necesitan 85.1076 kg de alúmina para producir 1500 kg de mullita a partir de óxidos puros. 2. El SrZrO3 tiene una estructura perovskita. Los iones se tocan entre los iones de oxígeno y zirconio a lo largo de las diagonales de la cara cúbica. Su parámetro de red es 3.84 Å y

1. LABORATORIO Nº 1 DE CERAMICA Y REFRACTARIOS
1. La mullita como compuesto estequiometrico tiene la siguiente formula:
3Al2O3.2SiO2
a) Cual es el porcentaje en peso de la sílice y alumina en la mullita.
b) Si se prepara una mezcla a partir de oxidos puros para producir mullita
¿Cuál es la cantidad minima de alumina que se necesita para 1500 Kg de
mullita?
a)
3Al2O3.2SiO2 = 3Al2O3 + 2SiO2
Peso molecular de la mullita (3Al2O3.2SiO2) = 426.06024
Cálculo del % en peso del SiO2 Cálculo del % en peso del Al3O2
( )
21.28SiO%
100*
06024.426
)0855.60(2
SiO%
100*
SiO2.OAl3.PM
)SiO.PM(2
SiO%
2
2
2.32
2
2
=
=
=
( )
79.71OAl%
100*
06024.426
)96308.101(3
OAl%
100*
SiO2.OAl3.PM
)OAl.PM(3
OAl%
32
32
232
32
32
=
=
=
b) Tomando 1500 Kg de mullita habrá:
2SiOdeKg15.4231500*
100
21.28
= 32OAldeKg85.10761500*
100
79.71
=
2. En la Wustita (Fe1-xO) que fracción de los lugares vacantes del catión (Fe) estaría
vacante si hubiera iones de Fe3+
por cada 100 iones Fe2+
?
Solución:
Datos
r(Fe2+
) = 0.74 A; r(O2-
) = 1.40A
Se sabe que El FeO tiene una estructura tipo NaCl con NC = 6

2. 2rFe2+
rO2-
rO2-
rO2-
Fe2+
Se dice que por cada 100 Fe2+
hay 10 Fe3+
⇒ 1.0
100
10
Fe
Fe
laciónRe 2
3
=== +
+
Por cada 2 Fe3+
existe una vacancia cationica de Fe2+
entonces:
El Nº de vacancias = 5
2
10
=
El Nº de cationes llenos en la cerámica será:
100Fe2+
+10Fe3+
+5 vacancias = 115 sitios cationicos
Nº de aniones (O2-
) = 115
2
230
= (todos llenos)
La fracción de vacancias cationicas será = 043.0
115
5
=
%Vacancias catiónicas = %3.4100*
115
5
=
La fracción de los sitios llenos será: 1 – 0.043 = 0.942
La formula Fe1-X O = Fe1-0.043 O = Fe0.957O
Calculo de la Masa
nº Fe2+
= 100; nº iones O2-
= 4/celda
nº Fe3+
= 10; nº iones Fe2+
= 4/celda
( ) ( ) ( )
( ) ( ) ( )
g10x33.1mFeO
10x023.6
161155610ºn56100
mFeO
N
.Oxig.A.POºnFe.A.PFeºnFe.A.PFeºn
mFeO
20
23
232
−
−++
=
++
=
++
=
nº de celdas = celdas75.28
celda/O4
115
2
=−
Parametro reticular (a)
a = 2(rFe2+
+ rO2-
)
a = 2(0.74 + 1.4)A
a = 4.28x10-8
cm
Calculo de la Densidad

3. Pb2+ :en el vertice
O2-
:en el centro de las caras
Ti4+
:en el centro del cubo
( )
3
38
20
3
cm/g90.5
celda/cm10x28.4
celdas75.28/10x33.1
celda/a
Celdasºn/mFeO
=
==
−
−
ρ
ρ
3. La densidad del PbTiO3 cúbico es 7.5 g/cm3
¿Cuál es el tamaño de la red de la
celda unitaria. Cual es el factor de empaquetamiento.
Solución:
El PbTiO3 (titanato de Pb) este tipo de cerámica tiene una estructura tipo AmBnXp, la
estructura es del tipo ccc (centrada en las caras) Según la figura:
La estructura tiene coordinación NC = 6 con respecto al O2-
Datos:
r(O2-
) = 1.40 A P.A. =16
Densidad = 7.5 g/cm3
r(Ti4+
) = 0.68 A P.A. = 47.9
r(Pb2+
) = 1.2 A P.A = 207.2
N= 6.023x1023
Primero calculamos el Nº de iones en la celda unitaria
Nº de iones Pb2+
: vértice: 18*
8
1
=
Nº de iones O2-
: en el centro de las caras: 36*
2
1
=
Nº de iones Ti4+
: en el entro del cubo: 1
Sabemos que
v
m
D =
⇒ la masa se calcula como sigue:
( )[ ] ( )[ ] ( )[ ] )1...(
avogradodeºN
atm/gTi.A.PTiºnatm/g.oxig.A.POºnatm/gPb.A.PPbºn
m
422 +−+
++
=
Reemplazando valores en la ecuación (1)
( )[ ] ( )[ ] ( )[ ]
g10x032.5m
10x023.6
atm/g90.471atm/g163atm/g2.2071
m
22
23
−
=
++
=
Calculamos el volumen para calcular “a”
Como sabemos V = a3
⇒ a =
3/1
densidad
m







4. A06.410x406a
cm/g5.7
g10x032.5
a
8
3/1
3
22
==






=
−
Calculo del factor de empaquetamiento
3
3
X
3
A
a
r*
3
4
)(ionesºNr*
3
4
)(ionesºN
unitariacelda.Vol
)(iones.Vol)(iones.Vol
.E.F






−+





+
=
−++
=
ππ
( ) ( ) ( )
( )
%64.E.F
643.0.E.F
A06.4
40.1*
3
4
32.1*
3
4
168.0*
3
4
1
.E.F 3
333
=
=






+





+





=
πππ
4. Puede el MgF2 tener la misma estructura que el CaF2 ¿Explique?
Solución:
Radios ionicos:
r(Mg2+
) = 0.66A
r(F-
) = 1.36A
r(Ca2+
)=0.99A
La relación de radios será: (MgF2)
( )
( ) 4853.0
36.1
66.0
Fr
Mgr 2
==−
+
La relación de radios será:
( )
( ) 728.0
36.1
99.0
Fr
Car 2
==−
+
Para el MgF2:
La relación de radios se encuentra en el intervalo 0.44 < 0.4853 < 0.732 por lo tanto NC
= 6.
Para el CaF2:
La relación de radios se encuentra en el intervalo 0.44<0.728<0.732 por lo tanto NC =
6.
Si tiene la misma estructura que la fluorita (CaF2)
5. El SrZrO3 tiene la estructura cristalina de la peroskita, determine la dirección
en la cual se tocan los iones y después calcular el parámetro de red y su densidad.
Solución:

5. Sr2+
O2+
zr4+
2rO
2-
rSr2+
a
a
rSr2+
a
rO2- rO2-
2r Hueco
rO2-
rO2-
a0
O2-
2r Zr4+
O2-
O2-
O2-
Calculo de la dirección en la cual se tocan los iones:
Supongamos que el ión de Zr4
no se encuentra presente y determinamos el tamaño del
hueco intersticial. En este caso los iones se tocaran a lo largo de una diagonal en la cara.
Diagonal = 22
aa +
Diagonal = 2a
( )
A66.3a
2
)A32.1A27.1(2
a
rOrSr22a 22
=
+
=
+= −+
Del hueco intersticial será:
2rhueco + 2rO-2
= a
rhueco =
( )
2
A32.1266.3 −
rhueco = 0.51A
Pero este tamaño del hueco es menor que del ión Zr4+
= 0.87ª. Este ión debe empujar a
los iones circundantes superpuestos con frecuencia cuando el ión Zr4+
esta acomodado;
los iones se tocan entre los de oxigeno y el zirconio.
Su parámetro de red será:
( ) ( )
A38.4a
A64.2A74.1a
A32.12A87.02a
rO2rZr2a
0
0
0
24
0
=
+=
+=
+= −+
Según la figura:
Nº iones Zr4+
= 1
Nº iones Sr2+
= 18*
8
1
=
Nº iones O2-
= 36*
2
1
=
Calcula de la masa SrZrO3

6. ( ) ( ) ( )
( ) ( ) ( )
g10x766.3m
10x023.6
163224.91162.871
m
N
.Oxig.A.PionesOºnZr.A.PionesZrºnSr.A.PionesSrºn
m
22
SrZrO
23SrZrO
242
SrZrO
3
3
3
−
−++
=
++
=
++
=
Calculo de la densidad SrZrO3
Sabemos que la
V
m
D =
( )
3
38
22
cm/g48.4
cm10x38.4
g10x766.3
=
=⇒
−
−
ρ
ρ
6. Supóngase que se añade 300 Kg de Na2O a 1000 Kg de SiO2 ¿Es capaz esta
combinación de formar un buen vidrio?
Solución:
Datos
P.M.(Na2O) = 23(2) +16 = 62g/mol
P.M.(SiO2) = 28 + 16(2) = 60g/mol
Calculamos el % en peso del Na2O y SiO2
%23ONa%
100*
1300
300
ONa%
2
2
=
=
%77SiO%
100*
1300
1000
SiO%
2
2
=
=
Calculamos la fracción molar del Na2O y SiO2
( )
( )
( ) ( )2
2
2
2
2
2
SiO.M.P
PesoSiO%
ONa.M.P
Peso%
ONa.M.P
ONaPeso%
OXNa
+
=
Reemplazando valores
224.0OXNa
60
77
62
23
62
23
OXNa
2
2
=
+
=

7. Sabemos que:
776.0XSiO
224.01XSiO
OXNa1XSiO1XSiOOXNa
2
2
2222
=
−=
−=⇒=+
Calculo de la relación O/Si
( )( ) ( )( )
( )( )
( )( ) ( )( )
( )( )
3.2
Si
O
776.01
776.02224.01
Si
O
XSiOSiOelenionesSiºN
XSiOSiOelenOionesºNOXNaONaelenionesºN
Si
O
22
4
22
-2
22
=
+
=
+
= +
Si es capaz de generar un buen vidrio debido a la relación O/Si < 2.5
7. Se tiene una cerámica sólida en KCl y FeO que contiene 15% O2, 30%Fe 25%K
y 30%Cl por peso.¿Cuantas vacantes de catión se presentaran en 500 celdas
unitarias de este material.
Solución:
El FeO tiene una estructura CCC (Tipo NaCl) con los iones Mg2+
en NC =6. El KCl
tiene una estructura CCC (tipo CsCl) con iones K+
en NC =o iones Cl-
en NC =8.
Nº iones Por celda 500 Celdas P.M. (g/mol)
En el FeO
4Fe2+
4(500) = 2000Fe2+
55.847
4O-2
4(500) = 2000º-2
16.00
En el KCl
1K+
1(500) = 500 K+
39.102
1Cl-
1(500) = 500 Cl-
35.453
Tomando como base: 100 g de cerámica sólida:
K = 25 Kg; O2 = 15 g; Fe = 30 g; Cl = 30 g
Calculo de la masa total de la cerámica sólida
( )
19
T
23T
22
T
10x00467.3m
g/uma10X023.6
uma453.35*50016*2000102.39*500847.55*2000
m
N
A.P*ClºNA.P*OºNA.P*KºNA.P*FeºN
m
−
−−++
=
+++
=
+++
=
Se sabe que para el FeO: Nº cationes Fe2+
+ Nº Vacancias = Nº de aniones O-2
..(1)
También:
( )( ) ( )
232
23
2
2
2
10x2354.3cationesFeºN
847.55
10x023.630
cationesFeºng30
N
A.PFeºN
mFe
=
=⇒==
+
+
+
+

8. ( )( ) ( )
232
23
2
2
2
10x6466.5anionesOºN
16
10x023.615
anionesOºng15
N
A.POºN
mO
=
=⇒==
−
−
−
−
Reemplazando estos valores en (1) se tiene
Nº de vacancias = 5.6466x1023
– 3.2354x1023
= 2.411x1023
Para el KClñ: Nº Cationes K+
+ vacancias = Nº aniones Cl……. (2)
También:
( )( ) ( )
23
23
10x851.3cationesKºN
102.39
10x023.625
cationesKºng25
N
A.PKºN
mK
=
=⇒==
+
+
+
+
( )( ) ( )
23
23
10x0966.5anionesClºN
453.35
10x023.630
anionesClºng30
N
A.PClºN
mCl
=
=⇒==
−
−
−
−
Reemplazando estos valores en (2) se tiene:
Nº vacancias = 5.0966x1023
– 3.851x1023
= 1.246x1023
Vacancias de catión totales en 100 g = 2.411x1023
+ 1.246x1023
= 3.567x1023
Calculo del Nº de vacancias en 500 celdas unitarias.
( )( )
( )( )
cationicasVacancias1100
g100
10x657.3g10x00467.3
100
100genVacanciasºNm
2319
T
=
=
=
−
8. 1000 Kg de arcilla caolinita Al2(Si2O5)(OH)4 se calienta para retirar el hidrogeno
en forma de agua a)Cuantos Kg se pierde en peso. b) Cuales serán las
temperaturas del liquidus y del solidus de la mezcla resultante de Al2O3 y SiO2
a) Al calentar se retira el agua según la siguiente reacción:
Al2(Si2O5)(OH)4 ⇒ Al2O3 + 2SiO2 + 2H2O

9. Peso molecular del Al2(Si2O5)(OH)4 = 258.15 g/g-mol
Peso molecular del H2O: 18 g/g-mol
El % en pérdida de peso será:
( )
139.6Kg1000*%96.13seríaPeso96.13OH%
molg/g15.258
molg/g18*2
OH%
100*
OH)OSi(Al.PM
OH.PM2
OH%
2
2
4522
2
2
=⇒=
−
−
=
=
% de Al2O3 en la arcilla
( )
395Kg1000*%50.39seríaPeso50.39OAl%
molg/g15.258
molg/g96.101
OAl%
100*
OH)OSi(Al.PM
OAl.PM
OAl%
32
32
4522
32
32
==⇒=
−
−
=
=
% de SiO2 en la arcilla
( )
465.5Kg1000*%55.46seríaPeso55.46SiO%
molg/g15.258
molg/g09.60*2
SiO%
100*
OH)OSi(Al.PM
SiO.PM2
SiO%
2
2
4522
2
2
==⇒=
−
−
=
=
b) Tomando como base los 1000 Kg de arcilla habra: 395 Kg de Al2O3 y 465.5 Kg de
SiO2 por consiguiente la composición de la arcilla después de evaporar el agua será:
% Al2O3 en peso:
%62.45OAl%
100*
856
OKgAl395
OAl%
100*
OHelevaporardedespuésorefractarideltotalPeso
OKgAl
OAl%
32
32
32
2
32
32
=
=
=

10. ( )
( )
( )
Kg32.29OAl
80*
22.278
96.101
OAl
80*
SiO.OAl.PM
OAl.PM
OAl
32
32
232
32
32
=
=
=
( )
( )
( )
Kg28.45OAl
160*
32.360
96.101
OAl
160*
OH.SiO4.OAl.PM
OAl.PM
OAl
32
32
2232
32
32
=
=
=
% SiO2 en peso:
54.38%SiO%
856
KgSiO5.465
SiO%
100*
OHelevaporardedespuésorefractarideltotalPeso
SiO.Kg
SiO%
2
2
2
2
2
2
=
=
=
Según el diagrama SiO2 – Al2O3 esta ceámica se representa en la linea discontinua.
La temperatura del liquidus: 1830 ºC
La temperatura del solidus: 1597 ºC
9. Se produce una arcilla: en 80 Kg de anortita (CaO.Al2O3.2H2O), 160 Kg de
montmorilonita (Al2O3.4SiO2.H2O) y 80 Kg de caolinita (Al2O3.2SiO2.2H2O). La
arcilla es secada y después horneada a 1500ºC. Cual será la composición y
temperaturas del liquidus del producto final.
Solución:
1. Determinar la composición final de la cerámica después del horneado:
Calculo de los pesos moleculares de los óxidos:
Peso molecular SiO2 = 28.09 + 2(16) = 60.09 g/g-mol
Peso molecular CaO = 40.08 + 16 = 56.08 gg-mol
Peso molecular Al2O3 = 2(27.0) + 3(16) = 101.96 gg-mol
Peso molecular H2O = 2(1) + 16 = 18 gg-mol
En 80 Kg de CaO.Al2O3 .2SiO2 el peso de cada oxido es:
( )
( )
( )
Kg56.34SiO
80*
22.278
09.602
SiO
80*
SiO.OAl.PM
SiO.PM2
SiO
2
2
232
2
2
=
=
=
( )
( )
( )
Kg12.16CaO
80*
22.278
08.56
CaO
80*
SiO.OAl.PM
CaO.PM
CaO
232
=
=
=
En 160 Kg de Al2O3.4SiO2.H2O el peso de cada oxido es:

11. ( )
( )
( )
Kg60.31OAl
80*
14.258
96.101
OAl
80*
OH2.SiO2.OAl.PM
OAl.PM
OAl
32
32
2232
32
32
=
=
=
( )
( )
%36.5CaO
100*
84.300
12.16
CaO
=
=
( )
( )
( )
Kg73.106SiO
160*
32.360
09.604
SiO
160*
OH.SiO4.OAl.PM
SiO.PM4
SiO
2
2
2232
2
2
=
=
=
( )
( )
( )
Kg0.8OH
160*
32.360
18
OH
160*
OH.SiO4.OAl.PM
OH.PM
OH
2
2
2232
2
2
=
=
=
En 80 Kg de Al2O3.2SiO2.2H2O el peso de cada oxido es:
( )
( )
( )
Kg24.37SiO
80*
14.258
09.602
SiO
80*
OH2.SiO2.OAl.PM
SiO.PM2
SiO
2
2
2232
2
2
=
=
=
( )
( )
( )
Kg16.11OH
80*
14.258
182
OH
80*
OH2.SiO2.OAl.PM
OH.PM2
OH
2
2
2232
2
2
=
=
=
Después del secado y horneado, el agua ha sido retirado de modo que el peso final total
de la cerámica es:
Peso total = 80 + 160 + 80 – (8+11.16) =300.84 Kg
La composición de la cerámica después de horneada ósea cocida es:
( )
( )
%30.35OAl
100*
84.300
60.3128.4532.29
OAl
32
32
=
++
=
( )
( )
%34.59SiO
100*
84.300
24.3773.10656.34
SiO
2
2
=
++
=

12. Según el grafico aleación ternaria CaO – SiO2 –Al2O3 la temperatura del liquidus
aproximada es:
10. Una muestra cúbica policristalina de ZrO2 completamente establecida tiene
una tenacidad a la fractura de KIC = 4.0 MPa m . Cuando es producida en un
ensayo de flexión de cuatro puntos.
Prueba de tenacidad a la fractura mediante un ensayo de flexión de 4 puntos.
a) Si la muestra rompe a un esfuezo de 500MPa ¿Cuál es el tamaño de la
mayor grieta superficial posible (suponer Y = 1).
b) La misma prueba se hace con una muestra de ZrO2 parcialmente
establecida este material es endurecido por transformación y tiene un KIC =
14.0MPa m . Si ese material tiene la misma distribución de las grietas que
la muestra totalmente estabilizada ¿Qué tensión debe aplicarse para
producir la fractura.
Solución:
a) como KIC = yC.f πσ
Prueba de tenacidad a la fractura mediante un ensayo de 4 puntos.
Aquí:
mMPa0.4K
1Y
MPa500f
IC =
=
=σ
Despejando la longitud de grieta superficial (C) se tiene:
( )
( ) ( )
m37.20m10x037.2C
MPa5001
mMPa0.4
C
fY
K
C
5
22
2
22
2
IC
µ
π
σπ
==
=
=
−
Como la grieta es superficial la longitud de la grieta es igual a C.
b) Cuando el material es parcialmente estabuilizado KIC aumenta entonces se
tiene:

13. Material de MgO
L=44.5 mm
P=5560N
R
?f
1Y
10x037.2C
mMPa0.14K
5
IC
=
=
=
=
−
σ
Y.C.fK IC πσ=
MPa1750f
)1(*m10x037.2*
mMPa0.14
f
Y.C.
K
f
5
IC
=
=
=
−
σ
π
σ
π
σ
11. Un material circular de MgO es cargada en flexion por tres puntos. Calcule el
radio mínimo posible de la probeta sin que la probeta se rompa cuando se aplica
una carga de 5560N. Si se sabe que el modulo de rotura es 310MPa y la separación
entre los puntos de apoyo es 44.5 mm.
Solución:
Datos:
P = 5560 N
( ) MPa310roturadeulomodmr =σ
L = 44.5 mm = 44.5x10-3
m
R =¿?
Para una sección circular se cumple:
mm873.0m10x73.8R
106x310*1416.3
310x5.44*5560*3
R
PL3
Rdonde
R
PL3
rm
4
3/1
3/1
mr
3
==





 −
=






==
−
πσπ
σ
12. El material refractario fabricado de un material de SiO2 – 45%Al2O3 se usará
para contener acero fundido a 1600ºC (a) que porcentaje del refractario se fundira
en estas condiciones, b) es esta una buena elección de un material refractario?
Solución:

14. C
W
a) Según el diagrama de equilibrio SiO2 – Al2O3 el tipo de refractario es chamota. Se
nota que a 1600ºC para este refractario existe líquido y mullita. Aplicando la regla de la
palanca a 1600ºC se tiene:
Porcentaje de líquido a 1600ºC
%9.40Líquido
100*
672
4572
Líquido
=
−
−
=
Entonces: En esta condición el porcentaje de refractario que se funde será 40.9%
b) Para este tipo de material refractario se acepta un porcentaje máximo de líquido en el
refractario de 20%. Por lo tanto no es una buena elección para contener acero fundido a
1600ºC.
13. Una muestra policristalina de ZrO2 completamente establecida tiene una
tenacidad a la fractura de KIC = 3.8 MPa m . Obtenida mediante ensayo de
flexión a cuatro puntos.
a) Si la muestra rompe a una tensión de 450MPa ¿Cuál es el tamaño de la
mayor fisura superficial posible (suponer Y = π ).
b) La misma prueba se hace con una muestra de ZrO2 parcialmente
establecida. Este material cerámico tenaz tiene 12.5 MPa m . Si este
material tiene la misma distribución de las fisuras para la muestra
totalmente estabilizada ¿Qué tensión debe aplicarse para producir la
fisura?
Solución:
a) como KIC = yC.f πσ
Prueba de tenacidad a la fisura mediante ensayo de flexión de 4 puntos:
Aquí:
mMPa8.3K
Y
MPa450f
IC =
=
=
π
σ
Despejando la longitud de grieta superficial (C) se tiene:
( )
( ) ( )
m23.7m10x23.7C
MPa450
mMPa8.3
C
fY
K
C
6
22
2
22
2
IC
µ
ππ
σπ
==
=
=
−
Como la grieta es superficial la longitud de la grieta es igual a C.

15. b) Cuando el material es parcialmente estabuilizado KIC aumenta entonces se tiene:
?f
1Y
10x037.2C
mMPa0.14K
5
IC
=
=
=
=
−
σ
Y.C.fK IC πσ=
MPa1750f
)1(*m10x037.2*
mMPa0.14
f
Y.C.
K
f
5
IC
=
=
=
−
σ
π
σ
π
σ
UNIVERSIDAD NACIONAL DE
TRUJILLO
FACULTAD DE INGENIERIA
ESCUELA DE INGENIERIA
METALURGICA
Curso: Cerámica y Refractarios
Tema:
Laboratorio Nº 1

16. Docente:
Ing. Purizaga Fernández Ismael
Semestre:
2006-I
Alumnos:
Neira Anticona Jesus
Muñoz Sánchez Erasmo
Salinas Horma Michel
Solís Rodas Charlie
Roña Zarate Raymi
Vásquez Vásquez Michel
Trujillo-Perú
2006