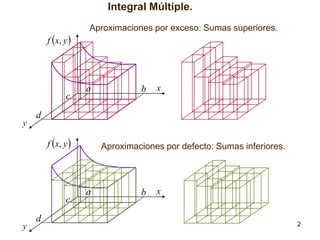
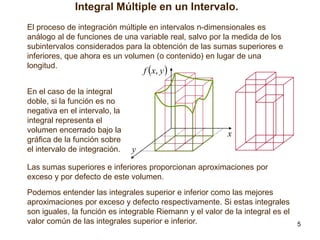
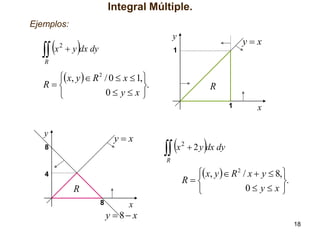
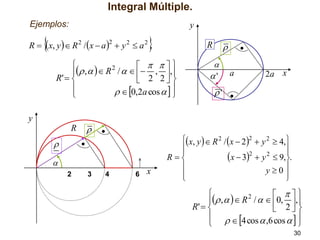
El documento presenta conceptos sobre la integral múltiple, incluyendo su definición en intervalos n-dimensionales, aproximaciones mediante sumas superiores e inferiores, y condiciones para que una función sea integrable. También introduce la integración en recintos más generales y el teorema de Fubini para calcular integrales múltiples mediante integración reiterada.

1. Integral Múltiple.
f x, y 
y
integral doble
c
y
a
d
b x
c
d
a
b
x
Conceptos previos: intervalo n-dimensional, partición, sumas
superiores e inferiores, integral de Riemann.
Integral múltiple mediante integración reiterada: Teorema de Fubini.
f x, y 
integral
doble
y
x
Integración en recintos más
generales: medida-Jordan de un
conjunto.
1

2. Integral Múltiple.
f x, y 
c
y
Aproximaciones por exceso: Sumas superiores.
a
x
d
f x, y 
c
y
b
d
Aproximaciones por defecto: Sumas inferiores.
a
b
x
2

3. Integral Múltiple en un Intervalo.
Definición: Un intervalo n-dimensional (o recinto rectangular) es
n
un conjunto
I  a1 , b1  a2 , b2  ... an , bn    ai , bi   R n .
i 1
z
y
Ejemplos:
1,3 2,3
0,2 0,2 1,2
3
2
2
(ortoedro)
1
1
(rectángulo)
1
0
x
 I1   3  13  2  2.
1
2
3
2
x
1
y
2
 I 2   2  02  02  1  4.
Definición: La medida de un intervalo n-dimensional es
n
 I   b1  a1  b2  a2  ... bn  an   bi  ai  R  .
i 1
En el caso de intervalos de R 2 se trata de un área, y de un volumen
3
para intervalos de R .
3

4. Integral Múltiple en un Intervalo.
Definición: Una partición P de un intervalo n-dimensional está
formada por n particiones P , P2 ,...,Pn de a1 , b1 , a2 , b2 ,...,an , bn 
1
respectivamente.
P  P , P ,...,P .
1
2
n
Así, una partición divide un intervalo n-dimensional en subintervalos
cerrados que se solapan en las fronteras.
y
Particiónes de 1,3 2,3,
z
y
3
3
2
Ejemplos:
2
1,3 2,3
1
0,2 0,2 1,2
1
2
3
1,3 2,3
1
x
1
2
3
x
2
2
x
y
2
Partición de 0,2 0,2 1,2.
4

5. Integral Múltiple en un Intervalo.
El proceso de integración múltiple en intervalos n-dimensionales es
análogo al de funciones de una variable real, salvo por la medida de los
subintervalos considerados para la obtención de las sumas superiores e
inferiores, que ahora es un volumen (o contenido) en lugar de una
longitud.
f x, y 
En el caso de la integral
doble, si la función es no
negativa en el intervalo, la
integral representa el
volumen encerrado bajo la
gráfica de la función sobre
el intervalo de integración.
x
y
Las sumas superiores e inferiores proporcionan aproximaciones por
exceso y por defecto de este volumen.
Podemos entender las integrales superior e inferior como las mejores
aproximaciones por exceso y defecto respectivamente. Si estas integrales
son iguales, la función es integrable Riemann y el valor de la integral es el
valor común de las integrales superior e inferior.
5

6. Integral Múltiple en un Intervalo.
Definición: Sea f : I  R n  R definida y acotada en el intervalo
n-dimensional I . Dada una partición P  P , P2 ,...,Pn  de I
1
con k subintervalos, en cada subintervalo I i
M i  sup f x ,
xI i
mi  inf f x .
xI i
Llamamos suma superior e inferior respectivamente de f para
la partición P a
k
S  f , P 
s f , P  
M
i
  I k ,
i 1
k
 m   I
i
k
.
i 1
Proposición: Para cualquier partición P de I se cumple que
S  f , P   s f , P .
6

7. Integral Múltiple en un Intervalo.
Definición: Decimos que una partición P  P , P2 ,...,Pn  es más fina
1
que otra Q  Q1 , Q2 ,...,Qn  , esto es, P  Q , si
P  Q1 , P2  Q2 , ...,Pn  Qn .
1
Proposición: Si P es más fina que Q , entonces
S  f , P  S  f , Q,
s f , P  s f , Q.
Así, cualquier sucesión particiones sucesivamente más finas de un
intervalo genera una sucesión de sumas superiores decreciente, y una
partición de sumas superiores creciente.
Proposición: Para cualesquiera particiones P y Q de I se
cumple que
S  f , P  s f , Q.
Por tanto, las sumas superiores están acotadas inferiormente por cualquiera
de las sumas inferiores, y las sumas inferiores están acotadas
superiormente por cualquiera de las sumas superiores.
7

8. Integral Múltiple en un Intervalo.
Definición: Llamamos integral superior de la función f en el
intervalo I al ínfimo de sus sumas superiores.
P más finas
  ... f x , x ,..., x dx dx ...dx
s
2
n
1
2
n
 inf S  f , P .
P
I
Análogamente, la integral inferior es
  ... f x , x ,..., x dx dx ...dx
1
P más finas
S
1
2
n
1
I
2
n
 sup s f , P .
P
Estas integrales existen y tienen valores reales siempre que la
función es acotada, y se cumple que
  ... f x , x ,..., x dx dx ...dx
1
I
2
n
1
2
n
   ... f x1 , x2 ,..., xn dx1dx2 ...dxn .
I
8

9. Integral Múltiple en un Intervalo.
Definición: Sea f : I  R n  R definida y acotada en el intervalo
n-dimensional I . Decimos que f es integrable en I si y sólo si
  ... f x , x ,..., x dx dx ...dx
1
2
n
1
2
   ... f x1 , x2 ,..., xn dx1dx2 ...dxn .
n
I
I
En ese caso, la integral de f en I ,
  ... f x , x ,..., x dx dx ...dx ,
1
2
n
1
2
n
I
es el valor común de las integrales superior e inferior.
9

10. Integral Múltiple en recintos más generales.
f x, y 
Es posible definir integrales
múltiples en conjuntos o recintos
que no son intervalos, siempre
que estos sean medibles-Jordan.
Se construyen por extensión de
la función por cero a un intervalo
que contenga el recinto de
integración R e integrando la
nueva función en el intervalo.
 f x  x  R,
g x   
x  R.
 0
Así, la función f es integrable
en R si g es integrable en I ,
y en ese caso ambas integrales
tienen el mismo valor.
x
R
y
y
g x   0
I
R
g x   f x 
x
10

11. Integral Múltiple en recintos más generales.
Definición: (Contenido interior y exterior de Jordan) Sea R un subconjunto
de un intervalo I . Para toda partición P de I , definimos J R, P  como la
suma de los contenidos de todos los subintervalos que contienen sólo puntos
interiores de R , y J R, P  como la suma de los contenidos de los
subintervalos que contienen puntos del interior o la frontera de R .
y
Los contenidos interior y exterior de
Jordan de R son, respectivamente,
cR   sup J R, P , c R   inf J R, P .
P
P
Un conjunto R es medible-Jordan si
cR   c R ,
x
en cuyo caso este valor común es el contenido de Jordan, cR  , de R .
En esencia, un conjunto es medible-Jordan si se puede calcular su
contenido mediante un proceso de integración de Riemann (de su función
característica).
Proposición: Un conjunto es medible-Jordan si y sólo si su frontera tiene
medida nula. Para ello es condicion suficiente que su frontera sea una
2
3
linea si R  R ,o una superficie bidimensional si R  R .
11

12. Integral Múltiple: Condiciones de Integrabilidad.
Proposición: (CNS) Sea f : I  R n  R definida y acotada en el
intervalo n-dimensional I . Entonces f es integrable en I si y
sólo si para todo   0 existe una partición P de I tal que
S  f , P   s f , P    .
Proposición: (CS) Si f : I  R n  R es continua en el intervalo ndimensional I , entonces es integrable en I .
Proposición: Sea f : I  R n  R continua en el recinto R  I .
Entonces f es integrable en R si y sólo R es medible-Jordan.
Proposición: Sea f : I  R n  R definida y acotada en un recinto
medible-Jordan R  I . Si f tiene un número finito de puntos
de discontinuidad en R , entonces f es integrable en R .
12

13. Integral Múltiple: Propiedades.
Las propiedades de la integral múltiple son análogas a las de la
integral de funciones de una variable real; linealidad, monotonía,
aditividad respecto al intervalo. Esta última es la única que requiere
un nuevo matiz relevante.
Proposición: Sea f : I  R n  R definida y acotada en un
recinto R  I . Y sean R1 y R2 dos subconjuntos de R tales que
R1  R2  R,
Int R1   Int R1   o.

Entonces f es integrable en R si y sólo si lo es en R1 y en R2 y
se cumple que
y
 ... f x , x ,...,x dx dx ...dx
  ... f x , x ,...,x dx dx ...dx
  ... f x , x ,...,x dx dx ...dx .
1
2
n
1
2
n
R2
R
1
2
n
1
2
n
R1
1
R2
2
n
1
2
n
R1
x
13

14. Integral Múltiple: Integración reiterada.
El siguiente resultado proporciona un procedimiento para calcular
la integral múltiple de una función continua en un intervalo ndimensional mediante un cálculo reiterado de integrales de
funciones de variable real.
Proposición: (Teorema de Fubini) Sea f : I  R n  R continua
n
en el intervalo I  a , b  a , b  ... a , b    a , b   R n .
1 1
2 2
n n
i i
i 1
Se verifica que
 ... f x , x ,...,x dx dx ...dx


    ...  f x , x ,...,x dx



1
I
2
n
1
b1
b2
a2
an
n
bn
a1
2
1
2
n


n ... dx2  dx1 ,



dónde cada integral se resuelve tratando al resto de variables
como constantes. El resultado es independiente del orden de
integración.
14

15. Integral Múltiple: Integración reiterada.
En el caso de integrales dobles,
f x, y 
I  a, b c, d   R 2 .

f x, y 0
c
y
d
y

a
b

x
F x, y 
 f x, y .
x
0
f x, y  dx dy 
I
f x, y dx dy 
b d

a c
d b
 
c


a

f x, y dx  dy 


d
c
F x, y b dy
a
 F b, y   F a, y  dy   F b, y  dy   F a, y  dy.
4
d
d
c

y
d
c
c
Ejemplo:
2
I  1,5 2,4
1
5
x
  x
5
1
4
2
2

 y dx dy
15

16. Integral Múltiple: Integración reiterada.
Este método de integración reiterada se puede extender para
conjuntos mas generales. Pero en este caso los extremos de
integración no son, en general, fijos, y el orden de integración es
relevante para que el cálculo sea más o menos laborioso.
Ejemplo 1:
y
g 2 x 
R
a

R

g1 x 
b
x, y   R 2 / a  x  b,


R
.
 g1 x   y  g 2 x  



f x, y dx dy 
R
b g 2  x 

f x, y dy  dx.

a  g1  x 

 
Gx, y 
 f x, y .
y
x
b g 2  x 

f x, y dx dy  
f x, y dy  dx 
a  g1  x 

 

x
Gx, y g 2x  dx
g
b
a
1
 Gx, g x  Gx, g x dx   Gx, g x dx   Gx, g x dx.
b
a
b
2
1
a
b
2
a
1
16

17. Integral Múltiple: Integración reiterada.


R  x, y   R / g1  y   x  g 2  y  .

g2 y
y
Ejemplo 2:
2
f x, y dx dy 
R
d
g1  y 
R
d  g2  y 

f x, y dx  dy.
g1  y 

 
c


c
x
En ocasiones es necesario dividir el recinto en varios subrecintos.

g 3 x 
y

R  x, y   R 2 / g1  y   y  g 2  y , y  g3  y  .
y
3  y   2  y 
g 2 x 
e
Ejemplo 3:
g1 x 
R2
R1
d
R2
1  y 
R1
c
a
b
c
x
x
17

18. Integral Múltiple.
Ejemplos:
 x
2
y
 y dx dy
yx
1
R
x, y   R 2 / 0  x  1,
R
.
0 y x 

R
1
y
yx
8
 x
2
x

 2 y dx dy
R
x, y   R 2 / x  y  8,
R
.
0 y x 

4
R
8
x
y  8 x
18

19. Integral Múltiple.
Ejemplos:

R
y
1
xy dx dy
x, y   R 2 / y  x 2 ,


R
0  x  y  1,.

0 x 


y
1
x
y  1 x
R
R
4
-2
R
 3 y dx dy
4
2
y  x2
x  4  y2
x
x, y   R 2 / x  4  y 2 ,


R
0  x  4,.

0 y4 


19

20. Integral Múltiple.
Ejemplos:

R
y
xy 3 dx dy
y  x2
1
x, y   R 2 / 0  y  x 2 ,
R
.
0  x 1 

y
yx
yx
2
R
1

x
y 2 sen x dx dy
R
x, y   R 2 / y  x 2 ,
R
.
yx 

1
R
1
x
20

21. Integral Múltiple.
Ejemplos:

R
y
yx
8
xy dx dy
x, y   R 2 / 2  x  6,


R
0  y  x,.

x y 8 


y
2
R1 R2
2
4
6
8
x
y  8 x
 xy dx dy
2
R
R
-3
R1 '
R2 '
4
3
x
2


y2
2 x
 1,
x, y   R / 
R
9
4
.

x, y  0 


-2
21

22. Integral Múltiple: Cambio de Variable
En algunos casos es útil hacer un cambio de variable para calcular el valor
de una integral múltiple. Esto puede deberse a ello facilite la obtención de
una primitiva para la función subintegral, o bien a que transforme el recinto
de integración en otro –referido a las nuevas variables- para el cual el
proceso de integración reiterada sea más sencillo.
y
v
R
x, y   g u, v
x
R'
u
Las principales diferencias respecto al cambio de variable en integrales
de funciones de variable real son que en las integrales múltiples la
función g para el cambio de variable debe ser una función vectorial
biyectiva (aunque este requisito se puede suavizar), y el papel que en las
integrales de variable real tenía la derivada de la transformación lo
desempeña ahora el determinante jacobiano de g .
22

23. Integral Múltiple: Cambio de Variable
 ... f x dx dx ...dx
1
2
x  g u ,
n
x1  g1 u1 , u 2 ,...,u n ,
R
g R'  R
x2  g 2 u1 , u 2 ,...,u n ,
R
g u   x
R'
g  g1 , g 2 ,...,g n .
x
u
...
xn  g n u1 , u 2 ,...,u n .
I
Sea f : I  R n  R una función continua en un conjunto compacto y
medible-Jordan R  I .
Y sea g : D  R n  R n una función vectorial g  g1 , g 2 ,...,g n 
biyectiva que transforma el conjunto R' en R .
Si g es de clase C 1 y su determinante jacobiano es no nulo en un
abierto que contenga a R' , entonces se cumple que
 ... f x dx dx ... dx   ... f g u  Jg u  du du ... du ,
1
R
 
donde Jg u
2
1
n
2
n
R'
es el valor absoluto del determinante jacobiano de g .
23

24. Integral Múltiple: Cambio de Variable
Cambio a coordenadas polares: Suele
aplicarse en integrales dobles cuyo recinto de
sección
integración es un círculo, sección circular, corona circular
o sección de corona circular, ya que en estos
casos el recinto expresado en términos de las
coordenadas polares es un recinto rectangular. sección
de corona
circular

y
corona
circular
R'
R

x
Ecuaciones de cambio a coordenadas polares:
x  g1  ,     cos  ,
y  g 2  ,     sen  .
Jacobiano de la transformación:
Jg  ,    .
y
x, y 


x
24

25. Integral Múltiple.
Ejemplos:

R
y
sección
circular
3
x 2 dx dy
x, y   R 2 / x 2  y 2  9,
R
.
x, y  0 


2
-3
R
3
x
-3
yx
y
3
R
-3

4
x
y
3

6
x
3
sección
circular
-3
 xy dx dy
R


x, y   R 2 / x 2  y 2  9,




R
x  y,.

x 


y

3 


25

26. Integral Múltiple.
Ejemplos:
 x
R
2
y
yx
3
dx dy
x, y   R 2 / x 2  y 2  9,
R
.
x y0 

-3
3
R
x
-3
y
yx
5
R
-5
 y dx dy
R
5
x
x, y   R 2 / x 2  y 2  25,
R
.
x y 

-5
26

27. Integral Múltiple.
Ejemplos:
y

corona
circular
xy dx dy
R
R
x, y   R / x  y  9,


R
.
2
2

x y 4


2
2
2
yx
y
1
sección
de corona
circular
x
R
x
3
3
 y dx dy

4
R
2
x, y   R 2 / x 2  y 2  9,


2
2
R
x  y  1,.

x y0 


27

28. Integral Múltiple.
Cuando la circunferencia que determina el recinto no está centrada en el
origen suele ser útil hacer un cambio de variable previo al cambio a
coordenadas polares.


R  x, y   R 2 / x  a 2   y  b2  r 2 .
u  x  a,
v  y  b.

J1  1.

R'  u, v   R 2 / u 2  v 2  r 2 .
u   cos  ,
v   sen  .
v
y
R
b
J 2  .
 ,    R 2 /   0,2 ,


R' '  
.

  0, r  


u
r
a
x
28

29. Integral Múltiple.
Sin embargo, en algunos casos es posible resolver el problema con un
único cambio a coordenadas polares que, en general, no producirá un
recinto rectangular.
y
Ejemplo:


R
x 2  y 2 dx dy

R
 x, y   R /  x  2   y  4, 


R
.
y0 



2
2
2
2


 ,    R 2 /   0,  ,

 2
R'  



  0,4 cos   


h
4
x


h
h

  h cos 
29

30. Integral Múltiple.
Ejemplos:
y


R  x, y   R 2 / x  a 2  y 2  a 2 .


 ,    R 2 /      ,   , 

 2 2
R'  



  0,2a cos   


y
R



2
3
4
6
x

R

'
a
2a x
'
x, y   R 2 / x  22  y 2  4,



2
2
x  3  y  9,.
R


y0 






 ,    R 2 /   0,  ,

 2
R'  


   4 cos  ,6 cos   


30

31. Integral Múltiple.
y
Ejemplos:
6
x, y   R 2 / x 2   y  32  9,


R
.

x0 




 ,    R 2 /   0,  ,

 2 .
R'  



  0,6sen  




R
3

h

x
h
  h sen 
y

2b

b
'


h




R  x, y   R 2 / x 2   y  b2  b 2 .
R
' 
x
 '  2bsen  2bsen '.
 ,    R 2 /   0,  ,


R'  
.

  0,2bsen  


31