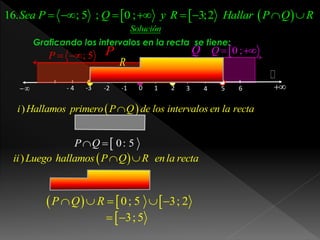
El documento presenta una serie de ejercicios sobre operaciones con intervalos en una recta numérica. Se grafican los intervalos dados y se calculan sus uniones, intersecciones y diferencias según sea el caso. Se resuelven 12 ejercicios individuales y 5 ejercicios combinados que involucran 3 intervalos.

2. 50-1-2 3
2
 4321
AB
30-1 1-3 2-2
En el grafico la parte sombreada es la uni n de los dos intervalosó
 1. 1;3 3;1Sea A y B Hallar A B    
Solución
3; 3A B    
32. ; 0;5
2
Sea P y Q Hallar P Q     
Solución
Graficando los intervalos en la recta se tiene
P Q3 ;
2
P    0;5Q  
La unión de los dos intervalos es la parte sombreada que vemos
3 ;
2
P Q    
Haciendo la gráfica de los intervalos se tiene
3;1B  
1 ;3A 

3. 3. ;1 1;2Sea C y D Hallar C D      
Solución
0-4 -3 21-1-2
Haciendo la gráfica de los intervalos se tiene
La unión de los dos intervalos es la parte sombreada que vemos
 4. 4;3 4; 8 ,Sea P y Q hallar P Q   
Solución
Haciendo la grafica de los intervalos en la recta se tiene
;1C   1; 2D  
;2C D   
0-4 -3 21-1-2 3 4 5 6 87
 4; 3P  P 4 ;8Q  Q
Luego la unión de los dos intervalos es la parte sombreada que vemos
 4;3 4 ;8P Q    
DC

4.  5. 3; 4 1; 7Sea A y B Hallar A B    
Solución
Graficando los intervalos en la recta se tiene:
0-4 -3 21-1-2 3 4 5 6 7
 3; 4A  
1; 7B   B
A
Luego la intersección de los dos intervalos es la parte que se sombrea
1;4A B   
6. 2; 0 ; 6Sea P y Q Hallar P Q    
Solución
Graficando los intervalos en la recta se tiene:
0-3 21-1-2 3 4 5 6 7
 2;P    P0 ; 6Q  Q
Luego la intersección de los dos intervalos es la parte que se sombrea, ya
que esta dentro del otro intervalo 0 6P Q   

5. 7. 5;0 2 ; 7Sea R y S Hallar R S   
Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7
5;0R   2 ;7S 
Observando los intervalos en la recta, no tienen elementos iguales o no
hay intersección entre ellos. R S   
R S
5
8. 3; ;
2
Sea T y U Hallar T U     
Solución
Graficando los intervalos en la recta se tiene:
30-1 1-3
2-2 45
2
U
T3 ;T   
5
;
2
U   
Luego la intersección de los dos intervalos es la parte que se sombrea
5
3 ;
2
U T   

6. 9. 2; 3 0 ; 5Sea A y B Hallar A B   
Solución
Graficando los intervalos en la recta se tiene:
30-1 1-3 2-2 43 5
A B 2; 3A   0 ; 5B 
Luego la diferencia de los dos intervalos es la parte que se sombrea, ya que
dice A-B ,además ,pero a “A” sí, de allí que es cerrado en la respuesta0 B
 2;0A B   
110. ; 4 ;
2
Sea C y D Hallar D C     
Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 41
2

1;
2
C   4 ;D   
C
D
Luego la diferencia de los dos intervalos es la parte que se sombrea, yaque
dice D-C con cerrado.1
2
1 ;
2
D C    


7. 11. ;1 3 ;9Sea E y F Hallar F E   
Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7 8 9
;1E   3 ;9F E F
En este caso, la diferencia es el mismo “ F” ya que dice F – E
3 ;9F E  
12. 2; 5 ;8Sea G y H Hallar G H    
Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7 8 9
G
H; 8H  
2 ; 5G  
En este caso no hay diferencia ,ya que “G” está dentro de “H” y todos los
elementos iguales de “G” se han eliminado
G H   

8. Ejercicios combinados de 3 intervalos
   13. ; 1 ; 4 ;4 2;6Sea A B y C Hallar A C B       
Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7 8 9
; 1A   
 4 ;4B  
2;6C A
B
C
)i Hallamos primero A C en la recta
 )ii Luegohallamos A C B seobserva enla recta 
; 1 2 ; 6A C     
  4; 1 2; 4A C B     
Recuerda que
la intersección
es, los
elementos
comunes de
 A C B 

9. Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7 8- 6 1
2
   14. ; 1 ; 4 ;4 2;6Sea A B y C Hallar B A C       
; 1A   
 4 ;4B  
2;6C A
B
C
)i Hallamos primero A C en la recta
; 1 2; 6A C    
 )ii Luego hallamos B A C se observa enla recta 
  1;2B A C    
Recuerda que
los elementos
comunes se
eliminan y se
toma todo lo
que queda en
B

10. Solución
Graficando los intervalos en la recta se tiene:
- 4- 5 0-3 21-1-2 3 4 5 6 7 8- 6 1
2
   15. ; 1 ; 4 ;4 2;6Sea A B y C Hallar A C B       
; 1A   
 4 ;4B   2;6C A
B
C
)i Hallamos primero A C en la recta
; 1 2; 6A C    
 )ii Luego hallamos A C B se observa enla recta 
  ; 4 4; 6A C B       
Recuerda que
los elementos
comunes se
eliminan y se
toma todo lo
que queda en
AUC

11.    16. ; 5 ; 0 ; 3;2Sea P Q y R Hallar P Q R       
Solución
- 4 0-3 21-1-2 3 4 5 6 
Graficando los intervalos en la recta se tiene:
; 5P   0 ;Q  
 3;2R  
P Q
R
 )i Hallamos primero P Q de los intervalos en la recta
 0: 5P Q 
 )ii Luego hallamos P Q R enla recta 
   

0; 5 3; 2
3; 5
P Q R    
 

12.    17. ; 5 ; 0 ; 3;2Sea P Q y R Hallar P Q R       
- 4 0-3 21-1-2 3 4 5 6 
; 5P   0 ;Q  
 3;2R  
P Q
R
Solución
Graficando los intervalos en la recta se tiene:
 )i Hallamos primero P Q de los intervalos en la recta
  ;P Q    
 )ii Luego hallamos P Q R enla recta 
  ; 3 2;P Q R      

13.     18. ; 2 ; 2 ; 4; 4Sea A B y C Hallar A B C        
Solución
Graficando los intervalos en la recta se tiene:
- 4 0-3 21-1-2 3 4 5 6 
; 2A  
 2 ;B   
 4; 4C  
C
A B
 )i Hallamos primero A B de los intervalos en la recta
  2 2A B   
 )ii Luego hallamos A B C enla recta 
   4 4A B C    