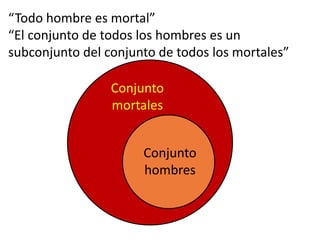
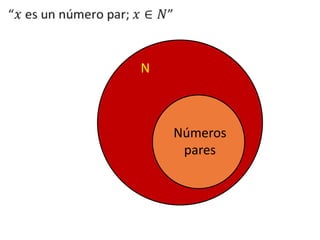
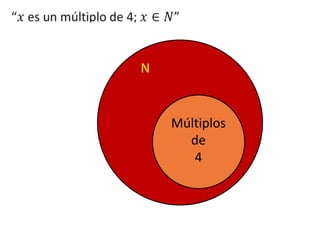
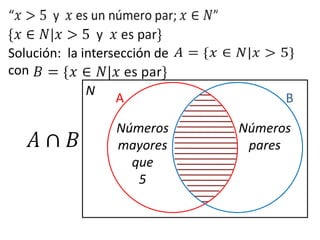
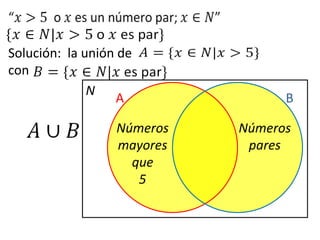
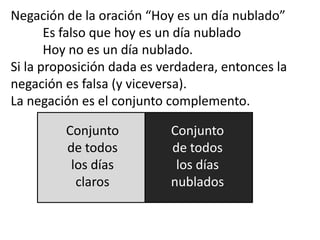
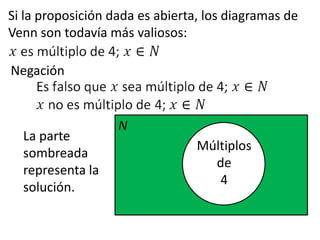
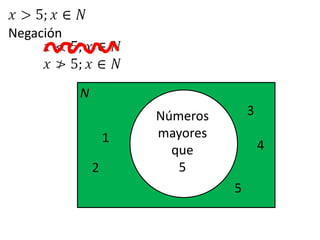
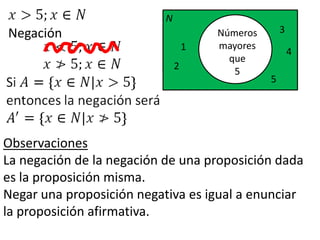
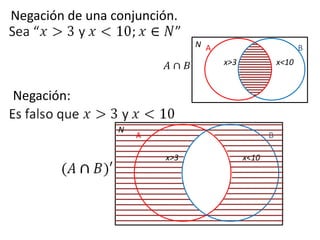
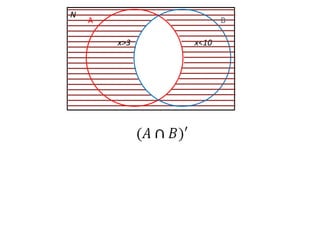
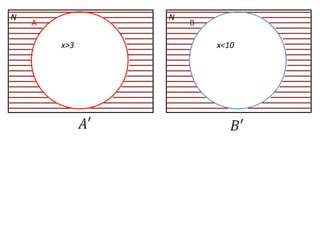
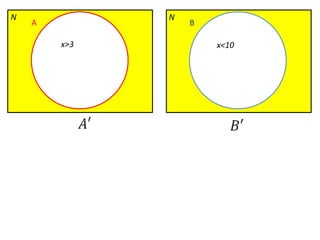
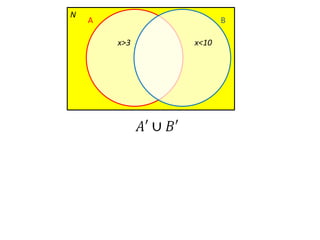
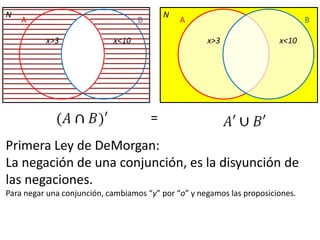
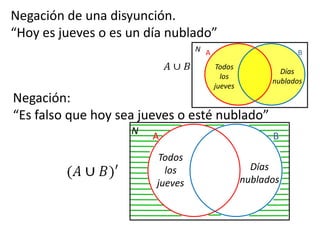
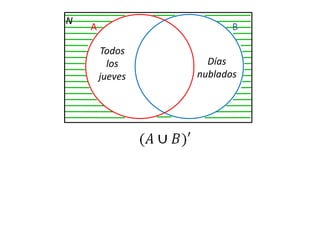
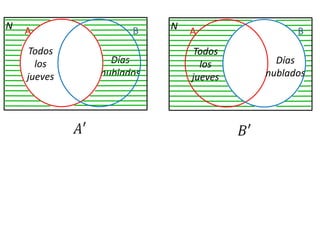
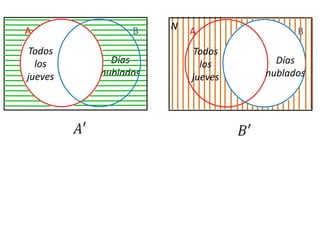
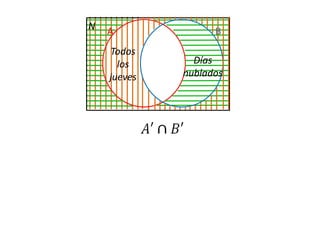
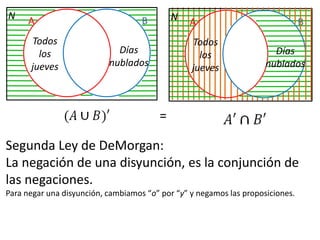
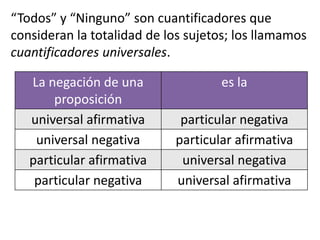
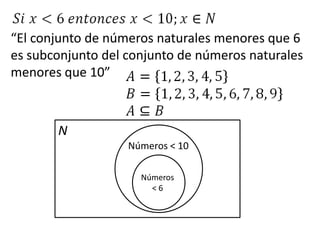
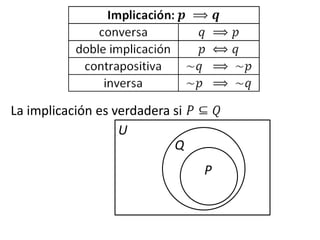
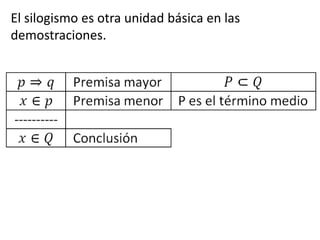
Este documento presenta conceptos básicos de lógica matemática como razonamiento inductivo y deductivo, proposiciones simples y compuestas, conjunción, disyunción, negación, implicación y reglas de inferencia. También introduce silogismos y la estructura básica de una demostración matemática.

1. El presente material debe ser considerado únicamente como un complemento para el estudio y de ninguna manera sustituye al libro de texto. MATEMÁTICAS I UNIDAD II ELEMENTOS DE LÓGICA MATEMÁTICA Contacto: joelamparn@gmail.com

2. Razonamiento inductivo: es el proceso de encontrar un principio general basándose en la presentación de hechos o casos específicos. Razonamiento deductivo: proceso mediante el cual se hace uso de un principio general, aceptado como verdadero, para obtener una conclusión en un hecho o caso particular. El razonamiento matemático es eminentemente deductivo, se apoya en postulados y definiciones.

3. Proposición: oración de la que se puede decir si es verdadera o falsa. Proposición simple: se puede decir de inmediato si es verdadera o falsa tiene un valor de verdad. Proposición abierta: tiene alguna variable y un conjunto de reemplazamiento  tiene un conjunto de verdad.

4. “6 es un número par” “6 es un elemento del conjunto de número pares” Números pares 6

5. “Todo hombre es mortal” “El conjunto de todos los hombres es un subconjunto del conjunto de todos los mortales” Conjunto mortales Conjunto hombres

6. N Números pares

7. N Múltiplos de 4

8. Proposición compuesta: proposiciones simples asociadas mediante conectivos lógicos  “y”, “o”, “Si… entonces”. Conjunción: asociación de dos composiciones con el conectivo lógico “y”. Es verdadera si ambas proposiciones simples son verdaderas; Es falsa si una proposición o ambas son falsas.

9. “4 es un número par y 4 es un número natural” verdadero verdadero La conjunción es verdadera. “3 es un número natural y 3 es un número par” verdadero falso La conjunción es falsa. “5 es un número par y 5 es múltiplo de 4” falso falso La conjunción es falsa.

10. Solución: la intersección de con N A B Números mayores que 5 Números pares

11. Disyunción: asociación de dos composiciones con el conectivo lógico “o” (en matemáticas, la disyunción es inclusiva). Es verdadera si cualquiera de las proposiciones simples es verdadera; Es falsa si ambas proposiciones son falsas.

12. “4 es un número par o 4 es un número natural” verdadero verdadero La disyunción es verdadera. “3 es un número natural o 3 es un número par” verdadero falso La disyunción es verdadera. “5 es un número par o 5 es múltiplo de 4” falso falso La disyunción es falsa.

13. Solución: la unión de con N A B Números mayores que 5 Números pares

14. Negación de la oración “Hoy es un día nublado” Es falso que hoy es un día nublado Hoy no es un día nublado. Si la proposición dada es verdadera, entonces la negación es falsa (y viceversa). La negación es el conjunto complemento. Conjunto de todos los días claros Conjunto de todos los días nublados

15. Si la proposición dada es abierta, los diagramas de Venn son todavía más valiosos: Negación N La parte sombreada representa la solución. Múltiplos de 4

16. Negación N 3 Números mayores que 5 1 4 2 5

17. Negación N 3 Números mayores que 5 1 Observaciones La negación de la negación de una proposición dada es la proposición misma. Negar una proposición negativa es igual a enunciar la proposición afirmativa. 4 2 5

18. Negación de una conjunción. N Negación: A B x>3 x<10 N A B x>3 x<10

19. N A B x>3 x<10

20. N N A B x>3 x<10

21. N N A B x>3 x>3 x<10

22. N A B x>3 x<10

23. N A B x>3 x<10 N A B x>3 x<10 = Primera Ley de DeMorgan: La negación de una conjunción, es la disyunción de las negaciones. Para negar una conjunción, cambiamos “y” por “o” y negamos las proposiciones.

24. Negación de una disyunción. “Hoy es jueves o es un día nublado” N Negación: “Es falso que hoy sea jueves o esté nublado” A B Todos los jueves N Días nublados A B Todos los jueves Días nublados

25. N A B Todos los jueves Días nublados

26. N N A B A B Todos los jueves Todos los jueves Días nublados Días nublados

27. N A B A B Todos los jueves Todos los jueves Días nublados Días nublados

28. N A B Todos los jueves Días nublados

29. N A B N A B Todos los jueves Todos los jueves Días nublados Días nublados = Segunda Ley de DeMorgan: La negación de una disyunción, es la conjunción de las negaciones. Para negar una disyunción, cambiamos “o” por “y” y negamos las proposiciones.

30. “Todos” y “Ninguno” son cuantificadores que consideran la totalidad de los sujetos; los llamamos cuantificadores universales.

31. Implicación: dos proposiciones unidas por el conectivo lógico “Si… entonces”. Si p entonces q p es la suposición o hipótesis, q es la conclusión. Forma simbólica:

32. “El conjunto de números naturales menores que 6 es subconjunto del conjunto de números naturales menores que 10” N Números < 10 Números < 6

33. La implicación es verdadera si U Q P

34. El valor de verdad de la conversa no se deduce del valor de verdad de la implicación. El valor de verdad de la doble implicación es verdadero si es verdadera la implicación y la conversa.

35. La contrapositiva es equivalente a la implicación. La inversa es equivalente a la conversa.

36. Reglas de inferencia: argumentaciones válidas en forma de implicaciones. Ejemplo (regla de la cadena): Si x es elemento del conjunto R, entonces x es elemento del conjunto S. Si x es elemento del conjunto S, entonces x es elemento del conjunto T. Conclusión: Si x es elemento del conjunto R, entonces x es elemento del conjunto T. hipótesis conclusión

37. El silogismo es otra unidad básica en las demostraciones.

38. Premisa mayor: Si un número es múltiplo de 6, entonces es múltiplo de 2 Premisa menor: 18 es múltiplo de 6 Conclusión: 18 es múltiplo de 2

39. Premisa mayor: Si un animal es un oso entonces le gusta la miel Premisa menor: A mi animal preferido le gusta la miel Conclusión: Mi animal preferido es un oso La demostración matemática exige apoyar con una o varias razones cada afirmación que se haga.

40. Demostración a dos columnas: pruebe que 33,210 es múltiplo de 45

41. Tomado de: Matemáticas I, Libro de Texto, SEP, Autores: Mario Villegas Urquidi, Francisco René Zubieta.