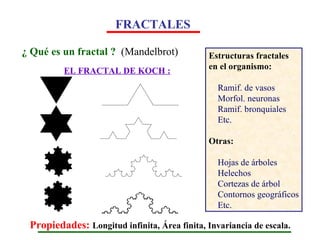
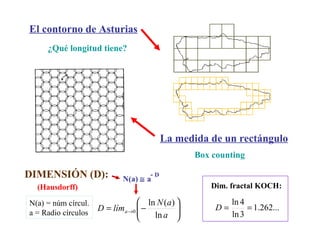
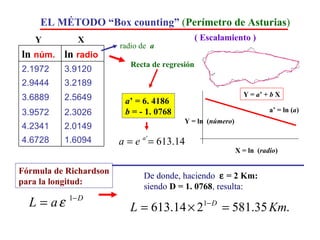
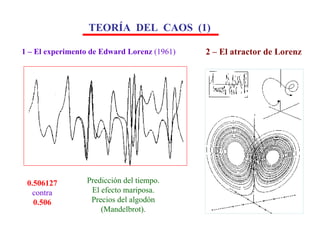
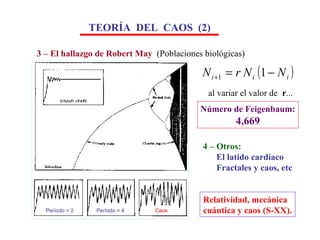
El documento aborda la intersección entre matemáticas y cáncer, destacando la importancia de los modelos matemáticos en la representación y predicción del crecimiento tumoral y la metástasis. Se discuten diferentes tipos de modelos, incluidos determinísticos y estocásticos, así como su aplicabilidad en el tratamiento y la comprensión de la dinámica de las células cancerosas. Además, se enfatiza la necesidad de integrar las matemáticas en la investigación médica para avanzar en el entendimiento del cáncer.

1. X CONGRESO Logroño, 12 al 14 de mayo 2011 MATEMÁTICAS Y CÁNCER Esquema general Introducción al tema Modelos matemáticos de aplicación 1) Clásicos 2) Modernos Geometría fractal Teoría del caos Matemática genética y cáncer Conclusiones actualizadas

2. ¿Qué se le puede pedir a un Modelo Matemático? Que represente la realidad, lo más fielmente posible. Para ello: Buena elección del tipo de modelo. Correcto planteamiento. Adecuada formulación. Posibilidades de resolución. Aplicabilidad. TIPOS DE MODELOS MATEMÁTICOS: Modelos determinísticos y estocásticos. Modelos continuos y discretos. Modelos matemáticos en tumores: a) Clásicos: Exponencial, Logístico, de Von Bertalanffy, de Gompertz … (Hay muchos de ellos) b) Actuales: de Brú, de Murray. (Otros) Modelos de cantidad de células y modelos de ciclo celular. MATEMÁTICAS Y CÁNCER Las Variables Tiempo Espacio

3. CRECIMIENTO DE POBLACIONES 1 – MALTHUS (1798) Curva exponencial 2 – VERHULST (1838) Curva logística 3 – VOLTERRA – LOTKA (1925) “De las dos especies” EJPLO DE APLICACIONES: Crecimiento y propagación de tumores, Id. de bacterias, Estudios genéticos varios, Inmunología, etc. Surgieron estos estudios con motivo del tema de la reproducción de los animales (Fibonacci, “ La isla de los conejos ”, S-XIII) t y Curva exponencial Curva logística Capacidad de carga y t K

4. MODELO EXPONENCIAL t C Quimio: Si destruye el 95 % de células por sesión, Precisan 7 sesiones para que quede una célula en un tumor de 10 células inicialmente. ( Condiciones determinadas) Aquí  sería negativo e igual a – 3 . 10 lo que implica: Tasa de crecimiento,  Si tiempo duplicación = 3 meses, podemos escribir:

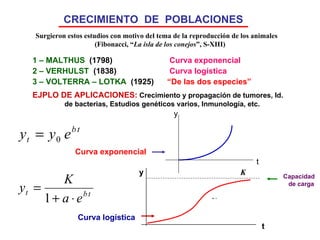
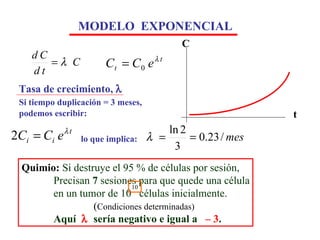
5. MODELO LOGÍSTICO EJPLO.- Tomando un a = 0.08 / mes y un b = 0.003 , K = 26.7 por tanto. Entonces el tiempo de duplicación sería: El máximo de [1] para t =  , sería K = 26.7 veces el volumen del tumor detectado en el tiempo t = 1. ( T. cerebrales, p. ej.) lo que implica: t = 9.16 meses [1] Con K = a / b (Elemento de freno) y t a = tasa de crecimiento b = coeficiente de densidad K

6. MODELO DE Von BERTALANFFY Aquí conviene calcular y en función de t , mediante la construcción de tablas. Para a = 0.25/mes y b = 0.1, el tiempo de duplicación resulta ser igual a 16 meses. El máximo volumen del tumor, para t =  , sería igual a 1 / b. (El factor de “freno” es ahora b y ) t y

7. MODELO DE GOMPERTZ (Cuando f (  ) decrece exponencialmente con el tiempo, tenemos la clásica función de Gompertz.) Siendo k = e a t y Familia de distribuciones de Gompertz: con  constante o no .

8. Transformación Angiogénesis Motilidad e invasión Embolismo circul . Adherencia Detención en lecho capilar Extravasación en parenquima Reacción al entorno Proliferación tumoral y angiogénesis Trasporte Agregación cel. Metástasis Metástasis de metástasis Capilares, vénulas, etc Extensión espacial MODELO DE METÁSTASIS

9. Se conocen más de un millar de modelos matemáticos para el crecimiento en número de las células cancerosas, lo que puede significar que: a) Hay muchas variedades de tumores. b) Tienen defectos casi todos los modelos. c) Varía el tipo de modelo en los diferentes estadíos del tumor. d) Es difícil la determinación de los parámetros. e) Intervienen otros factores propios del paciente. Etc. No todas las ecuaciones diferenciales se pueden solucionar directamente, siendo preciso recurrir a métodos numéricos en muchas ocasiones. Hasta ahora sólo hemos tenido en cuenta la evolución temporal de los tumores, pero no su difusión espacial. (Crecimiento, metástasis) Veremos más adelante otros tipos de modelos que intentan obviar estas dificultades. (James D. Murray, el propuesto por Antonio Brú, etc). CRÍTICA A LO HASTA AHORA DICHO

10. Tumor de 8  3  2.5 cm. Se extirpa, pero quedan: 3 cc locales y 15 metástasis de 0.75 cc en promedio (subclínicas). Volumen de las metástasis = 15  0.75 = 11.25 cc. De acuerdo con con lo dicho, proceden los siguientes cálculos: (Modelo Exponencial simple) EJEMPLO (1) Vol. Inic. del tumor : (Aquí = 31.4 cc.) Tiempos de duplicación: Tumor = 3 meses ; Metas = 2 meses. O sea: Suponiendo que 1 cc contiene 10 9 células tumorales, tenemos: Número de células del tumor = 3  10 9 Núm. células de las metas = 11.25  10 9

11. Si una sesión de “quimio” deja “vivas” al 5 % de células del tumor y al 2 % de células de las metástasis, resultará: Con lo que podemos confeccionar la siguiente tabla: EJEMPLO (2) Núm. de células tumorales tras la 1ª sesión de quimio: 0.15  10 9 = 15  10 7 Núm. de células de las metas tras la 1ª sesión de quimio: 9 0.225  10 = 22.5  10 7 Núm. de células tumorales 14 días después: Núm. de células de las metas 14 días después: Etc. N t 0 14

12. NOTA.- Es de destacar el componente aleatorio en las últimas sesiones. Tras la sesión de quimio Núm. de células del tumor Núm. de células de las metas 14 días después: Núm. células Núm. de células del tumor de las metas 1 ª 15  10 7 22.5  10 7 16.8  10 7 26.8  10 7 2 ª 84  10 5 54  10 5 94.5  10 5 63.6  10 5 3 ª 4.72  10 5 1.27  10 5 5.30  10 5 1.52  10 5 4 ª 26.5  10 3 3  10 3 29.8  10 3 3.6  10 3 5 ª 14.9  10 2 72 16.7  10 2 86 6 ª 83.5 1.71 93.7 2.04 7 ª 4.7 0.04 5.3 0.05 8 ª 0.26 0.001 0.30 0.001 9 ª 0.01 0.00002 0.02 0.00003 1 0 ª 0.0008 0 0.0009 0 EJEMPLO (3)

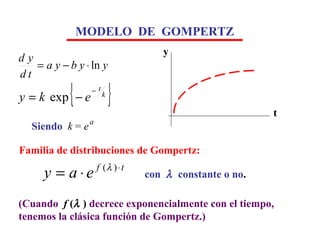
13. Más aun: ¿Cuando empezó el tumor del ejemplo? Resolviendo la ecuación , resulta : t = 104.63 meses = 8.72 años. Otra pregunta: ¿Cuándo se hizo “clínico” el tumor? ¡ Los comentarios surgen solos ! (Podemos intentar, ciertamente, modificar el modelo) ? ? EJEMPLO (4) Recordemos: Se hace clínico cuando su volumen es 1 cc. (= células) Al principio, Como  = 0.231 y En ese caso escribimos: que resuelta da: t = 89.71 meses = 7.5 años. [¿Gompertz?]

14. EJEMPLO (final) NOTA 1.- El mismo tumor, con un modelo Gompertz de crecimiento, con parámetro  de 0.05 al mes, habría comenzado 8 meses antes de su diag- nóstico, ¡Y no, hace más de 8 años! NOTA 3.- En el nuevo contexto, tras la 8 ª sesión de quimioterapia ya no quedaría activa ninguna célula del tumor (parecidamente al ejemplo). NOTA 4.- Acerca de las metástasis no estamos en condiciones de estimar en qué momento se iniciaron, en el caso de suponer que el modelo sigue la distribución de Gompertz. NOTA 5.- Los modelos matemáticos, si son acertados y se pueden estimar sus parámetros con la suficiente aproximación, constituyen una valiosa ayuda para el conocimiento de la dinámica de las células tumorales. NOTA 2.- Se evidencia la conveniencia de cambiar de modelo o de utilizar simultánea o sucesivamente, en este caso y en otros, dos o varios modelos diferentes.

15. DINÁMICA UNIVERSAL DE CRECIMIENTO TUMORAL (Antonio Brú & al.) FUNDAMENTOS: - MBE (Molecular beam epitaxy) - Crecimiento en superficie (interface) - Dimensiones fractales del borde - Similitud de tumor y metástasis Scaling analysis x = extensión del tumor t = tiempo de desarrollo K = coef. de distrib. en superficie F = tasa de crecimiento  = “ruido aleatorio” CRÍTICA

16. Parámetros:  = tasa de crecimiento D = coef. difusión espacial Valores: c ( x,t ) =Núm. células neoplásicas en la posición x y en el tiempo t . . . MODELO DE J. D. MURRAY (1) Solución : N = Núm cél. tum en t = 0 r = radio tumoral medio 0 Fase de establecimiento ( Te ): tiempo entre inicio y detección del tumor. Se cumple: lo que implica: con Tiempo de supervivencia ( Ts ):

17. 1 – Soporte de conocimientos médicos. 2 – Modelos matemáticos básicos. 3 – Diseminación tumoral “in vitro”. 4 – Diseminación en animales de experimentación. 5 – Diseminación en seres humanos. 6 – Ensayo de diversos tipos de tratamientos. 7 – Caso particular de la cirugía. 8 – Recurrencia de tumores. 9 – Caso de tejidos heterogéneos. 10 – Modelos aplicables a la quimioterapia. 11 – Caso de policlonalidad celular. (Un verdadero modelo de diseño experimental) Swanson, K.R; Alvord Jr, E.C; Woodward, D.E; Cook, J; Tracqui, P; Cruywagen, G.C; Bridge, C; etc. . . . MODELO DE J. D. MURRAY (2) ASPECTOS A CONSIDERAR (“Pasos”)

18. Propagación espacial MODELO DE J. D. MURRAY (3) 1 – Paseo aleatorio Prob. de alcanzar el punto m tras n pasos = (Distrib. normal) 2 – Ecuación de ondas D = coef. difusión C = núm. células Cuya solución es: Q = Partículas por unidad de área, con x = 0 y t = 0. (Eqs. en derivadas parciales) 3 – Ecuación de Fisher-Kolmogorov ( Forma más simple ) Cuya solución es: u = concentración; c = Velocidad de propagación de la onda viajera; a , A = constantes. (Deriv. parciales) P m

19. ¿ Qué es un fractal ? (Mandelbrot) EL FRACTAL DE KOCH : Estructuras fractales en el organismo: Ramif. de vasos Morfol. neuronas Ramif. bronquiales Etc. Otras: Hojas de árboles Helechos Cortezas de árbol Contornos geográficos Etc. FRACTALES Propiedades: Longitud infinita, Área finita, Invariancia de escala.

20. Un Fractal Geométrico: el triángulo de Sierpinski MEDIDA del área no blanqueada = CERO

21. UN FRACTAL GEOMÉTRICO CARACTERÍSTICO (Juliá)

22. El contorno de Asturias La medida de un rectángulo ¿Qué longitud tiene? Box counting DIMENSIÓN (D): (Hausdorff) N(a) = núm círcul. a = Radio círculos N(a)  a - D Dim. fractal KOCH:

23. X = ln ( radio ) Y = ln ( número ) Y = a ’ + b X a’ = ln ( a ) a ’ = 6. 4186 b = - 1. 0768 Recta de regresión X Y De donde, haciendo  = 2 Km: siendo D = 1. 0768 , resulta: radio de a ( Escalamiento ) EL MÉTODO “Box counting” ( Perímetro de Asturias ) 1.6094 4.6728 2.0149 4.2341 2.3026 3.9572 2.5649 3.6889 3.2189 2.9444 3.9120 2.1972 ln radio ln núm. Fórmula de Richardson para la longitud:

24. TEORÍA DEL CAOS (1) 1 – El experimento de Edward Lorenz (1961) 0.506127 contra 0.506 Predicción del tiempo. El efecto mariposa. Precios del algodón (Mandelbrot). 2 – El atractor de Lorenz

25. TEORÍA DEL CAOS (2) 3 – El hallazgo de Robert May (Poblaciones biológicas) al variar el valor de r ... Número de Feigenbaum: 4,669 4 – Otros: El latido cardíaco Fractales y caos, etc Relatividad, mecánica cuántica y caos (S-XX). Período = 2 Período = 4 Caos

26. MATEMÁTICA GENÉTICA 1 – Caminos aleatorios y ADN Purinas: Adenina, Guanina. Pirimidinas: Citosina, Timina. Regla Purina-pirimidina: Pirimidina: arriba, Purina: abajo. 3 – Papel posible del caos. 2 – Perfil fractal (Paisajes) Rugosidad unida a NO codificación. a) Gran parte de zonas que no codifican. b) Sólo las zonas que codifican. c) Secuencia de bacteriófago: sólo zonas que codifican.

27. 1.- Las Matemáticas deben entrar a formar parte de los equipos multidisciplinares que se ocupan de Investigación Básica en Ciencias de la Salud. 2.- Hoy día todavía no pueden resolver las Matemáticas los problemas que plantean el cáncer y otras dolencias, pero ya suponen una ayuda notable. 3.- Así como la Bioquímica ha tenido un papel fundamental en Medicina, es ya el tiempo en que las Matemáticas han de asumir un protagonismo básico en Ciencias de la Vida. 4.- La investigación biomatemática en determinadas disciplinas, …. como la genética, por ejemplo, requiere que el investigador …. posea un conocimiento notable de ambas materias. CONCLUYENDO ...

28. X CONGRESO Logroño, 12 al 14 de mayo 2011 m i g u e l . a n d e r i z @ u n a v a r r a . e s MATEMÁTICAS Y CÁNCER Muchas gracias por su atención