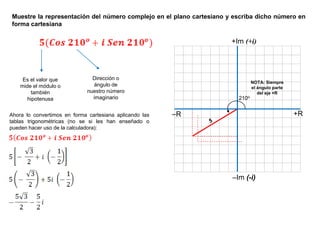
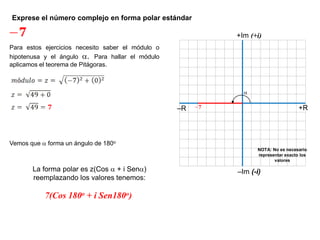
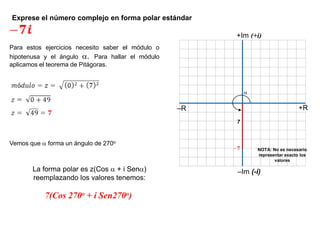
El documento explica cómo representar números complejos geométricamente en un plano cartesiano y cómo convertir entre las formas cartesiana y polar de un número complejo. Se muestran ejemplos de números complejos dados y sus representaciones correspondientes en el plano, y cómo calcular el módulo, ángulo y conversión a forma polar. También se discuten identidades trigonométricas para operaciones con números complejos.

2. Muestre la representación geométrica del número complejo como un punto en el plano complejo
1). 7 – 8i
2). –4 + 9i
3). –3 – i
4). 3i
+R–R
–Im (-i)
+Im (+i)
7 – 8i
– 4 + 9i
– 3 – i
3i
En estos ejercicios el valor que
NO lleva “i” se lo reemplaza en el
eje de las “x” o (R) y el valor que
lleva la “i” se lo reemplaza en el
eje de las “y” o (Im)
9
-4 -3 7
-8

3. Determine el valor absoluto indicado
Este también se lo conoce como módulo, y es la aplicación del Teorema de Pitágoras, tomando solo los valores
numéricos del número imaginario
+R–R
–Im (-i)
+Im (+i)

4. Muestre la representación del número complejo en el plano cartesiano y escriba dicho número en
forma cartesiana
Es el valor que
mide el módulo o
también
hipotenusa
Dirección o
ángulo de
nuestro número
imaginario
+R–R
–Im (-i)
+Im (+i)
210o
NOTA: Siempre
el ángulo parte
del eje +R
Ahora lo convertimos en forma cartesiana aplicando las
tablas trigonométricas (no se si les han enseñado o
pueden hacer uso de la calculadora):

5. Muestre la representación del número complejo en el plano cartesiano y escriba dicho número en
forma cartesiana
Es el valor que
mide el módulo o
también
hipotenusa
Dirección o
ángulo de
nuestro número
imaginario
+R–R
–Im (-i)
+Im (+i)
-2/3
180o
NOTA: Siempre
el ángulo parte
del eje +R
Ahora lo convertimos en forma cartesiana aplicando las
tablas trigonométricas (no se si les han enseñado o
pueden hacer uso de la calculadora):

6. Muestre la representación del número complejo en el plano cartesiano y escriba dicho número en
forma cartesiana
Es el valor que
mide el módulo o
también
hipotenusa
Aquí debo
convertir los 
radianes a
grados
+R–R
–Im (-i)
+Im (+i)
-1/2
270o
NOTA: Siempre
el ángulo parte
del eje +R
Ahora lo convertimos en forma cartesiana aplicando las
tablas trigonométricas (no se si les han enseñado o
pueden hacer uso de la calculadora):
 = 180o

7. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)

NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.

 = + 90o
Aplicando las funciones trigonométricas aplico tangente para
hallar . Sabemos q la función tangente es igual a opuesto sobre
adyacente, con respecto a  el opuesto es el valor de R y el
adyacente el valor de “i”, entonces:
 = + 90o
 =60o + 90º = 150o
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
6(Cos 150o + i Sen150o)

8. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)

NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.
Vemos que  forma un ángulo de 180o
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
7(Cos 180o + i Sen180o)

9. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)
7

NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.
Vemos que  forma un ángulo de 270o
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
7(Cos 270o + i Sen270o)

10. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)

NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
Aplicando las funciones trigonométricas aplico tangente para
hallar . Sabemos q la función tangente es igual a opuesto sobre
adyacente, con respecto a  el opuesto es el valor de R y el
adyacente el valor de “i”, entonces:
 = + 270o
 = + 270o
 =45o + 270o
 = 315o

11. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)
NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.
Vemos que  forma un ángulo de 0o
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
5(Cos 0o + i Sen 0o)

12. Exprese el número complejo en forma polar estándar
+R–R
–Im (-i)
+Im (+i)
NOTA: No es necesario
representar exacto los
valores
Para estos ejercicios necesito saber el módulo o
hipotenusa y el ángulo . Para hallar el módulo
aplicamos el teorema de Pitágoras.
Vemos que  forma un ángulo de 90o
La forma polar es z(Cos  + i Sen)
reemplazando los valores tenemos:
5(Cos 90o + i Sen 90o)


13. Exprese el producto en forma cartesiana
Aquí debo convertir los 
radianes a grados
 = 180o
Debo usar identidades trigonométricas:
Sen ( + ) = Sen. Cos + Cos Sen
Cos ( + ) = Cos. Cos + Sen Sen

14. Exprese el producto en forma cartesiana
Debo usar identidades trigonométricas:
Sen ( + ) = Sen. Cos + Cos Sen
Cos ( + ) = Cos. Cos + Sen Sen

15. Exprese el cociente en forma cartesiana
Debo usar identidades trigonométricas:
Sen ( + ) = Sen. Cos + Cos Sen
Cos ( + ) = Cos. Cos + Sen Sen
Cos2  + Sen2  = 1