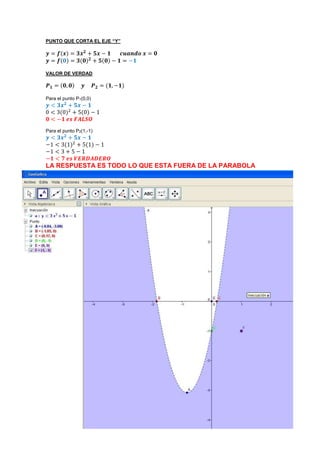
Este documento resuelve una desigualdad cuadrática y encuentra su región de solución. Primero, simplifica la desigualdad hasta reducirla a (x + 5/6)2. Luego, calcula el vértice en (-5/6, -37/12) y los puntos donde corta el eje x en aproximadamente 0.18 y 1.85. Finalmente, verifica que el punto (0,0) está fuera de la región mientras que (1,-1) está dentro.

1. 𝒚 < 𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏
𝑦
3
<
3𝑥2
3
+
5𝑥
3
−
1
3
𝑦
3
< 𝑥2
+
5𝑥
3
−
1
3
𝑦
3
+
37
36
< 𝑥2
+
5𝑥
3
−
1
3
+
37
36
𝑦
3
+
37
36
< 𝑥2
+
5𝑥
3
+
25
36
𝑦
3
+
37
36
< (𝑥 +
5
6
)
2
PUNTOS DEL VÉRTICE
𝑦
3
+
37
36
= 0
𝑦
3
= −
37
36
𝑦 = −
37(3)
36
= −
𝟑𝟕
𝟏𝟐
≅ −𝟑. 𝟎𝟖
𝑽(𝒉, 𝒌)
𝑽 (−
𝟓
𝟔
, −
𝟑𝟕
𝟏𝟐
)
PUNTOS QUE CORTA EL EJE “X”
𝒚 = 𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏
𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏 = 𝟎 𝒂 = 𝟑, 𝒃 = 𝟓, 𝒄 = −𝟏
𝑥 =
−𝑏 ± √𝑏2 − 4𝑎𝑐
2𝑎
=
−5 ± √(5)2 − 4(3)(−1)
2(3)
=
−5 ± √25 + 12
6
𝑥 =
−5 ± √37
6
𝑥1 =
−5 + √37
6
≅ 𝟎. 𝟏𝟖 𝑥2 =
−5 − √37
6
≅ 𝟏, 𝟖𝟓
(𝑥 +
5
6
)
2
= 0
√(𝑥 +
5
6
)
2
= √0
𝑥 +
5
6
= 0
𝑥 = −
5
6
≅ 𝟎. 𝟖𝟑

2. PUNTO QUE CORTA EL EJE “Y”
𝒚 = 𝒇(𝒙) = 𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏 𝒄𝒖𝒂𝒏𝒅𝒐 𝒙 = 𝟎
𝒚 = 𝒇(𝟎) = 𝟑(𝟎) 𝟐
+ 𝟓(𝟎) − 𝟏 = −𝟏
VALOR DE VERDAD
𝑷 𝟏 = (𝟎, 𝟎) 𝒚 𝑷 𝟐 = (𝟏, −𝟏)
Para el punto P1(0,0)
𝒚 < 𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏
0 < 3(0)2
+ 5(0) − 1
𝟎 < −𝟏 𝒆𝒔 𝑭𝑨𝑳𝑺𝑶
Para el punto P2(1,-1)
𝒚 < 𝟑𝒙 𝟐
+ 𝟓𝒙 − 𝟏
−1 < 3(1)2
+ 5(1) − 1
−1 < 3 + 5 − 1
−𝟏 < 𝟕 𝒆𝒔 𝑽𝑬𝑹𝑫𝑨𝑫𝑬𝑹𝑶
LA RESPUESTA ES TODO LO QUE ESTA FUERA DE LA PARABOLA