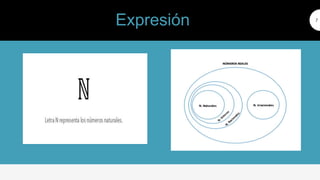
Este documento trata sobre los números naturales, reales y operaciones con conjuntos y números. Explica que los números naturales son los primeros números que aprendemos y no incluyen el cero. Luego define los números reales como cualquier número en la recta real y clasifica los números reales en naturales, enteros, racionales e irracionales. Finalmente, describe operaciones básicas con conjuntos y números como unión, intersección y suma/resta de fracciones.

1. NÚMEROS
NATURALES
Alejandro Ramírez
C.I 28.220.513
MINISTERIO DE EDUCACION SUPERIOR
Universidad Politécnica Territorial de Lara
Andrés Eloy Blanco
BARQUISIMETO EDO-LARA

2. • Un conjunto lo forman unos elementos de la misma
naturaleza, es decir, elementos diferenciados entre sí pero
que poseen en común ciertas propiedades o características,
y que pueden tener entre ellos, o con los elementos de
otros conjuntos, ciertas relaciones.
• Un conjunto puede tener un número finito o infinito de
elementos, en matemáticas es común denotar a los
elementos mediante letras minúsculas y a los conjuntos
por letras mayúsculas, así por ejemplo:
• C = {a, b, c, d, e, f, g, h}
2
• En ocasiones un conjunto viene expresado por la
propiedad (o propiedades) que cumplen sus
elementos, por ejemplo:
• es el conjunto de los números reales comprendidos
entre el 1 y el 2 ( incluidos ambos).
• Dos conjuntos A y B son iguales, expresado A = B,
solamente cuando constan de los mismos elementos.
Conjunto

3. • Operaciones con conjuntos.
• Las operaciones con conjuntos también conocidas como
álgebra de conjuntos, nos permiten realizar operaciones
sobre los conjuntos para obtener otro conjunto. De las
operaciones con conjuntos veremos las siguientes: unión,
intersección, diferencia, diferencia simétrica y
complemento.
• Unión o reunión de conjuntos.
• Es la operación que nos permite unir dos o más conjuntos
para formar otro conjunto que contendrá a todos los
elementos que queremos unir pero sin que se repitan.
3
• Ejemplo 1.
• Dados dos conjuntos A={1,2,3,4,5,6,7,} y B={8,9,10,11} la
unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9,10,11}
• . Ejemplo 2.
• Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
unión de estos conjuntos será A∪B={1,2,3,4,5,6,7,8,9}.
•
Operación con conjuntos

4. • ‒ Intersección de conjuntos.
• Es la operación que nos permite formar un conjunto, sólo
con los elementos comunes involucrados en la operación.
Es decir dados dos conjuntos A y B, la de intersección de
los conjuntos A y B, estará formado por los elementos de A
y los elementos de B que sean comunes, los elementos no
comunes A y B, será excluidos. El símbolo que se usa para
indicar la operación de intersección es el siguiente: ∩
• Ejemplo 1.
• Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
intersección de estos conjuntos será A∩B={4,5}. Usando
diagramas de Ven se tendría lo siguiente:
4
Intersección De Conjuntos

5. • Es la operación que nos permite formar un conjunto, en
donde de dos conjuntos el conjunto resultante es el que
tendrá todos los elementos que pertenecen al primero pero
no al segundo. Es decir dados dos conjuntos A y B, la
diferencia de los conjuntos entra A y B, estará formado por
todos los elementos de A que no pertenezcan a B. El
símbolo que se usa para esta operación es el mismo que se
usa para la resta o sustracción, que es el siguiente: -
• Ejemplo 1.
• Dados dos conjuntos A={1,2,3,4,5} y B={4,5,6,7,8,9} la
diferencia de estos conjuntos será A-B={1,2,3}. Usando
diagramas de Ven se tendría lo siguiente:
5
Diferencia De Conjuntos

6. • Los números reales son cualquier número que
corresponda a un punto en la recta real y pueden
clasificarse en números naturales, enteros, racionales e
irracionales. Los números reales se representan mediante la
letra R ↓
• los números reales son los números comprendidos entre los
extremos infinitos. Es decir, no incluiremos estos infinitos
en el conjunto.
6
• Clasificación de los números reales
• Tal y como hemos visto, los números reales pueden
clasificarse entre números naturales, enteros, racionales e
irracionales. Números naturales
• Los números naturales es el primer conjunto de números que
aprendemos de pequeños. Este conjunto no tiene en cuenta el
número cero (0) excepto que se especifique lo contrario (cero
neutral).
Números Reales

7. 7
Expresión

8. • Los números enteros son todos los números naturales e
incluyen el cero (0) y todos los números negativos.
• Expresión:
8
ros racionales
• Los números racionales son las fracciones que pueden
formarse a partir de los números enteros y naturales.
Entendemos las fracciones como cocientes de números
enteros.
• Expresión:
Números Enteros Y Racionales

9. Adición y Sustracción en Q
• Primer Caso: Cuando tienes iguales denominadores se
suman o se restan los numeradores entre si y el resultado
se escribe como numerador y como denominador se
escribe el mismo denominador de la fracción.
• Segundo Caso: Cuando la fracción tiene diferente
denominadores se haya el mínimo como un
denominador y luego se procede como en el caso
anterior.
9
• Ejemplo 1:
• 5 + 3 + 1= 5 + 3 + 1= 9
4 4 4 4 4
• Ejemplo 2:
• 1 + 2 + 5 = 3 + 8 + 30 = 41
4 3 2 12 12
• Ejemplo 3:
• 7 – 1 = 7 – 3 = 4 = 1
12 4 12 12 3
Operaciones en Q

10. • Multiplicación en Q: El producto de dos o mas números
racionales será otro racional que tiene por numerador al
producto de los numeradores y por denominador al
producto de los denominadores
• División en Q: el cociente de la fracción a/b entre c/d
≠0, es otra fracción que se obtiene al multiplicar a/b por
el inverso del divisor d/c
Así: a
b = a.d
c b.d
d
10
• Ejemplo 1:
• 2 . 1 . 6 = 12 = 4 = 1
3 4 5 60 20 5
• Ejemplo 2:
• 5
14 = 5.3 = 15
7 14.7 98
3
Operaciones en Q

11. • Los números irracionales son números
decimales que no pueden expresarse ni de
manera exacta ni de manera periódica.
• Expresión:
11
Números Irracionales

12. • una desigualdad es una relación de orden que se da entre dos
valores cuando estos son distintos
• Si los valores en cuestión son elementos de un conjunto ordenado,
como los enteros o los reales, entonces pueden ser comparados.
• La notación a < b significa a es menor que b;
• La notación a > b significa a es mayor que b
• Estas relaciones se conocen como desigualdades estrictas, puesto
que a no puede ser igual a b; también puede leerse como
"estrictamente menor que" o "estrictamente mayor que".
• La notación a ≤ b significa a es menor o igual que b;
• La notación a ≥ b significa a es mayor o igual que b;
12
• estos tipos de desigualdades reciben el nombre de desigualdades
amplias (o no estrictas).
• Propiedades de la desigualdad matemática
• Si se multiplica ambos miembros de la expresión por el mismo valor,
la desigualdad se mantiene.
• Si dividimos ambos miembros de la expresión por el mismo valor, la
desigualdad se mantiene.
• Si restamos el mismo valor a ambos miembros de expresión, la
desigualdad se mantiene.
• Si sumamos el mismo valor a ambos miembros de la expresión, la
desigualdad se mantiene.
Desigualdades

13. • Hay que tener presente que las desigualdades
matemáticas poseen también las siguientes
propiedades:
• Si se multiplica ambos miembros de la expresión por
un número negativo, la desigualdad cambia de
sentido.
• Si se divide ambos miembros de la expresión por un
número negativo, la desigualdad cambia de sentido.
13
Desigualdades

14. • Inecuaciones de primer grado:
• Hallar la solución de la siguiente desigualdad:
• 3(x – 2) ≤ 5x + 2
3(x – 2) ≤ 5x + 2
3x – 6 ≤ 5x + 2 + 6
3x – 6 + 6 ≤ 5x + 2 + 6
3x ≤ 5x + 8
3x – 5x ≤ 5x – 5x + 8
-2x ≤ 8
-2x ≥ 8
-2 -2
x ≥ -4
14
• Propiedad distributiva .
• Sumamos 6 en ambos miembros
• Simplificando
• Restamos 5x o sumamos -5x en ambos miembros
• Simplificando
• Dividimos por -2 (o multiplicamos por -2 e invertimos el sentido
de desigualdad ).
• Simplificando
Ejercicios

15. • Inecuaciones de segundo grado:
• 1) x² − 6x + 8 > 0
1º Igualamos el polinomio del primer miembro a cero y obtenemos
las raíces de la ecuación de segundo grado.
x² − 6x + 8 = 0
• Las soluciones son raíces reales distintas porque el discriminante
es mayor que cero (Δ > 0)
• 2º Representamos estos valores en la recta real. Tomamos un
punto de cada intervalo y evaluamos el signo en cada intervalo:
• Los puntos extremos están en blanco porque no pertenecen a la
solución, ya que no es mayor o igual
15
• P(0) = 0² − 6 · 0 + 8 > 0
• P(3) = 3² − 6 · 3 + 8 = 17 − 18 < 0
• P(5) = 5² − 6 · 5 + 8 = 33 − 30 > 0
• 3º La solución está compuesta por los intervalos (o el
intervalo)
que tengan el mismo signo que el polinomio.
• Los intervalos son abiertos porque 2 y 4 no están incluidos en la
solución
• S = (–∞, 2) U (4, ∞)
Ejercicios

16. • Valor absoluto es el valor que tiene un número más allá de
su signo. Esto quiere decir que el valor absoluto, que
también se conoce como módulo, es la magnitud
numérica de la cifra sin importar si su signo es positivo o
negativo.
• Tomemos el caso del valor absoluto 5. Este es el valor
absoluto tanto de +5 (5 positivo) como de -5 (5 negativo).
El valor absoluto, en definitiva, es el mismo en el número
positivo y en el número negativo: en este caso, 5. Cabe
destacar que el valor absoluto se escribe entre dos barras
verticales paralelas; por lo tanto, la notación correcta es |5|.
16
• También se puede entender el valor absoluto como
la distancia que existe entre el número y 0. El número 563 y el
número -563 están, en una recta numérica, a la misma distancia
del 0. Ese, por lo tanto, es el valor absoluto de ambos: |563|.La
distancia que existe entre dos números reales, por otra parte, es
el valor absoluto de su diferencia. Entre 8 y 5, por ejemplo, hay
una distancia de 3. Esta diferencia tiene un valor absoluto de |3|
Valor Absoluto

17. • Como los valores positivos y negativos tienen un valor absoluto
positivo, resolver ecuaciones con valores absolutos significa
encontrar la solución para ambos valores positivo y negativo.
• Primero veamos un ejemplo básico.
• La ecuación dice “el valor absoluto de x es igual a cinco.” La
solución es el valor o valores que estás a cinco unidades a partir de 0
en la recta numérica.
• Podrías pensar inmediatamente en el 5; que es una solución de la
ecuación. Observa que −5 también es una solución porque −5 está a
5 unidades del 0 en la
17
• dirección opuesta. Entonces la solución a la ecuación es x = −5
o x = 5.
• Un problema más complejo de valor absoluto se resuelve de manera
similar. Considera Esta ecuación te pide encontrar qué
número mas 5 tiene un valor absoluto de 15. Como 15 y −15 tienen
valor absoluto de 15, la ecuación de valor absoluto es válida cuando
la cantidad x + 5 es 15 o x + 5 es −15, ya que |15|
• = 15 y |−15| = 15. Entonces, necesitas encontrar qué valor de x hará
la expresión igual a 15 así como qué valor de x hará la expresión
igual a −15. Resolviendo las dos ecuaciones obtienes:
Desigualdades Con Valor Absoluto

18. • http://www.ehu.eus/juancarlos.gorostizaga/apoyo/conjuntos.
htm
• https://www.conoce3000.com/html/espaniol/Libros/Matema
tica01/Cap10-03-
OperacionesConjuntos.php#:~:text=Las%20operaciones%2
0con%20conjuntos%20tambi%C3%A9n,diferencia%2C%2
0diferencia%20sim%C3%A9trica%20y%20complemento.
• http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Reales/
marco_reales.htm
• https://economipedia.com/definiciones/numeros-reales.html
18
• https://es.wikipedia.org/wiki/Desigualdad_matem%C3%A1tic
a
• https://economipedia.com/definiciones/desigualdad-
matematica.html
• https://definicion.de/valor-absoluto/
• https://www.montereyinstitute.org/courses/DevelopmentalMat
h/TEXTGROUP-9-
14_RESOURCE/U10_L3_T2_text_final_es.html
Revisión Bibliográfica