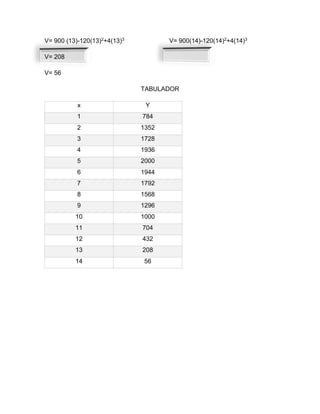
El documento describe los pasos para resolver problemas de optimización de áreas, incluyendo formular la función objetivo, establecer relaciones entre variables y sustituir variables para dejar una sola variable. Luego presenta dos ejemplos de problemas de optimización de áreas que siguen estos pasos: 1) encontrar las dimensiones óptimas de un envase cilíndrico de 255 ml y 2) determinar el tamaño óptimo de un corte en una caja de cartón para lograr el máximo volumen.

1. OPTIMIZACION DE AREAS
En la resolución de problemas de optimización de áreas seguiremos los siguientes
pasos:
1.- planear la función que hay que maximizar o minimizar.
2.- planear una ecuación que relacione las distintas variables del problema, en el
caso de que haya más de una variable.
3.- despejar una variable de la ecuación y sustituirla en la función en modo que
nos quede una sola variable.
EJEMPLO 1:
Un fabrícate necesita construir envases de lata de forma cilíndrica que contenga
un volumen de 255ml. Con el mínimo material posible por lo que necesita conocer
las dimensiones que deberá tener el envase para que cumpla con estas
condiciones.
Formulas: Área de una circunferencia. Área de
un rectángulo.
V= Π. 푟2. ℎ Π. 푟2 b. h
V=255ml. b X h
V=Π. 푟2. ℎ Π. 푟2
255= Π. 푟2. ℎ
A3
A1
A2

2. X Radio. Y Area.
Area= A1 + A2+ A3 0.5 4021.57
A= Π. 푟2+ b X h + Π. 푟2 1 516.28
A= Π. r + 2 Π r h + Π. 푟2 1.5 354.13
A= (3.14)푟2 + 2 (3.14) r (255/3.14푟2)+3.14푟2 2 280.12
Y= 3.14푥2+2(255) +3.14푥2 2.5 243.25
(3.14)(r) (2) (r) + (vol ÷ (3.14(푟2)) 3 226.52
4 222.64
4.5 227.98
(3.14)(1)(2(1)+ ((510÷(3.14(1)2)=516.28 5 259
Altura 5.5 282.69
6 311.08
H=255/(3.14) 1)2=81.21 Base=2(3.14)(1)=6.28
Radio= 1cm.
(3.14)(1.5)(1.5)+(510÷(3.14(15)2)=354.13
Altura
H=255/(π)(15)=36.09 Base: 2(π)(1.5)=9.42 Radio=1.5cm
(π)(2)(2(2)+(510÷(3.14(2)2=280.12
Altura Base= 2(π)(2)=12.56 Radio=2cm
H= 255

3. (π)(2.5)(2(2.5)+ (510÷(3.14(2)2)=280.12
Altura Base= 2(π)(2)=12.56
H=255
(π)(2.5)(2(2.5)+ (510÷(3.14(2.5)2)=243.25
Altura Base.
H=255/(π)(2.2.5)2=12.99 h= 255/(π)(2.5)32.48
(π)(3.5)(2(3.5)+ (510÷( (휋(4))=227.98
Altura h=255/(π)( 32)=9.02 Base= 2(π)(3.5)=21.98
(π)(4)(2(4)+ (510÷( (휋(4)2)=240.50 Base= 2(π)( 9.5)=28.26
Altura= h=255/(π)(4.5)=4.01
(π)(5)(2(5)+ 510÷(휋(5)2))=259 Base= 2(π)(5)=31.4
Altura h=255/(π)(5)2=3.24
(π)(5.5)(2(5.5)+ (510÷( (휋(5.5)2)=282.69
Altura h= 255/(π)(5.5)2=2.68 Base= 2(π)(6)=37.68
(π)(6)(2(6)+ (510÷( (휋(6)2)=311.08 Base= 2(π)(6)=37.68
Altura h= 222/π)(6)2=2.25

4. EJEMPLO 2:
Con una pieza pegada al cartón que mide 30 x 30 se quiere construir una caja
abierta cortando cuadros iguales en las esquinas y doblando hacia arriba. ¿Cuál
debe ser la longitud del lado x que se debe cortar para que la caja tenga un
volumen máximo?
V=LxLxL V=(30-2x)(30-2x)(x)
V=(900-60x-60x+4x2)(x)
V=(900-120x+4x2)(x)
formula V=900x-120x2+4x3
V= 900x -120x2+4x3
V= 900(1)-120(1)2+4(1)3
V= 784
V= 900(2)-120(2)2+4(2)3
V= 1352
V= 900(3)-120(3)2+4(3)3
V= 1728
V= 900(4)-120(4)2+4(4)3
V= 1936
V= 900(5)-120(5)2+4(5)3
V= 2000
V= 900(6)-120(6)2+4(6)3
V= 1944
V= 900(7)-120(7)2+4(7)3
V= 1792
V= 900(8)-120(8)2+4(8)3
V= 1568
V= 900(9)-120(9)2+4(9)3
V= 1299
V= 900(10)-120(10)2+4(10)3
V= 100
V= 900(11)-120(11)2+4(11)3
V= 704
V= 900(12) -120(12)2+4(12)3
V= 432

5. V= 900 (13)-120(13)2+4(13)3
V= 208
V= 900(14)-120(14)2+4(14)3
V= 56
TABULADOR
x Y
1 784
2 1352
3 1728
4 1936
5 2000
6 1944
7 1792
8 1568
9 1296
10 1000
11 704
12 432
13 208
14 56