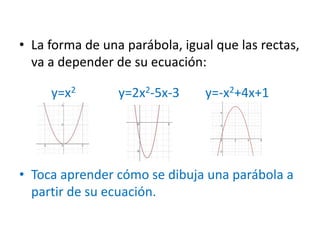
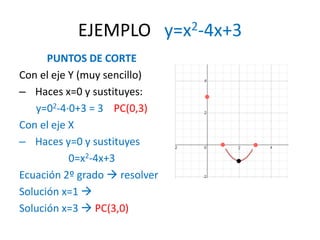
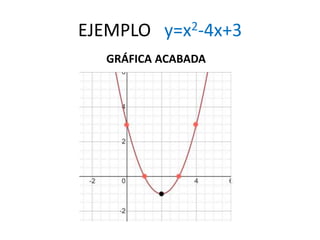
Este documento explica las parábolas y cómo graficarlas. Indica que una función cuadrática tiene la forma y=ax^2 + bx + c, donde a, b y c pueden ser cualquier número. Esto determina la orientación, vértice y puntos de corte de la parábola. Muestra un ejemplo de cómo graficar la parábola y=x^2 - 4x + 3 paso a paso determinando estos elementos y creando una tabla de valores. Finalmente, indica que a veces la ecuación puede no estar completa y que al resolver la ecuación de segundo gra

1. PARÁBOLA
Concepto y Gráfica
Sebastián Munuera. 2020

2. FUNCIONES CUADRÁTICAS. PARÁBOLAS
• Una función cuadrática tiene:
esta forma o esta o esta otra
Y cada una tiene su ecuación:
y=x2 y=2x2-5x-3 y=-x2+4x+1
(si por ahora no te suenan, no te preocupes)

3. y=x2 y=2x2-5x-3 y=-x2+4x+1
Estas gráficas se llaman PARÁBOLAS
La ecuación de una parábola tiene que tener
X2
Estas no lo son: y=x3-x2+x+1 y=3x-7

4. • Si recuerdas, las ecuaciones de todas las rectas
tenían la forma y=mn+n donde ´m´ y ´n´ pueden
ser números cualquiera:
y=2x+1 y=-3x-100 y=½ x+7 ………..
• Las ecuaciones de todas las parábolas tienen
esta forma:
y=ax2+bx+c
a, b y c pueden ser números cualquiera:
Ejemplo: y=2x2-5x-3  a=2, b=-5, c=-3

5. • La forma de una parábola, igual que las rectas,
va a depender de su ecuación:
y=x2 y=2x2-5x-3 y=-x2+4x+1
• Toca aprender cómo se dibuja una parábola a
partir de su ecuación.

6. • Hay un forma elemental, hacerlo igual que con
la recta:
– Con una tabla de valores.
– Para cada valor de ´x´, calcular el de ´y´.
– Dibujar los puntos, y unirlos.
• Este procedimiento tiene algún problema
– Necesito muchos más puntos que en la recta.
– Si la parábola está muy a la izquierda o a la
derecha, y yo empiezo por x=1, x=2, ….. me va a
salir algo muy raro (no lo pruebes).

7. • Para dibujar bien una parábola necesito tener
claro unos conceptos (es sencillo):
• VÉRTICE: es el punto donde
la parábola se da la vuelta.
• ORIENTACIÓN: es si la parábola
mira hacia arriba o hacia abajo
• PUNTOS DE CORTE: donde la
parábola corta a los ejes ´x´ o ´y´.

8. EJEMPLO y=x2-4x+3
• Recordando lo que hemos visto. Si todas las
parábolas tienen la forma y=ax2+bx+c
• Entonces: a=1, b=-4, c=3 (´a´ es el número del x2)
• El proceso tiene 4 pasos
• Vértice
• Orientación
• Puntos de corte
• Tabla de valores
– Vamos uno por uno, dibujando a la par la gráfica.

9. EJEMPLO y=x2-4x+3
a=1, b=-4, c=3
VÉRTICE
Tendrás que recordar esta
expresión x=
−𝑏
2𝑎
En este ejemplo:
x=
−(−4)
2·1
= 2
Si x=2  y=22-4·2+3 = -1
El vértice es V(2,-1)

10. EJEMPLO y=x2-4x+3
a=1, b=-4, c=3
ORIENTACIÓN
Para saber hacía dónde mira
la parábola me fijo en ´a´
– a positivo  hacia arriba
– a negativo  hacia abajo
Como a=1 positivo  la
parábola mira hacia arriba

11. EJEMPLO y=x2-4x+3
PUNTOS DE CORTE
Con el eje Y (muy sencillo)
– Haces x=0 y sustituyes:
y=02-4·0+3 = 3 PC(0,3)
Con el eje X
– Haces y=0 y sustituyes
0=x2-4x+3
Ecuación 2º grado  resolver
Solución x=1 
Solución x=3  PC(3,0)

12. EJEMPLO y=x2-4x+3
TABLA DE VALORES
Ya casi está dibujada, calcula
la tabla de valores alrededor
del vértice, que es x=2

13. EJEMPLO y=x2-4x+3
GRÁFICA ACABADA

14. • Dos últimos detalles
1. A veces la ecuación no está completa:
– y=3x2-4x  a=3, b=-4, c=0 y hacerlo igual
– y=5x2 +3  a=5, b=0, c=3 y hacerlo igual
2. En los puntos de corte al resolver la ecuación
de 2º grado, puede tener 2, 1 o 0 soluciones
2 soluciones 1 solución 0 soluciones