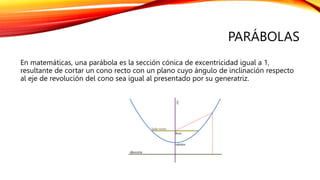
Este documento describe el plano cartesiano o numérico, que consiste en dos rectas perpendiculares (eje x e y) que se cortan en un punto de origen. Explica que este sistema permite describir la posición de puntos y analizar figuras geométricas. También cubre cómo calcular distancias entre puntos y coordenadas de puntos medios, y define ecuaciones, circunferencias, parábolas, hipérbolas y elipses en el plano cartesiano.

1. PLANO NUMÉRICO
Estudiante: Ismael Sandoval
C.I:30454125
Seccion:0404

2. PLANO NUMÉRICO O PLANO
CARTESIANO
Definición
• Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a
dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan
en un punto llamado origen o punto cero.
¿Para que sirve?
La finalidad del plano cartesiano es describir la posición o ubicación de un punto en
el plano, la cual está representada por el sistema de coordenadas.
El plano cartesiano también sirve para analizar matemáticamente figuras geométricas
como la parábola, la hipérbole, la línea, la circunferencia y la elipse, las cuales forman
parte de la geometría analítica.

3. EJEMPLO DE UN PLANO
CARTESIANO

4. DISTANCIA
La distancia del plano cartesiano o numérico radica, en la ubicación de las
coordenadas de dos puntos es posible calcular la distancia entre ellos.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una
recta paralela a este eje, la distancia entre dos puntos corresponde al valor absoluto
de la diferencia de sus abscisas (X2 - x1). Cuando los puntos se encuentran ubicados
sobre el eje y (de las ordenadas) o en una recta paralela a este eje, la distancia entre
los puntos corresponde al valor absoluto de la diferencia de sus ordenadas. (y1 -y2)

5. PUNTO MEDIO DEL PLANO
CARTESIANO
El punto medio, es el punto que se encuentra a la misma distancia de otros dos
puntos cualquiera o extremos de un segmento. Si es un segmento, el punto medio es
el que lo divide en dos partes iguales.
En el plano cartesiano
Dado un segmento, cuyos extremos tienen por coordenadas:
A= (x1 , y1) y B = (x2 , y2)
El punto medio, Pm, tendrá coordenadas:
𝑷𝒎 = (
𝒙𝟏+𝒙𝟐
𝟐
,
𝒚𝟏+𝒚𝟐
𝟐
)

6. ECUACIONES
Una ecuación es una igualdad algebraica en la cual aparecen letras (incógnitas) con
valor desconocido. El grado de una ecuación viene dado por el exponente mayor de
la incógnita. Solucionar una ecuación es determinar el valor o valores de las
incógnitas que transformen la ecuación en una identidad.
Por ejemplo
X + 3 = 11

7. CIRCUNFERENCIA EN EL PLANO
NUMÉRICO
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el
punto ( h, k) distinto del origen y de la radio r consta de todos los puntos ( x, y) que
satisface la ecuación.
(x-h)2 + (y- k)2 = r2 , donde (h, k) es el centro y r es el radio

8. PARÁBOLAS
En matemáticas, una parábola es la sección cónica de excentricidad igual a 1, ​
resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto
al eje de revolución del cono sea igual al presentado por su generatriz.

9. HIPÉRBOLAS
Es una curva abierta de dos ramas, obtenida cortando un cono recto mediante un
plano no necesariamente paralelo al eje de simetría, y con ángulo menor que el de la
generatriz respecto del eje de revolución.

10. ELIPSE
es una curva plana, simple​ y cerrada con dos ejes de simetría que resulta al cortar la
superficie de un cono por un plano oblicuo al eje de simetría con ángulo mayor que
el de la generatriz respecto del eje de revolución.

11. BIBLIOGRAFÍA
• https://www.profesorenlinea.cl
• https://www.significados.com
• www.slideshare.net
• https://es.wikipedia.org