Descargar para leer sin conexión
Subido porDuoc UC
Poliedros
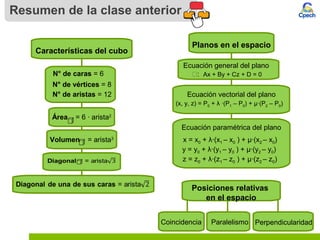
Este documento presenta información sobre poliedros. Define poliedros como cuerpos geométricos delimitados por caras planas. Explica las características del cubo, paralelepípedo, prisma y pirámide, incluyendo sus fórmulas para calcular área y volumen. También incluye ejemplos de cálculos y una pregunta tipo PSU.
Más contenido relacionado
Poliedros
- 1.
- 2. Resumen de laclase anterior Características del cubo Área = 6 · arista2 Volumen = arista3 Posiciones relativas en el espacio Coincidencia PerpendicularidadParalelismo Planos en el espacio Ecuación general del plano �: Ax + By + Cz + D = 0 Ecuación paramétrica del plano Ecuación vectorial del plano (x, y, z) = P0 + λ ·(P1 – P0) + μ·(P2 – P0) x = x0 + λ·(x1 – x0 ) + μ·(x2 – x0) y = y0 + λ·(y1 – y0 ) + μ·(y2 – y0) z = z0 + λ·(z1 – z0 ) + μ·(z2 – z0) N° de caras = 6 N° de vértices = 8 N° de aristas = 12
- 3. Aprendizajes esperados • Clasificarcuerpos geométricos. • Calcular áreas y volúmenes de poliedros.
- 4. Pregunta tipo PSU Elvolumen de un paralelepípedo mide 96 cm3 . Si el ancho y el largo miden 6 y 8 cm, respectivamente, entonces ¿cuánto mide el área de dicho cuerpo? A) 2 cm2 B) 48 cm2 C) 76 cm2 D) 96 cm2 E) 152 cm2
- 5. 1. Cuerpos geométricos 2.Poliedros
- 6. 1. Cuerpos geométricos Definición Loscuerpos geométricos pueden ser de dos clases: o formados por caras planas (poliedros), o teniendo alguna o todas sus caras curvas (cuerpos redondos). Un cuerpo geométrico o sólido es todo lo que ocupa lugar en el espacio. Ejemplos:
- 7. Definición Cada cuerpo geométricoo sólido tiene volumen y área. Volumen: cantidad de espacio que ocupa o que es capaz de contener. Área total: suma de todas las superficies que limitan el cuerpo geométrico. 1. Cuerpos geométricos
- 8. 2. Poliedros Definición Cuerpo tridimensionaldelimitado por caras poligonales planas. vértice arista cara A la línea en la que se intersectan dos caras se le llama arista y al punto en el que concurren tres o más aristas se le llama vértice.
- 9. 2. Poliedros Cubo ohexaedro regular Poliedro formado por 6 caras cuadradas congruentes. Cubo o hexaedro regular 6 8 12 Nº de caras Nº de vértices Nº de aristas Área = 6a2 Volumen = a3 arista (a)
- 10. 2. Poliedros Cubo ohexaedro regular Ejemplo: A = 6∙(3)2 V = 33 3 Determinar el área y volumen de un cubo cuya arista mide 3 cm. A = 54 cm2 V = 27 cm3 A = 6a2 V = a3
- 11. 2. Poliedros Paralelepípedo Poliedro formadopor 6 caras que son paralelogramos. Largo (l) alto (h) ancho (a) Volumen = l ∙ a ∙ h Área = 2(a∙l + a∙h + l∙h) Las tres parejas de caras opuestas son paralelas y congruentes entre sí.
- 12. 2. Poliedros Paralelepípedo Ejemplo: Determinar elvolumen de una piscina cuyo largo, ancho y alto miden 3, 2 y 2,5 metros respectivamente. Solución: Volumen = l ∙ a ∙ h Volumen = 3 ∙ 2 ∙ 2,5 Volumen = 15 m3
- 13. Calcular el áreay el volumen de una caja de zapatos de 20 cm de ancho, 30 cm de largo, y 10 cm de alto. Ejemplo: Para el área se tiene: Área = 2(largo ⋅ ancho + largo ⋅ alto + ancho ⋅ alto) Área = 2(30 ⋅ 20 + 30 ⋅ 10 + 20 ⋅ 10) Área = 2(600 + 300 + 200) Área = 2 · (1.100) Área = 2.200 cm2 Para el volumen se tiene: Volumen = largo ⋅ ancho ⋅ alto Volumen = 30 ⋅ 20 ⋅ 10 Volumen = 6.000 cm3 2. Poliedros Paralelepípedo
- 14. 2. Poliedros Prismas Sólido compuestopor dos polígonos paralelos y congruentes llamados bases y paralelógramos que unen las bases denominadas caras. Volumen = Área basal · altura Área = 2 · Área basal + Área caras (área lateral) Prisma triangular Prisma cuadrangular Prisma pentagonal Prisma hexagonal
- 15. Calcula el áreay volumen de un prisma de 10 cm de altura y cuya base es un rombo de diagonales 6 y 8 cm. Ejemplo: Volumen = Área basal · altura Volumen = 24⋅ 10 Volumen = 240 cm3 2. Poliedros Prismas Área = 2 · Área basal + Área caras (área lateral) Área = 2 · 24 + 4 ⋅ 50 = 48 + 200 = 248 cm2 Área = 2 · + 4 · (5 · 10) 2 86⋅
- 16. 2. Poliedros Pirámides Sólido compuestopor un polígono llamado base y caras triangulares que coinciden en un vértice. Volumen = · área basal · altura Área = Área basal + Área caras (área lateral) 3 1 Pirámide triangular Pirámide cuadrangular Pirámide pentagonal Pirámide hexagonal
- 17. Ejemplo: 2. Poliedros Pirámides Área =Área basal + Área caras (área lateral) Área = 100 + 260 = 360 cm2 Área = 10 · 10 + 4 · ⋅ 2 1310 Volumen = · área basal · altura Volumen = · 100 · 12 Volumen = 400 cm3 3 1 3 1
- 18. Pregunta tipo PSU ALTERNATIVA CORRECTA E Elvolumen de un paralelepípedo mide 96 cm3 . Si el ancho y el largo miden 6 y 8 cm, respectivamente, entonces ¿cuánto mide el área de dicho cuerpo? A) 2 cm2 B) 48 cm2 C) 76 cm2 D) 96 cm2 E) 152 cm2
- 19. Tabla de corrección NºClave Unidad temática Habilidad 1 D Cuerpos geométricos Aplicación 2 A Cuerpos geométricos Comprensión 3 E Cuerpos geométricos Aplicación 4 B Cuerpos geométricos ASE 5 D Cuerpos geométricos ASE 6 C Cuerpos geométricos Aplicación 7 D Cuerpos geométricos Aplicación 8 B Cuerpos geométricos Aplicación 9 D Cuerpos geométricos ASE 10 C Cuerpos geométricos Aplicación 11 E Cuerpos geométricos ASE 12 D Cuerpos geométricos ASE
- 20. Tabla de corrección NºClave Unidad temática Habilidad 13 A Cuerpos geométricos Aplicación 14 C Cuerpos geométricos Aplicación 15 E Cuerpos geométricos Comprensión 16 B Cuerpos geométricos Comprensión 17 C Cuerpos geométricos Aplicación 18 D Cuerpos geométricos Aplicación 19 B Cuerpos geométricos ASE 20 B Cuerpos geométricos Aplicación 21 A Cuerpos geométricos Comprensión 22 D Cuerpos geométricos Aplicación 23 D Cuerpos geométricos ASE 24 A Cuerpos geométricos ASE 25 D Cuerpos geométricos ASE
- 21. Síntesis de laclase Cuerpos geométricos Poliedros Cubo a Á = 6a2 Vol = a3 Paralelepípedo h l a Vol = l · a · h Á = 2(a·l + a·h + l·h) Prisma Á = 2 · Á basal + Á caras Vol = Á basal · altura Pirámide Á = Á basal + Á caras Vol = ·Á basal · altura 3 1
- 22. Prepara tu próximaclase En la próxima sesión, estudiaremos Cuerpos redondos
- 24. Propiedad Intelectual CpechRDA: 186414 ESTE MATERIAL SE ENCUENTRA PROTEGIDO POR EL REGISTRO DE PROPIEDAD INTELECTUAL. Equipo Editorial Matemática