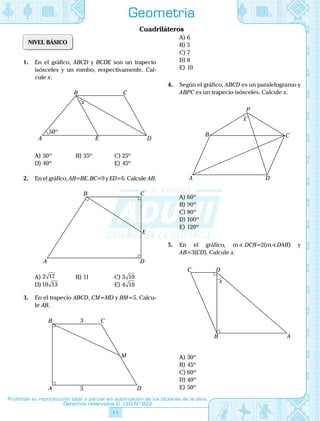
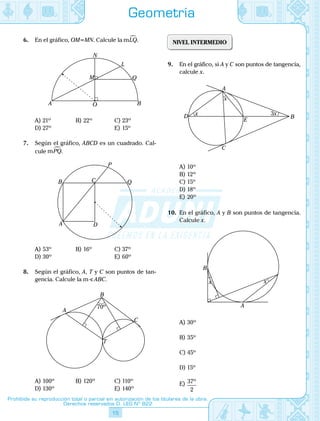
El documento presenta 15 problemas de geometría sobre triángulos, congruencia de triángulos y aplicaciones de la congruencia. Los problemas están organizados en 3 niveles de dificultad (básico, intermedio y avanzado) y cubren temas como ángulos, lados, alturas, bisectrices y mediatrices.

2. 2
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
Triángulos I
NIVEL BÁSICO
1. Según el gráfico, calcule x+y si a – b=55º.
α
β θ
θ
x
y
A) 55º B) 110º C) 125º
D) 120º E) 135º
2. A partir del gráfico, halle x+y+z.
α
α θ
θ
x
z
y
A) 180º
B) 120º
C) 135º
D) 150º
E) 200º
3. En el gráfico, y+z=100º. Calcule q – w.
θ
zy
ω
20º
40º
A) 150º
B) 140º
C) 130º
D) 120º
E) 160º
4. En el gráfico, halle x – y.
θ
θ
x
y
150º
A) 30º
B) 75º
C) 50º
D) 60º
E) 40º
5. Según el gráfico, calcule x+y.
β
β
β
β
β
x
y
A) 120º
B) 144º
C) 150º
D) 100º
E) 135º

3. 3
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
6. En el gráfico, m+n=110º. Calcule x.
β2β θ 2θ
40º
x
m
n
A) 110º B) 105º C) 50º
D) 50º E) 55º
7. En el gráfico, a+b+c+d=160º. Calcule x+y.
d
cn
n
x
y
b
a
A) 200º B) 110º C) 80º
D) 160º E) 100º
8. En el gráfico, a+b+c+d=230º. Calcule x+y.
cb
a d
n y
x
n
A) 100º B) 120º C) 125º
D) 130º E) 150º
NIVEL INTERMEDIO
9. En el gráfico mostrado, calcule x – y.
θ θ
53ºxy85º
A) 16º
B) 30º
C) 37º
D) 45º
E) 32º
10. Según el gráfico, m+n=120º. Calcule x.
120º
2x
m
n
x
A) 20º B) 30º C) 40º
D) 50º E) 15º
11. En el gráfico, halle a.
40º
50º
α
α
ββ
θ
θ
A) 10º B) 20º C) 25º
D) 30º E) 15º

4. 4
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
12. Según el gráfico, calcule x si m+n=200º.
80º
β βθ
θ
x
n
m
A) 100º B) 120º C) 110º
D) 150º E) 160º
NIVEL AVANZADO
13. Del gráfico, calcule x.
2ββ
β
θ
θ2α
α+β
x
A) 105ºº
B) 115º
C) 90º
D) 120º
E) 110º
14. En el gráfico, calcule x.
α
α β
β
ω2ωθ
2θ
60º
x
A) 45º
B) 60º
C) 30º
D) 90º
E) 75º
15. Según el gráfico, calcule x.
α
7α
β7β
θ
8θ
x
8φ
φ
A) 140º
B) 110º
C) 100º
D) 160º
E) 120º

5. 5
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
Triángulos II
NIVEL BÁSICO
1. Según el gráfico, BH es la altura y BC=6.
Calcule AC.
H
B
20º
40º
CA
A) 4 B) 6 C) 8
D) 10 E) 7
2. Según el gráfico, BD es bisectriz exterior del
triángulo ABC y AB=BD. Calcule x.
C
B
DA
x
2x
A) 10º B) 20º C) 12º
D) 15º E) 18º
3. En un triángulo rectángulo ABC, recto en B, se
trazan la altura BH y la bisectriz BN del ángulo
ABH (N ∈ AH). Calcule BC si NC=5.
A) 6 B) 5 C) 4
D) 3 E) 7
4. En un triángulo ABC se traza la bisectriz inte-
rior BD, tal que m DBC=40º, m ACB=30º y
AB=6. Calcule BD.
A) 8 B) 10 C) 7
D) 5 E) 6
5. Según el gráfico, calcule x, si w+a=67,5º
x
α
α
θ
θ
β
β
ω
ω
A) 40º
B) 44º
C) 46º
D) 45º
E) 50º
6. En el gráfico, BM es mediana. Calcule x.
(BM=MC)
A M C
B
5x x
A) 10º
B) 17º
C) 15º
D) 12º
E) 9º
7. En la región exterior relativa al lado AC de un
triángulo ABC, se ubica el punto D, tal que
m BDA=2m (BCA)=20º, AC=AD y BC=CD.
Calcule m CDA.
A) 40º
B) 35º
C) 55º
D) 45º
E) 70º

6. 6
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
8. Según el gráfico, calcule a si AB=BC y
AC=CE=ED.
3α
α
B
C
E
A D
A) 18º B) 20º C) 21º
D) 15º E) 16º
NIVEL INTERMEDIO
9. En el gráfico, AB=BC y CD=DE. Calcule x.
A C E
D
B
50º 40º
x
θ θ
β
β
A) 80º B) 100º C) 120º
D) 140º E) 160º
10. En un triángulo rectángulo ABC, recto en B
(BC > AB), se traza la bisectriz interior BF y
la ceviana BM. Si AB=BF y BM=MC, calcule
m FBM.
A) 22º30’ B) 45º C) 30º
D) 20º E) 25º
11. En un triángulo ABC se traza la bisectriz in-
terior BP. Luego, en el triángulo ABP, se
traza la altura AQ. Calcule la m BCA si
m BAQ – m PAQ=34º.
A) 17º
B) 24º
C) 46º
D) 34º
E) 68º
12. Según el gráfico, a+q=260º. Calcule x+y.
b
a
x y
a
b
θ
α
A) 250º
B) 260º
C) 200º
D) 215º
E) 220º
NIVEL AVANZADO
13. En el triángulo ABC se trazan las alturas AP y
BQ, tal que m ABQ=10º. Calcule la medida
del ángulo determinado por las bisectrices de
los ángulos BAP y BCA.
A) 75º
B) 85º
C) 65º
D) 50º
E) 95º

7. 7
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
14. Del gráfico, calcule x.
α α
β β
ω
ω
θ θ
x
80º80º
A) 90º
B) 100º
C) 110º
D) 120º
E) 130º
15. Según el gráfico, AC=CD=BD. Calcule x.
x
D
C
A
B
120º
θ
θ
A) 20º
B) 15º
C) 25º
D) 30º
E) 35º

8. 8
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
Congruencia de triángulos
y Aplicaciones de la congruencia
NIVEL BÁSICO
1. Si AP=5, halle HB.
37º
45º
PA C
H
B
A) 18 B) 21 C) 24
D) 23 E) 19
2. En el gráfico, si AM=MC=5, AF=1 y FB=7, cal-
cule x.
BF
x
A
M
C
A) 60º B) 37º C) 30º
D) 45º E) 53º
3. Según el gráfico, halle x si BC=4(AB)=4(CD).
B C DA
x x
x
A) 30º
B) 37º
C) 45º
D) 53º
E) 60º
4. En el gráfico, BM es mediana, AB=8 y BC=5.
Calcule x.
B
53º
M CA
x
A) 16º B) 30º C) 45º
D) 60º E) 37º
5. Según el gráfico, AF=FB=5, m FAC=90º y
BC=6. Calcule m BCA.
θ
2θ
A
F
B C
A) 30º
B) 37º
C)
53
2
º
D)
45
2
º
E)
37
2
º

9. 9
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
6. En el gráfico, BM=MC, AB=8 y FC=5. Calcule AF.
F
M
B
60º
CA
120º
A) 16 B) 12 C) 15
D) 13 E) 14
7. En el gráfico, BC=CQ, AB=5 y BQ=8. Calcule q.
CA
B
Q
θ
θ
A) 30º B) 37º C) 26,5º
D) 22,5º E) 53º
8. Si L 1 y L 2 son mediatrices de AB y CD, respec-
tivamente, además AF=BC=FD y q+b=50º,
calcule x.
A
B
C
DF
θ
β
L 2
L 1
x
A) 130º B) 140º C) 110º
D) 90º E) 100º
NIVEL INTERMEDIO
9. Si AB+AC=18, calcule MF.
45º
A
B
M
F
C
A) 3 2 B) 3 6 C) 6
D) 9 E) 12
10. Se tiene un triángulo rectángulo APD recto en
P, donde C es punto medio de AD, y en la pro-
longación de AP se ubica el punto B, tal que
AB=BC y AD=2(BP). Calcule la m ADP.
A) 15º
B) 18º
C) 22,5º
D) 18,5º
E) 30º
11. Si AB=BC=2(AF)=6 y AC=8, calcule MF.
A
F
M
B
C
θ
4θ
A) 5
B) 7
C) 5 2
D) 4 6
E) 26

10. 10
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
12. En el gráfico, PB=BQ y HA=HQ+HC. Calcule x.
A
P
Q
B
CH
θ θx 50º
A) 50º B) 40º C) 25º
D) 30º E) 60º
NIVEL AVANZADO
13. En un triángulo rectángulo ABC recto en B,
la mediatriz de la bisectriz interior AE inter-
seca a la prolongación de CB en D. Calcule la
m ACB si DE=AC.
A) 30º B) 45º C) 37º
D) 53º E) 60º
14. Se tiene un triángulo ABC. En AB y AC se ubi-
can los puntos M y F, tal que AM=FC y MF=FB.
Calcule la m FBC si m AMF=m BFC y
m BAC=30º.
A) 30º
B) 37º
C) 53º
D) 45º
E)
53
2
º
15. Se tiene un triángulo ABC, en el cual se traza
la mediana BM y la ceviana AQ, las cuales se
intersecan en P y m BPA=90º. Si BC=2(AP),
calcule la m BQA.
A) 30º
B) 37º
C) 45º
D) 53º
E) 60º

11. 11
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
Cuadriláteros
NIVEL BÁSICO
1. En el gráfico, ABCD y BCDE son un trapecio
isósceles y un rombo, respectivamente. Cal-
cule x.
B C
E
50º
x
DA
A) 30º B) 35º C) 25º
D) 40º E) 45º
2. En el gráfico, AB=BE, BC=9 y ED=6. Calcule AB.
A D
CB
E
A) 2 17 B) 11 C) 3 10
D) 10 13 E) 4 10
3. En el trapecio ABCD, CM=MD y BM=5. Calcu-
le AB.
A 5
3
D
CB
M
A) 6
B) 5
C) 7
D) 8
E) 10
4. Según el gráfico, ABCD es un paralelogramo y
ABPC es un trapecio isósceles. Calcule x.
A D
CB
P
x
A) 60º
B) 90º
C) 80º
D) 100º
E) 120º
5. En el gráfico, m DCB=2(m DAB) y
AB=3(CD). Calcule x.
B A
DC
x
A) 30º
B) 45º
C) 60º
D) 40º
E) 50º

12. 12
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
6. En el gráfico, FD = 2 5. Calcule CD.
C
D
F
45º
A) 2 B) 4 C) 6
D) 3 2 E) 2 2
7. En un romboide ABCD se ubica el punto P
en la región interior, tal que m BCD=53º,
mS PDC=90º, PD=DC y BC=2(AB)=10. Calcu-
le la mS BAP.
A)
53
2
º
B)
37
2
º
C) 45º
D) 37º E) 16º
8. Dado un trapecio ABCD (BC // AD), en la pro-
longación de DC se ubica el punto P, tal que
m ADC=m MPD (M es punto medio de AB).
Si BC=10 y AD=26, calcule PM.
A) 10 B) 26 C) 15
D) 18 E) 12
NIVEL INTERMEDIO
9. En un cuadrilátero ABCD recto en A y C, AB=6,
AD=10 y BC=CD. Halle la distancia de C a AD.
A) 6 B) 7 C) 8
D) 9 E) 10
10. En un rombo ABCD, en BC y en la prolonga-
ción de AB se ubican los puntos P y Q, respec-
tivamente. Si PQ AB⊥ , m PAD=3(m PAB) y
2(PQ)=PC, calcule m PAB.
A) 30º B) 15º C) 20º
D) 10º E) 5º
11. Se tiene un trapecio isósceles, tal que sus dia-
gonales son perpendiculares a sus lados late-
rales y miden 80. Si la base mayor mide 100,
halle la longitud de la base menor.
A) 30 B) 34 C) 36
D) 26 E) 28
12. En el gráfico, ABCD es un romboide. Si PQ=32,
calcule AE.
A D
C
P
B
Q
E
40º
20º
A) 6 B) 8 C) 10
D) 12 E) 16
NIVEL AVANZADO
13. En el gráfico, m BCA – m APQ=60º, y
AB=BQ. Calcule la m BPA.
θ
60º–θ
A
B
Q
P
C
x
A) 40º B) 30º C) 35º
D) 20º E) 25º

13. 13
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
14. Dado un cuadrado ABCD, en AD y en su pro-
longación se ubican los puntos M y N, respec-
tivamente, tal que m DCN=2(m ACM) y
MN AB= ( )2 . Calcule la m CMN.
A) 22º 30'
B) 60º
C) 75º
D) 67º 30'
E) 53º
15. En un trapecio ABCD (BC // AD) se trazan las
bisectrices interiores de los ángulos ABC y
BAD, que se intersecan en el punto P, y lue-
go se traza PM // BC (M ∈ CD). Si AB=a, BC=b y
AD=c, calcule PM.
A)
b c a+ +
2
B)
2
2
b c a+ −
C)
a b c+ −
2
D)
a c b+ −
2
E)
b c a+ −
2

14. 14
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
Circunferencia
NIVEL BÁSICO
1. En el gráfico, ABCD es un rombo. Calcule la
mPQ.
A
70º B
C
Q
D
P
A) 30º B) 40º C) 50º
D) 60º E) 70º
2. En el gráfico se cumple que O es centro y
CD // AB. Calcule x.
A
D C
7x
x
O B
A) 20º B) 18º C) 12º
D) 15º E) 22º
3. En el gráfico, el triángulo ABC es equilátero. Si
m =mARB QP y m =mDBR DR, calcule
BR
CR
.
AQ
P
C
R
B
D
A)
3
3
B) 2
C)
6
2
D) 3
E)
3
2
4. Del gráfico, calcule mABC.
A
C
B
20º
60º60º
A) 100º B) 160º C) 140º
D) 110º E) 150º
5. En el gráfico, mAQE mBPT + = 190º y
mED = 130º. Calcule mTC.
A
Q E
D
B
P
T
C
A) 70º
B) 50º
C) 40º
D) 80º
E) 90º

15. 15
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
6. En el gráfico, OM=MN. Calcule la mLQ.
A BO
M
N
Q
L
A) 21º B) 22º C) 23º
D) 27º E) 15º
7. Según el gráfico, ABCD es un cuadrado. Cal-
cule mPQ.
A
B C
P
Q
D
A) 53º B) 16º C) 37º
D) 30º E) 60º
8. Según el gráfico, A, T y C son puntos de tan-
gencia. Calcule la mS ABC.
C
T
B
A
70º
A) 100º B) 120º C) 110º
D) 130º E) 140º
NIVEL INTERMEDIO
9. En el gráfico, si A y C son puntos de tangencia,
calcule x.
A
D
E
B
C
x
3xx
A) 10º
B) 12º
C) 15º
D) 18º
E) 20º
10. En el gráfico, A y B son puntos de tangencia.
Calcule x.
B
x
A
xx
A) 30º
B) 35º
C) 45º
D) 15º
E) 37
2
º

16. 16
Prohibida su reproducción total o parcial sin autorización de los titulares de la obra.
Derechos reservados D. LEG Nº 822
Geometría
11. En el gráfico, AM=MC y OB=BD. Calcule mAE.
A
E
M
C
B DO
A) 23º B) 16º C) 18º
D) 65º E) 24º
12. En el gráfico, ABCD es un cuadrado. Calcule la
mNC. (M es punto de tangencia).
CNB
M
A D
A) 37º B) 74º C) 53º
D) 106º E) 65º
NIVEL AVANZADO
13. En el gráfico, m mABC TFE= = 2θ, TF=EF
(T es punto de tangencia). Calcule mBC en
términos de q.
A
B
C
E
T
F
A) q
B) 90º – q
C)
3
2
q
D) 120º – q
E) 120 – 2q
14. Según el gráfico, calcule la mBC si ABCD es
un cuadrado.
A
B
C
D
A) 37º
B) 40º
C) 45º
D) 60º
E) 65º
15. Del gráfico, calcule R si OC=2 y OB=6.
A
R
BOC
A) 1
B) 2
C) 2 5
D) 3
E) 3 5

17. Semestral San Marcos
Triángulos I
01 - c
02 - A
03 - E
04 - A
05 - b
06 - b
07 - D
08 - D
09 - e
10 - A
11 - D
12 - C
13 - C
14 - B
15 - A
01 - c
02 - A
03 - E
04 - A
05 - b
06 - b
07 - D
08 - D
09 - e
10 - A
11 - D
12 - C
13 - C
14 - B
15 - A
Congruencias de triángulos y Aplicaciones de la congruencia
01 - B
02 - D
03 - D
04 - b
05 - b
06 - D
07 - E
08 - C
09 - D
10 - B
11 - A
12 - C
13 - B
14 - D
15 - E
01 - B
02 - D
03 - D
04 - b
05 - b
06 - D
07 - E
08 - C
09 - D
10 - B
11 - A
12 - C
13 - B
14 - D
15 - E
Triángulos II
01 - B
02 - B
03 - B
04 - E
05 - D
06 - C
07 - E
08 - a
09 - C
10 - A
11 - D
12 - E
13 - E
14 - C
15 - D
01 - B
02 - B
03 - B
04 - E
05 - D
06 - C
07 - E
08 - a
09 - C
10 - A
11 - D
12 - E
13 - E
14 - C
15 - D
Cuadriláteros
01 - c
02 - C
03 - A
04 - b
05 - C
06 - D
07 - A
08 - D
09 - C
10 - B
11 - E
12 - B
13 - B
14 - a
15 - E
01 - c
02 - C
03 - A
04 - b
05 - C
06 - D
07 - A
08 - D
09 - C
10 - B
11 - E
12 - B
13 - B
14 - a
15 - E
Circunferencia
01 - B
02 - D
03 - D
04 - b
05 - C
06 - C
07 - c
08 - E
09 - D
10 - D
11 - B
12 - B
13 - A
14 - a
15 - c
01 - B
02 - D
03 - D
04 - b
05 - C
06 - C
07 - c
08 - E
09 - D
10 - D
11 - B
12 - B
13 - A
14 - a
15 - c