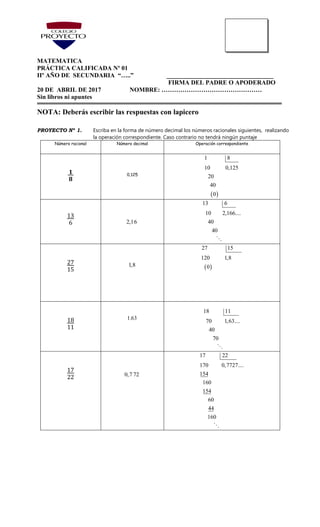
1) El documento presenta 19 proyectos de matemáticas sobre números racionales e irracionales, operaciones con fracciones y conjuntos numéricos. 2) Los proyectos incluyen convertir números entre formas decimal y fraccional, calcular fracciones generatrizas, determinar si afirmaciones son verdaderas o falsas, y realizar operaciones con conjuntos. 3) El documento proporciona problemas y sus soluciones de manera secuencial.

1. MATEMATICA
PRÁCTICA CALIFICADA Nº 01
IIº AÑO DE SECUNDARIA “…..” __________________________________
FIRMA DEL PADRE O APODERADO
20 DE ABRIL DE 2017 NOMBRE: …………………………………………
Sin libros ni apuntes
NOTA: Deberás escribir las respuestas con lapicero
PROYECTO Nº 1. Escriba en la forma de número decimal los números racionales siguientes, realizando
la operación correspondiente. Caso contrario no tendrá ningún puntaje
Número racional Número decimal Operación correspondiente
𝟏
𝟖
0,125
 
1 8
10 0,125
20
40
0
13
6 2,16
13 6
10 2,166....
40
40
27
15
1,8  
27 15
120 1,8
0
18
11
1.63
18 11
70 1,63....
40
70
17
22 0,7 72
17 22
170 0,7727....
154
160
154
60
44
160

2. 23
35 0,6571428
230 35
210 0,65714285....
200
175
250
245
50
35
150
140
100
70
300
280
200
PROYECTO Nº 2. Escriba en la forma de número racional, los siguientes números decimales, realizando la
operación correspondiente. Caso contrario no tendrá ningún puntaje
Número racional Número decimal Operación correspondiente
211
900
0, 234444444……….
234 23 211
900 900


161
80
2,0125 20125 161
10000 80

134
55
2,436363636…….. 2436 24 2412 134
990 990 55

 
169
165
1,02424242……. 1024 10 1014 169
990 990 165

 
9 8,999999…….. 89 8 81
9
9 9

 

3. 7397
3300
2,2415151515……. 22415 224 22191 7397
9900 9900 3300

 
171717
1000000
0,171717 171717
0,171717
1000000

1234567
10000000
0,1234567 1234567
0,1234567
10000000

PROYECTO Nº 3. La generatriz de 3,066666…. es:
Solución
306 30 276 46 1
3,0666... 9
900 30 5 5

   
PROYECTO Nº 4. El decimal periódico 2,04373737 ….. equivalente a la fracción
Solución
20437 204 20233 20233
2,04373737...
9900 9900 9900

  
PROYECTO Nº 5. Determine la fracción generatriz de 0,277777….
Solución
27 2 25 5
0,2777...
90 90 18

  
PROYECTO Nº 6. Luego de obtener la fracción generatriz irreductible del número decimal: 4,1212 se
nota que el numerador excede al denominador en:
Solución
41212 10303
4,1212
10000 2500
 
Luego, 10 303 – 2 500 = 7 803
PROYECTO Nº 7. Al calcular la fracción generatriz del número decimal: 0,76666…… se observa que el
denominador excede al numerador en:
Solución
76 7 69 23
0,7666...
90 90 30

  
Luego, el denominador excede al numerador en 30 – 23 = 7
PROYECTO Nº 8. Dado el conjunto: 33
;0,9; ; 225; 36; 8;0
5


 
   
 
. ¿Cuántos de sus elementos
son números irracionales?
Solución
Sólo 1, el número 

4. PROYECTO Nº 9. Señalar si la afirmación es correcta (V) o falsa (F):
I. Todo número irracional se puede expresar como a/b . (F)
II. 0,56789999 es número irracional (F)
III. 0,767777.. < 0,78777 (V)
PROYECTO Nº 10. La división de las fracciones generatrices de los números decimales periódicos
2,1363636… y 1,454545…. respectivamente, es igual a:
Solución
2136 21
2.1363636... 9900
145 11.454545...
990
2115
990
144
99
47
22
16
11
47 11
22 16
47
32
15
1
32










PROYECTO Nº 11. ¿Cuánto le falta a 0,263636363… para ser igual a los 2/3 de los 5/7 de 6/11 de 7
Solución
2 5 6 263 2
7
3 7 11 990
20 261
11 990
20 29
11 110
200 29
110
171
110
61
1
110

   
 
 




PROYECTO Nº 12. Calcular: (I - Q)  (R – Q), Sabiendo que:
I: Conjunto de los números irracionales
Q: Conjunto de los números racionales
R: Conjunto de los números reales
Solución
     
     
 


5. PROYECTO Nº 13. Al efectuar:
2
0,89999...
9
 el resultado tiene un período de:
Solución
2 89 8 2
0,8999...
9 90 9
81 2
90 9
81 20
90 90
101
90
1.1222....
1.12

  
 
 



El período es 2 ó tiene un período de una cifra.
PROYECTO Nº 14. ¿Cuál es el número real que antecede a 1,5?
Solución
No se puede determinar
PROYECTO Nº 15. El número real que le sigue a 4,8 es:
Solución
No se puede determinar
PROYECTO Nº 16. Luego de obtener la fracción generatriz del número decimal: 0,1545454….; dar como
respuesta la diferencia de sus términos.
Solución
154 1 153 17
0,154545454...
990 990 110

  
Luego, 110 – 17 = 93
PROYECTO Nº 17. Al calcular la fracción generatriz del número decimal: 0,1535353…se observa que el
denominador excede al numerador en:
Solución
153 1 152 76
0,1535353...
990 990 495

  
Luego, el denominador excede al numerador en 495 – 76 = 419
PROYECTO Nº 18. ¿Cuántos de los siguientes enunciados son falsos?
a) (– 6)2
es número natural (V)
b) – 0.01234567…. es número real (V)
c) 2.456789 es número racional (V)
d) (-64)1/2
es irracional (F)
e) 2 : 1,414213….. tiene como resultado un racional (F)
Solución
2 enunciados falsos
PROYECTO Nº 19. Respecto a los conjuntos numéricos, indicar verdadero (V) o falso (F):
Solución
i) N  Q (V)
ii) R  I (F)
iii) Q  Z (F)
iv) N  R (V)