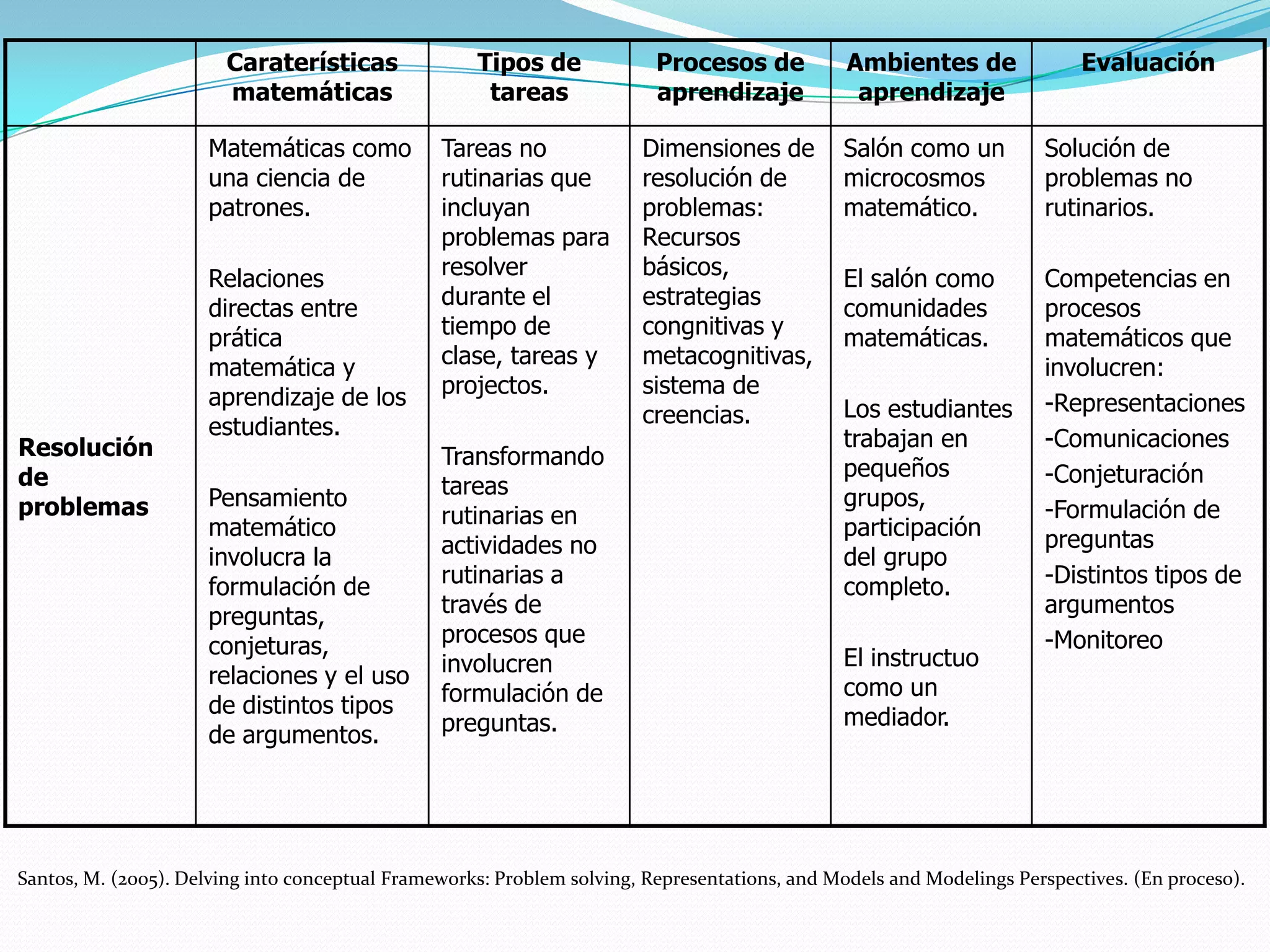
El documento describe la evolución histórica de la educación matemática y la resolución de problemas desde la década de 1950 hasta la actualidad. Explica diferentes interpretaciones de la resolución de problemas, incluyendo como contexto, habilidad y arte. También describe características de problemas rutinarios y no rutinarios, dimensiones que influyen en la resolución de problemas, y objetivos de la instrucción bajo la perspectiva de resolución de problemas. Principales exponentes discutidos incluyen a Polya, Schoenfeld y Santos Trigo.