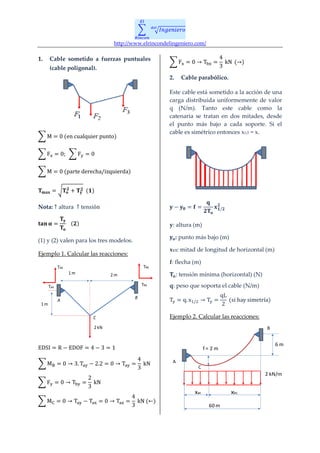
El documento aborda el análisis de cables sometidos a diferentes fuerzas: cables poligonales, parabólicos y catenarios. Se presentan fórmulas específicas para calcular tensiones, reacciones y longitudes en diversos ejemplos prácticos. Asimismo, se detallan las condiciones de simetría y el efecto de cargas distribuidas en la tensión de los cables.

1. ෍ ඥ‫݋ݎ݁݅݊݁݃݊ܫ‬೏೐೗
ா௟
ோ௜௡௖௢௡
http://www.elrincondelingeniero.com/
1. Cable sometido a fuerzas puntuales
(cable poligonal).
෍ M ൌ 0 ሺen cualquier puntoሻ
෍ F୶ ൌ 0; ෍ F୷ ൌ 0
෍ M ൌ 0 ሺparte derecha/izquierdaሻ
‫܂‬‫ܠ܉ܕ‬ ൌ ට‫܂‬‫ܗ‬
૛ ൅ ‫܂‬‫ܡ‬
૛ ሺ૚ሻ
Nota: ՛ altura ՛ tensión
‫ܖ܉ܜ‬ હ ൌ
‫܂‬‫ܡ‬
‫܂‬‫ܗ‬
ሺ૛ሻ
(1) y (2) valen para los tres modelos.
Ejemplo 1. Calcular las reacciones:
EDSI ൌ R െ EDOF ൌ 4 െ 3 ൌ 1
෍ M୆ ൌ 0 ՜ 3. Tୟ୷ െ 2.2 ൌ 0 ՜ Tୟ୷ ൌ
4
3
kN
෍ F୷ ൌ 0 ՜ Tୠ୷ ൌ
2
3
kN
෍ Mେ ൌ 0 ՜ Tୟ୷ െ Tୟ୶ ൌ 0 ՜ Tୟ୶ ൌ
4
3
kN ሺ՚ሻ
෍ F୶ ൌ 0 ՜ Tୠ୶ ൌ
4
3
kN ሺ՜ሻ
2. Cable parabólico.
Este cable está sometido a la acción de una
carga distribuida uniformemente de valor
q (N/m). Tanto este cable como la
catenaria se tratan en dos mitades, desde
el punto más bajo a cada soporte. Si el
cable es simétrico entonces x1/2 = x.
‫ܡ‬ െ ‫ܡ‬૙ ൌ ܎ ൌ
‫ܙ‬
૛‫܂‬‫ܗ‬
‫ܠ‬૚/૛
૛
y: altura (m)
‫ܡ‬‫ܗ‬: punto más bajo (m)
x1/2: mitad de longitud de horizontal (m)
f: flecha (m)
‫܂‬‫ܗ‬: tensión mínima (horizontal) (N)
q: peso que soporta el cable (N/m)
T୷ ൌ q. xଵ/ଶ ՜ T୷ ൌ
qL
2
ሺsi hay simetríaሻ
Ejemplo 2. Calcular las reacciones:
A
B
C
1 m
1 m 2 m
2 kN
Tay
Tax
Tbx
Tby
2 kN/m
6 m
f = 2 m
60 m
A
C
B
xac xbc

2. ෍ ඥ‫݋ݎ݁݅݊݁݃݊ܫ‬೏೐೗
ா௟
ோ௜௡௖௢௡
http://www.elrincondelingeniero.com/
y െ y଴ ൌ 2 ൌ
2
2T୭
xୟୡ
ଶ
ሺ૜ሻ
y െ y୭ ൌ 8 ൌ
2
2T୭
xୠୡ
ଶ
ሺ૝ሻ
4 ൌ
xୠୡ
ଶ
xୟୡ
ଶ ՜ xୠୡ ൌ 2xୟୡ ሺcombinando 3 y 4ሻ
xୟୡ ൅ xୠୡ ൌ 60 ՜ xୟୡ ൌ 20 m ՜ xୠୡ ൌ 40 m
T୭ ൌ
xୟୡ
ଶ
2
ൌ 200 kN
Tୟ୷ ൌ q. xୟୡ ൌ 2.20 ൌ 40 kN
Tୠ୷ ൌ q. xୠୡ ൌ 2.40 ൌ 80 kN
‫܂‬‫܉‬ ൌ ൫‫܂‬‫ܗ‬, ‫܂‬‫ܡ܉‬൯ ൌ ሺെ૛૙૙, ૝૙ሻ ‫ۼܓ‬
‫܂‬‫܊‬ ൌ ൫‫܂‬‫ܗ‬, ‫܂‬‫ܡ܊‬൯ ൌ ሺ૛૙૙, ૡ૙ሻ ‫ۼܓ‬
3. Catenaria.
La catenaria es un cable que simplemente
está sujeto a la acción de su propio peso, y
que podemos ver en infinidad de
ocasiones en la naturaleza (por ej. en una
tela de araña o en una cadena apoyada en
dos puntos).
‫܉‬ ൌ
‫܂‬‫ܗ‬
‫ܘ‬
ൌ parámetro de la catenaria ሺmሻ
‫܂‬‫ܗ‬: tensión mínima (horizontal) (N)
p: peso por unidad de longitud (N/m)
‫ܡ‬ ൌ ‫܉‬ ‫ܐܛܗ܋‬ቀ
‫ܠ‬૚/૛
‫܉‬
ቁ ՜ altura ሺmሻ ; ሺ૞ሻ
‫ܛ‬૚/૛ ൌ ‫܉‬ ‫ܐܖܑܛ‬ቀ
‫ܠ‬૚/૛
‫܉‬
ቁ ՜ ሺmሻ; ሺ૟ሻ
s1/2: semi-longitud del cable: s୘ ൌ 2sଵ/ଶ
‫ܛ‬૚/૛
૛
ൌ ‫ܡ‬૛
െ ‫܉‬૛
՜ utilizando ሺ5ሻ y ሺ6ሻ
T୷ ൌ p. sଵ/ଶ ሺen cada apoyo por simetríaሻ
‫܂‬ ൌ ‫.ܘ‬ ‫ܡ‬ ՜ T: tensión vectorial (N)
‫܂‬ ൌ ට‫܂‬‫ܗ‬
૛ ൅ ‫܂‬‫ܡ‬
૛
dsଶ
ൌ dxଶ
൅ dyଶ
՜ ൬
ds
dx
൰
ଶ
ൌ 1 ൅ ൬
dy
dx
൰
ଶ
ds ൌ ඥ1 ൅ yԢଶ. dx ՜ ‫ܛ‬ ൌ න ඥ૚ ൅ ‫ܡ‬Ԣ૛
‫܊‬
‫܉‬
. ‫ܠ܌‬
Nota: ecuación solo a emplear si se conoce
y(x). Es una expresión poco empleada en este
tipo de problemas.
Ejercicio 3: Calcular la reacción en los apoyos
y la longitud del cable:
a ൌ
T୭
p
՜ ‫܂‬‫ܗ‬ ൌ a. p ൌ 5 kN
y ൌ a cosh ቀ
xଵ/ଶ
a
ቁ ൌ 10 cosh ൬
15
10
൰ ൌ 23,52 m
T ൌ py ൌ 11,76 kN
‫܂‬‫ܡ܉‬ ൌ ‫܂‬‫ܡ܊‬ ൌ ටTଶ െ T୭
ଶ ൌ 10,64 kN
Calculo de la longitud:
sଵ/ଶ ൌ ඥyଶ െ aଶ ൌ 21,29 m
sଵ/ଶ ൌ 10 sinh ൬
15
10
൰ ൌ 21,29 m ሺveriϐicaciónሻ
s୘ ൌ 2. sଵ/ଶ ൌ 42,58 m ሺlongitud totalሻ
Tୟ୷ ൌ Tୠ୷ ൌ p. sଵ/ଶ ൌ 10,64 m ሺveriϐicaciónሻ
A B
Tay
a = 10 m
f
T0 T0
Tby
C
30 m
p = 0,5 kN/m