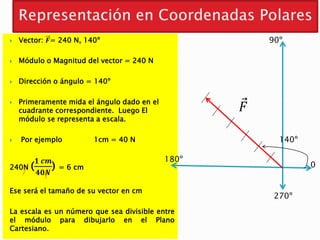
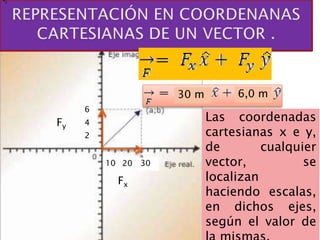
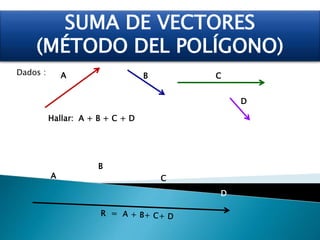
El documento describe las magnitudes escalares y vectoriales, así como su representación en coordenadas cartesianas y polares. Explica cómo calcular la suma de vectores utilizando diferentes métodos y la conversión entre coordenadas. Se incluyen ejemplos y fórmulas para determinar componentes y magnitudes de vectores en el plano cartesiano.

1. ¿Qué es una magnitud ESCALAR?
Es una cantidad que se puede
escribir mediante un Número y una
unidad de medida.
Temperatura: 27 ºC
Longitud: 5 m
Resumen
de las Pág.
112 a 126

2. 0º, 360º, E
90º, N
180º, O
270º, S
I
II
III IV
+

3. CANTIDADES VECTORIALES
Profesora

4. COORDENADAS POLARES DE UN
VECTOR
θ
O
𝒂 = 𝒂 , 𝜽

5.  Vector: 𝑭= 240 N, 140º
 Módulo o Magnitud del vector = 240 N
 Dirección o ángulo = 140º
 Primeramente mida el ángulo dado en el
cuadrante correspondiente. Luego El
módulo se representa a escala.
 Por ejemplo 1cm = 40 N
240N (
𝟏 𝒄𝒎
𝟒𝟎𝑵
) = 6 cm
Ese será el tamaño de su vector en cm
La escala es un número que sea divisible entre
el módulo para dibujarlo en el Plano
Cartesiano.
140º
0
90º
180º
270º
𝐹

6. 1) 𝒓 = 𝟑𝟓𝟎 𝒎, 𝟐𝟓𝟎º
2) 𝑽 = 𝟏𝟎𝟎
𝒌𝒎
𝒉
, 𝟑𝟓𝟎º
3) 𝒂 =
𝟐𝟎𝒎
𝒔𝟐 , 𝟑𝟎º al N del E
4) 𝑭 = 𝟓𝟎𝟎 𝑵, 𝟏𝟓º 𝒂𝒍 𝑶 𝒅𝒆𝒍 𝑵
5) 𝒓 = 𝟓 𝒎, 𝟗𝟎º
6) Los vectores del ejemplo 5.3 página
114.
a)Cada vector en coordenadas polares
represéntelo en el plano cartesiano.
(diapositiva 5)
b) Búsquele las coordenadas cartesianas
x e y. (diapositiva 10)
c) represéntelo en dichas coordenadas en
el plano cartesiano (diapositiva 10)
d) Finalmente pase las coordenadas
cartesianas del vector a polares
nuevamente. Las mismas deben coincidir
con las polares iniciales del vector.
(diapositiva 11)

7. Fx
Fy
Fy
Fy
Fy
Las coordenadas
cartesianas x e y,
de cualquier
vector, se
localizan
haciendo escalas,
en dichos ejes,
según el valor de
10 20 30
2
4
6
6,0 m
30 m

8. Magnitudes ESCALARES Magnitudes VECTORIALES
DIFERENCIA ENTRE ESCALAR Y
VECTOR EN EL PLANO CARTESIANO

9. CONVERSIÓN DE COORDENADAS
POLARES A CARTESIANAS Y VICEVERSA.
De polares a
cartesianas
De cartesianas
a polares
Con  medido en
contra de las
manecillas del reloj
con respecto al eje
x positivo de 0°
hasta los 360°
Módulo y Dirección
Coordenadas x e y
Páginas 116 a 119
𝑟𝑦
𝑟𝑥
𝐫 = 𝐫𝐱
𝟐 + 𝐫𝐲
𝟐

10.  𝐹 = 𝐹𝑥𝑥 + 𝐹𝑦𝑦
 𝐹𝑥 = 𝐹 cos 𝜃
 = (240N) cos 140º
𝐹𝑥 = - 184 N
 𝐹𝑦 = 𝐹 sin 𝜃
 = (240N) sin 140º
𝐹𝑦 = 154 N
 𝐹 = −184 𝑁 𝑥 + 154 𝑁 𝑦
100
200
154
-184
50
-100 -50
-150
-200
𝐹
Cada coordenada cartesiana
se representa en su propia
escala si es necesario.
150

11.  Para la dirección :
’ = 𝒕𝒂𝒏−𝟏(
𝑭𝒚
𝑭𝒙
)
’ = 𝒕𝒂𝒏−𝟏(
−𝟏𝟖𝟒 𝑵
𝟏𝟓𝟒 𝑵
)
’ = -39,9º = -40º
Modificación para el segundo
cuadrante
II.  = 180º - 40º
 = 140º
 Módulo del vector:
Teorema de Pitágoras
 𝑭 = 𝑭𝒙
𝟐 + 𝑭𝒚
𝟐

= (−𝟏𝟖𝟒 𝑵)𝟐+(𝟏𝟓𝟒 𝑵)𝟐
𝑭 = 239,9 N = 240 N
𝐹 = −184 𝑁 𝑥 + 154 𝑁 𝑦 debemos regresar a 𝑭= 240 N, 140º
𝑭= 240 N, 140º

12. SUMA DE VECTORES
(MÉTODO DEL PARALELOGRAMO)
A B
A
B
A
B
R R = A+ B

13. SUMA DE VECTORES
(MÉTODO DEL POLÍGONO PARA
DOS VECTORES)
A
B
A
R R = A+ B
B

14. A B C
Hallar: A + B + C + D
A B C
R
SUMA DE VECTORES
(MÉTODO DEL POLÍGONO)
Dados :
D
A
B
C
D

15. 1) Mida la dirección del primer
vector con el transportador.
Marque un punto en dicha
dirección.
2) Luego utilice una escala, (la
misma para todos los
vectores) y mida el módulo
del primer vector con su
regla, con el origen en el
primer plano cartesiano
dibujado y la punta de flecha
que pase por la dirección
señalada.
3) En la punta de flecha del
primer vector dibuje el
siguiente aplicando los
procedimientos 1 y 2 hasta
que termine con todos los
vectores.

16. A puede escribirse
A = Ax i + Ay j
SI NECESITAMOS SUMAR el
vector A = Ax i + Ay j con el vector B =
Bx i +By j
escribimos:
R = A + B = Ax i + Ay j + Bx i + By j =
(Ax + Bx)i + (Ay + By)j
Las componentes de R (=A + B) son
Rx = Ax + Bx y Ry = Ay + By
A
A
A
B
B
B
B
A
A
RECORDAR QUE i, j y k es igual a decir x, y z

17. Tres cuerdas están atadas a una estaca ejerciendo los siguientes
fuerzas. Obtener la fuerza RESULTANTE ejercida sobre la estaca.
R = A + B + C
A= 20 lb, 235°
B= 30 lb, 120°
C= - 44 lb – 22 lb ŷ
Receta de Cocina
1)Escribir álgebra vectorial de la operación a realizar.
2) Buscar todas las coordenadas cartesianas requeridas en el álgebra
vectorial.
3) Sustituir las coordenadas buscadas en el álgebra vectorial y encontrar
el vector resultante R en sus coordenadas cartesianas. Analizar en
qué cuadrante queda R según los signos de sus coordenadas
cartesianas.
4) Encontrar las coordenadas polares de R con el Teorema de Pitágoras
para el módulo y la tan inversa para la dirección.