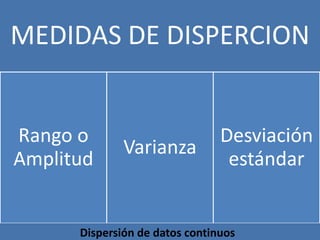
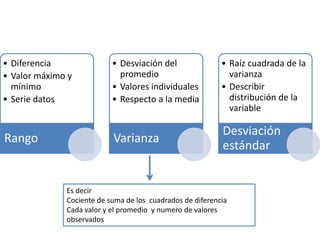
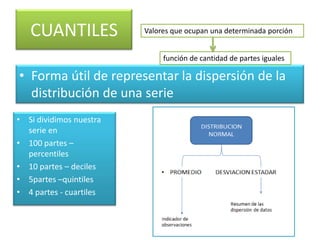
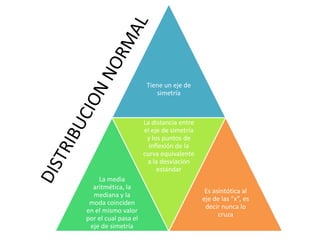
El documento aborda medidas de dispersión como rango, varianza y desviación estándar, centrándose en su aplicación a datos continuos y su cálculo a partir de observaciones. Se explica cómo estos conceptos ayudan a describir la distribución de variables y agrupar datos, destacando la importancia de los cuantiles para representar la dispersión. Además, se menciona la relación entre media, mediana y moda en contextos simétricos.

1. MEDIDAS DE DISPERCION
Rango o
Amplitud
Varianza
Desviación
estándar
Dispersión de datos continuos

2. • Diferencia
• Valor máximo y
mínimo
• Serie datos
Rango
• Desviación del
promedio
• Valores individuales
• Respecto a la media
• Raíz cuadrada de la
varianza
• Describir
distribución de la
variable
Varianza
Desviación
estándar
Es decir
Cociente de suma de los cuadrados de diferencia
Cada valor y el promedio y numero de valores
observados

3. • Periodo de incubación de la rubeola con base
a las 11 observaciones
• Media 19.7
• Varianza = (15-19.7)²+(15-19.7)²+..+(16-19.7) ² +….+(32-19.7) ² +(37-19.7) ²
11-1
• Varianza =572.19 = 57,219 días ²
10
Desviación estándar=
57,219
= 7,6 días

4. Datos variable
continua están
agrupados
Partimos puntos medios
Otra
columna
Y la media de
nuestros datos
Cada intervalo
R= multiplicación
desviación
cuadrática por
numero de casos
(f ) del intervalo
correspondiente
Calcular varianza y desviación
estándar aproximada
(X-Ẋ)
Desviación
cuadrática
(f (x-ẋ) ²)
suma de todos
productos
(∑ƒ(X–Ẋ)²)
Dividida entre la
suma de casos
(∑ƒ)
Razonable aproximación ala
varianza y extrayendo su raíz
cuadrada
Obtendremos un
estimado aceptable

5. • En este ejemplo la aproximación de la varianza seria :
• S²=∑ƒX–Ẋ)²= 1.022.763,25 = 229,47
X∑ƒ
4.457
DE. Para datos agrupados seria
D.E =
229,47 =15,1 AÑOS

6. CUANTILES
Valores que ocupan una determinada porción
función de cantidad de partes iguales
• Forma útil de representar la dispersión de la
distribución de una serie
• Si dividimos nuestra
serie en
• 100 partes –
percentiles
• 10 partes – deciles
• 5partes –quintiles
• 4 partes - cuartiles

7. Tiene un eje de
simetría
La distancia entre
el eje de simetría
y los puntos de
inflexión de la
curva equivalente
a la desviación
estándar
La media
aritmética, la
mediana y la
moda coinciden
en el mismo valor
por el cual pasa el
eje de simetría
Es asintótica al
eje de las “x”, es
decir nunca lo
cruza