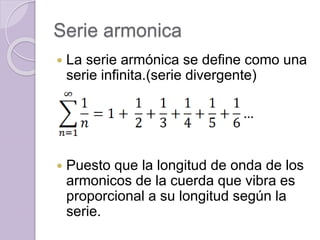
Una serie infinita es la suma de los términos de una sucesión infinita. Para determinar si una serie infinita converge o diverge, se considera la sucesión de las sumas parciales. Si la sucesión de sumas parciales converge a un límite cuando n tiende a infinito, la serie es convergente; de lo contrario, es divergente. Ejemplos de series incluyen series geométricas, la serie armónica (divergente) y series alternadas (potencialmente convergentes).

1. SERIES INFINITAS
Gregory Batista

2. ¿Que es una serie?
 Una serie es una es la
suma de los términos de
una sucesión. Esta se
representa con el termino
de an como la siguiente
figura siendo N el valor
final de la serie. Las
series infinitas es donde i
toma el valor de
absolutamente todos los
números naturales.
an= ∑N
i=1 ai

3. Series infinitas
 una aplicación importante de la sucesión
infinita es la representación de las sumas
infinitas. Informalmente si {an } es una
sucesión infinita, entonces:
∑∞
n=1 = a1 + a2 + a3 +…+ an
A esto se le llama una serie infinita. Los
números a1 , a2 , a3 , an son los términos
de la serie.

4. Sucesión de sumas parciales.
 Para encontrar la suma de una serie
infinita, se debe considerar la
siguiente sucesión de las sumas
parciales.
 S1= a1
 S2= a1 + a2
 S3= a1 + a2 + a3
 Sn= a1 + a2 +a3 + … + an

5. Continuación sucesión de
sumas parciales.
 La sucesión de sumas parciales Sn Para las
series.
, , , etc.
 La serie es convergente si su sucesión es de
su sucesión nos da un resultado =S tomando
como S que es la suma de la serie si S no
existe entonces se dice que la serie es
divergente.
 Un ejemplo de las sumas parciales seria

6. Continuacion sumas
parciales.
 Por fracciones parciales el termino
general “a” a la n de la serie se
puede escribir
de tal modo la suma parcial n-esima
de la serie toma todos los numeros
reales.

7. Definición de serie convergente y
divergente.
 Dada una serie infinita la n-esima
suma parcial esta dada por :
Si la sucesión de la suma parcial es { sn } converge a
S, entonces la serie es convergente esto significa
que sn tiende a un limite infinito.
Una serie divergente es una serie por lo cual los
términos individuales no tienden a cero. Un
ejemplo cuyos términos se aproximan a cero es la
serie armónica.
∑∞
n=1 = an
Sn= a1 + a2 +a3 + … + an

8. Serie geométrica
 Una serie geométrica
es una serie en la cual
cada termino se
obtiene multiplicando
el anterior por una
constante, a la cual
llamamos razón. La
razón Z, es
convergente, solo si
|z|<1, a:

9. Serie geométrica
continuacion
 Todo decimal repetido es una serie
geométrica convergente. Exprese el
decimal repetido 0.121212 como un
cociente de enteros 12/100 +12/10
000+ 12/1 000 000= 0.121212.

10. Serie armonica
 La serie armónica se define como una
serie infinita.(serie divergente)
 Puesto que la longitud de onda de los
armonicos de la cuerda que vibra es
proporcional a su longitud según la
serie.

11. Serie armonica
 También sabemos que es la suma por
los recíprocos de todos lo números
reales .

12. Serie alternada
 Es una serie donde los terminos
alteran el signo. Esta serie es
convergente.
 Ejemplo: