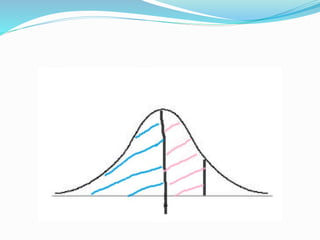
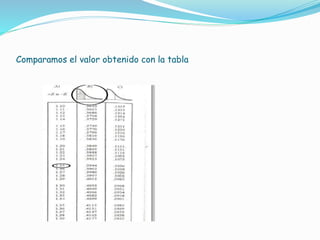
El documento describe un estudio sobre la autoestima de 500 mujeres que reciben asistencia. La autoestima se midió en una escala de 20 puntos con una media de 8 y desviación estándar de 2. Se busca calcular la probabilidad de que una mujer escogida al azar tenga una puntuación de 10.5 o menos en la escala, asumiendo una distribución normal. Para ello se tipifica el valor 10.5, se consulta la tabla normal y se obtiene una probabilidad del 89.44%.

1. Pilar Martínez Carmona
1º Enfermería Macarena
Estadística y TICs

2.  En una muestra de 500 mujeres que reciben
asistencia queremos saber como la pobreza afecta
a su autoestima.
 Medimos la autoestima con una escala de actitud
de 20 puntos (variable continua). Suponemos que la
distribución sigue una curva normal
 Media autoestima: 8
 Desviación típica: 2
 ¿Cuál es la probabilidad de que una destinataria de
asistencia seleccionada al azar tenga una
puntuación de 10.5 o menos en la escala de
autoestima?

3.  La curva normal permite comparar valores mediante el uso de
unas tablas ya establecidas, para ello hay que tipificar valores.
 Primero vamos a tificar, para averiguar la probabilidad del área
que está dentro de la curva. Para ello vamos a utilizar la siguiente
fórmula:

4.  Sabiendo que la media es 8, que la desviación típica es
2 y que el valor es 10,5, podremos hallar el valor
tificado: (10,5-8)/2= 1,25
 Vamos a representar la curva normal
 La línea de la izquierda representa el valor 10,5 y la de
la izquierda la media, que es 8
 Como en el ejercicio se nos piden también los menores
de 10,5, la campana de gauss vale 1 y la media se halla
en medio, después tendremos que sumarle al valor
obtenido 0,5-

6. Comparamos el valor obtenido con la tabla

7.  Tal y como podemos observar en la tabla, a 1.25 le corresponde
0.3944. A esto le sumamos el 0.5 que explicamos anteriormente y
obtendremos así un valor de 0.8944. Este valor lo multiplicamos
por 100 para obtener el porcentaje = 89.44%
 Podemos decir por tanto que la probabilidad de que una asistenta
al azar obtenga una puntuación de 10,5 es de 89,44%.