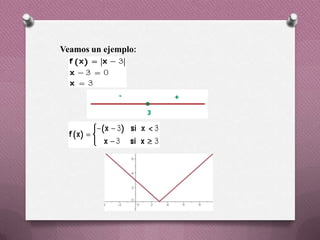
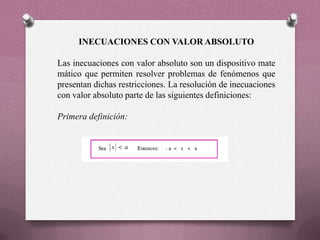
Este documento describe las propiedades y definiciones del valor absoluto. Explica que el valor absoluto de un número real es el propio número si es positivo, o su opuesto si es negativo. También define la distancia entre dos puntos como su diferencia en valor absoluto. Finalmente, cubre las propiedades fundamentales del valor absoluto como no negativa, definida positivamente y multiplicativa.

1. GARCÍA MADRID CLAUDIA L.
HERRERA DÍAZ HELEEN L.
Lic. Matemática y Física

2. EL VALOR ABSOLUTO Y SUS PROPIEDADES
Definición. El valor absoluto de un número real, a, es el
propio número a, si es positivo, o su opuesto, -a, si es
negativo:
Definición. Distancia entre dos puntos.
La distancia entre dos puntos “a” y “b” es su diferencia en
valor absoluto |a – b|.
Definición. |x|= máx. {x,-x}

3. El valor absoluto está relacionado con las nociones
de magnitud, distancia y norma en diferentes contextos
matemáticos y físicos.
La magnitud es una propiedad que poseen los fenómenos o las
relaciones entre ellos, que permite que puedan ser medidos; las
magnitudes matemáticas tienen definiciones abstractas,
mientras que las magnitudes físicas se miden con instrumentos
apropiados.
La distancia es la medida de la longitud del segmento que une
dos puntos de una trayectoria.
El valor absoluto es la distancia entre el origen y el punto que
representa un numero real n en la recta numérica, se llama
valor absoluto del número real n y se representa por │n│.

4. La función de valor absoluto tiene por ecuación f(x) = |x|. Su
gráfica va a estar siempre por encima de dicho eje o, a lo sumo,
tocándolo.
Las funciones en valor absoluto siempre representan una
distancia o intervalos (tramos o trozos) y se pueden resolver o
calcular siguiendo los siguientes pasos:
1. Se iguala a cero la función, sin el valor absoluto, y se calculan
sus raíces (los valores de x).
2. Se forman intervalos con las raíces (los valores de x) y se
evalúa el signo de cada intervalo.
3. Definimos la función a intervalos, teniendo en cuenta que en
los intervalos donde la x es negativa se cambia el signo de la
función.
4. Representamos la función resultante.

5. Veamos un ejemplo:

6. PROPIEDADES
FUDAMENTALES
No negativa.
Definición positiva
Propiedad multiplicativa
Desigualdad triangular

7. OTRAS
PROPIEDADES
simetría
Identidad de indiscernibles
Desigualdad triangular
(equivalente a la propiedad
adictiva)
Preservación de la división
(equivalente a la propiedad
multiplicativa)

8. Otras dos útiles inecuaciones son:
Estas últimas son de gran utilidad para la resolución
de inecuaciones, como por ejemplo:

9. INECUACIONES CON VALOR ABSOLUTO
Las inecuaciones con valor absoluto son un dispositivo mate
mático que permiten resolver problemas de fenómenos que
presentan dichas restricciones. La resolución de inecuaciones
con valor absoluto parte de las siguientes definiciones:
Primera definición:

11. Bibliografía
• http://www.vitutor.com/fun/2/c_12.html
• http://www.youtube.com/watch?v=Q4r8brqUFc
w
• http://planetmath.org/encyclopedia/AbsoluteValu
e.html
• http://es.wikipedia.org/wiki/Valor_absoluto