Tema F1 - Cinemática 1BACH

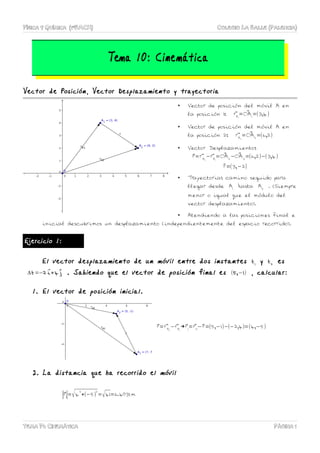
FÍSICA Y QUÍMICA (1ºBACH) COLEGIO LA SALLE (PALENCIA)
Tema 10: Cinemática
Vector de Posición, Vector Desplazamiento y trayectoria
• Vector de posición del móvil A en
la posición 1: ⃗rA1
= ⃗OA1
=(3,4)
• Vector de posición del móvil A en
la posición 2: ⃗rA2
= ⃗OA2
=(6,2)
• Vector Desplazamiento:
⃗r= ⃗rA2
− ⃗rA1
= ⃗OA2
− ⃗OA2
=(6,2)−(3,4)
⃗r=(3,−2)
• Trayectoria: camino seguido para
llegar desde A1
hasta A2
. (Siempre
menor o igual que el módulo del
vector desplazamiento).
• Atendiendo a las posiciones final e
inicial descubrimos un desplazamiento (independientemente del espacio recorrido).
Ejercicio 1:
El vector desplazamiento de un móvil entre dos instantes t1
y t2
es
Δt=−2 ⃗i+4 ⃗j . Sabiendo que el vector de posición final es (5,−1) , calcular:
1. El vector de posición inicial.
⃗r= ⃗rA2
− ⃗rA1
→⃗r1
= ⃗r2
−⃗r=(5,−1)−(−2,4)=(4,−5)
2. La distancia que ha recorrido el móvil
|⃗r1|=√4
2
+(−5)
2
=√41=6.4031 m
TEMA F1: CINEMÁTICA PÁGINA 1

Ejercicio 2:
El vector de posición de un móvil viene dado por la expresión
⃗r=t ⃗i +(5 −2 t )⃗j (unidades SI).
1. Construye una tabla con los valores de ⃗r correspondientes a t=0, 1, 2,
3 y 4 segundos. Represéntalos gráficamente. Dibuja la trayectoria
recorrida por el móvil y deduce si está
acelerando, frenando o si su velocidad es
constante.
t 0 1 2 3 4
⃗r (0,5) (1,3) (2,1) (3,-1) (4,-3)
Como la distancia entre puntos es la misma y el
intervalo de tiempo entre estos es siemre el mismo, podemos
concluir que el móvil se mueve a velocidad constante.
2. Calcula el desplazamiento entre t=0 y t=4 segundos así como la
distancia recorrida sobre la trayectoria en ese tiempo.
Δ⃗r=(4,−3)−(0,5)=(4,−8)→|Δ⃗r|=√4
2
+(−8)
2
=8.9443 m
Ejercicio 3:
El vector de posición de un móvil viene dado por la expresión
⃗r=(t
2
+1) ⃗i +3 ⃗j (unidade
s SI). Construye una
tabla con los valores
de ⃗r correspondientes
a t=0, 0.5, 1, 1.5 y 2
segundos. Represéntalos
gráficamente. Dibuja la
trayectoria recorrida
por el móvil.

Ejercicio 4:
Una canica rueda desde el
punto A hasta el punto D a lo
largo de una pista semicircular
de 5m de radio.
1. Calcula los valores de los
desplazamientos entre los
puntos A y B, A y C, A y
D.
7.07m, 9.23m, 10m
2. ¿Cuáles son los espacios recorridos entre dichos puntos?
7.85m, 11.78m, 15.7m

Vector Velocidad
El vector velocidad tiene la misma dirección que el desplazamiento
Vector velocidad Media
• ⃗vm
=
Δ⃗r
Δt
→(vm,x
, vm ,y
)=
(x−x0
Δt
,
y−y0
Δt )
• La dirección del vector velocidad media es la línea que une el punto inicial y el
punto final.
Vector velocidad instantánea
• Cuando el intervalo de tiempo es muy reducido: ⃗v=lim
Δt→0
⃗vm
=lim
Δt →0
Δ⃗r
Δt
• La dirección del vector velocidad instantánea es tangente a la trayectoria.
Celeridad o Rapidez
Se denomina así al módulo de la velocidad: |⃗v|=√vx
2
+vy
2
+vz
2
Ejercicio 5:
Un móvil parte del origen y al cabo de 20 segundos se encuentra en la
posición ⃗r=14 ⃗i−8 ⃗j . Calcula:
1. El desplazamiento producido en ese tiempo.
Δ⃗r=(14,−8)−(0,0)=(14,−8)→|Δ⃗r|=√14
2
+(−8)
2
=16.1245 m
2. El valor de la velocidad media del móvil.
⃗vm
=
Δ⃗r
Δt
=
(14,−8)
20
=(0.7,−0.4)→|⃗vm|=√0.7
2
+(−0.4)
2
=0.8062 m /s
3. La posición que ocupará dentro de otros 5s si continúa el movimiento
en las mismas condiciones.
Si la velocidad media es (0.7 ,−0.4) , implica que la velocidad en un segundo es:
⃗v1 s
=0.7 ⃗i−0.4 ⃗j
Entonces: ⃗r2
=⃗r1
+ ⃗vm
·t=(14⃗i−8 ⃗j)+(0.7 ⃗i−0.4 ⃗j)·5 s=14 ⃗i−8⃗j+3.5 ⃗i−2 ⃗j=17.5 ⃗i−10 ⃗j

Ejercicio 6:
Un cuerpo se desplaza en una recta según la ecuación ⃗r=5 t ⃗i+2 t ⃗j
¿Cuál es su velocidad en los cinco primeros segundos?.
⃗vm
=
Δ⃗r
Δt
=
(5 ·5 ⃗i+2 ·5⃗j)−(o ⃗i+0⃗j)
(5−0)
=5 ⃗i+2 ⃗j
Ejercicio 7:
Un cuerpo se mueve en línea recta desde el punto A(2,1) hasta el
punto B(5,7) en 0.1h (longitudes en Km). ¿Cuál ha sido su velocidad? ¿Cuál
es su valor exacto?
30 ⃗i+60 ⃗j(km/h) , 67km/h
Vector Aceleración
El vector aceleración sólo tiene la dirección de la
velocidad en el caso de que el movimiento sea rectilíneao.
Vector aceleración Media
• ⃗am
=
Δ ⃗v
Δt
→(am, x
, am, y
)=
(vx
−vx0
Δt
,
vy
−vy0
Δt )
Vector aceleración instantánea
• Cuando el intervalo de tiempo es muy reducido:
⃗a=lim
Δt →0
⃗am
=lim
Δt →0
Δ⃗v
Δt
Illustration 1: Fotografía
estroboscópica de dos objetos
cayendo

Componentes intrínsecas de la aceleración:
Aceleración tangencial
• Sólo produce cambios en el módulo de la velocidad:
◦ Módulo: ⃗at
=
Δv
Δt
⃗t
◦ Dirección: tangente a la trayectoria en cada punto.
◦ Sentido: a favor del movimiento o en contra (si el objeto se acelera o se frena
respectivamente).
Aceleración normal
• Sólo produce cambios en la dirección de la velocidad:
◦ Módulo: ⃗an
=
v
2
R
⃗n (caso de movimiento circular)
◦ Dirección: perpendicular a la trayectoria en cada punto.
◦ Sentido: hacia el centro de la circunferencia que el objeto describe en su
trayectoria.
Movimiento Circular
• Otra manera de describir el movimiento circular es medir los ángulos centrales que
recorre un ángulo de una
circunferencia.
◦ s=ϕ·R
• La velocidad angular es el ángulo
descrito por el radio que gira con el
móvil en la unidad de tiempo:
◦ ⃗ω=
Δϕ
Δt
• La aceleración angular es la variación
de la velocidad angular en cada
unidad de tiempo:
◦ ⃗α=Δω
Δt
• Periodicidad del movimiento:
◦ Período y frecuencia son magnitudes inversas
◦ T=
1
f
Illustration 2: Movimiento Angular

Ecuaciones de la Cinemática y Criterio de Signos
• Ecuaciones
◦ s=s0
+v0
·t+
1
2
a·t
2
◦ v=v0
+a·t
◦ v
2
−v0
2
=2 ·a·s
• Criterio de Signos
◦ Positivos: X hacia la derecha, Y hacia arriba
◦ Negativos: X hacia la izquierda, Y hacia abajo

Anexo I: Ejercicios para el trabajo personal
MRU
1. Un coche inicia un viaje de 495 Km a las 08:30 h. con una velocidad media de 90
Km/h. ¿A qué hora llegará a su destino?
2. Si la velocidad de la luz es de 300.000 km/s y el Sol se encuentra a 150.000.000 km
de distancia. ¿Cuánto tarda en llegar la luz del Sol a la Tierra?
3. Un ladrón roba una bicicleta y huye con ella a 20 km/h. Un ciclista que lo ve, sale
detrás de él tres minutos más tarde a 22 Km/h. ¿Al cabo de cuánto tiempo lo
alcanzará?
4. Dos puntos A y B distan entre sí 1600 m. A las 10 de la mañana salen dos ciclistas ,
uno de A hacia B y el otro desde B dirigiéndose hacia A, ambos con movimiento
rectilíneo y uniforme y velocidades respectivas de 8 y 12 m/s. ¿A qué distancia del
punto A se cruzarán? ¿Qué hora será cuando se crucen?
5. Un tren parte de una estación A a las 10 de la mañana y recorre con movimiento
uniforme los 28 km que separan la estación A de la B, llegando a ésta a las 10 horas
y 42 minutos. Después de una parada de 8 minutos, se pone en marcha a 48 km/h
(consideramos MRU) hacia la estación siguiente C, que dista 20 km de B.

1. Calcula la velocidad del tren en el recorrido entre A y B.
2. Calcula la hora de llegada del tren a C.
6. Un coche pasa por un semáforo con una velocidad de 50 Km/h. Una motocicleta pasa
5 s después por el mismo lugar a 60 Km/h. Si circulan por una calle recta, calcula:
1. La distancia en metros entre el semáforo y el punto en el cual la motocicleta
alcanza al coche.
2. El tiempo que tarda la motocicleta en alcanzar al coche.
7. Desde dos pueblos, A y B, separados por una distancia de 10 km, salen al encuentro dos
automóviles con velocidades de 72 km/h y 108 km/h. Calcula el tiempo que tardan en
encontrarse y su posición en ese instante, medida desde A.
8. Desde dos pueblos, A y B, separados 1 km, parten dos coches en el mismo instante con

velocidades constantes de 108 km/h y 36 km/h, en la misma dirección y sentido de A
a B. Calcula el tiempo que tardan en encontrarse y la distancia a la cual se
encuentran, medida desde A.
9. Un avión se ha desplazado 600Km hacia el norte, 1000Km hacia el sur y 500Km hacia
el norte. ¿Cuál ha sido el desplazamiento total del avión?
1. ¿Qué distancia ha recorrido?
2. ¿Cuál ha sido su velocidad media si ha empleado 5 horas en su recorrido?
10. Un empleado de un aeropuerto pone en marcha su cronómetro cuando una maleta está
situada a 3 metros del origen de una cinta transportadora rectilínea. La maleta es
arrastradadurante 10 segundos por la cinta, que se mueve a una velocidad constante
y hacia la derecha de 2 m/s.
1. Calcula la posición alcanzada por la maleta tras ese tiempo.

2. Determina el desplazamiento efectuado.
3. Representa las gráficas velocidad-tiempo y espacio tiempo del movimiento de la
maleta.
11. La ecuación de posición de un móvil es x (t)=2 t
2
+3 t . Determina la velocidad
media de éste móvil desde que empieza su movimiento (t=0s) hasta que pasan 3
segundos. Determina la expresión de su celeridad.
12. Calcula la velocidad media que ha mantenido un coche a lo largo de una
carretera rectilínea si ha recorrido 3km en 5 minutos. Da el resultado en m/s y en
km/s.
MRUA:
13. Un motorista que circula a 210 km/h frena con una aceleración constante de 1,5 m/s².
Calcula el tiempo que tarda en detenerse y la distancia que recorre hasta parar.
14. Un móvil que parte con velocidad inicial de 2 m/s y aceleración de 5 m/s² recorre
225 m. Calcula el tiempo empleado y la velocidad final que alcanza.

15. Un avión que parte del reposo, antes de despegar, recorre 547,2 m de pista con
aceleración constante durante 12 s. Calcula la aceleración y la velocidad de
despegue en km/h.
16. Un coche parte del reposo con una aceleración constante de 1 m/s² ¿Qué tiempo
necesita para recorrer 1000 m con dicha aceleración? ¿Qué velocidad llevará al cabo
de dicho tiempo?
17. Un tren parte del reposo en la estación A con una aceleración constante de 0,75
m/s2, que mantiene durante 50 s. Transcurrido dicho tiempo, mantiene la velocidad
alcanzada durante 6 minutos, tras lo cual frena durante 20 segundos, deteniéndose
en la estación B. ¿Cuál es la distancia entre las dos estaciones?
18. Un automóvil circula a 54 km/h cuando acelera para efectuar un adelantamiento.
Si la aceleración es igual a 4,5 m/s² y completa el adelantamiento en una
distancia de 250 m. Calcula la velocidad del automóvil al finalizar el
adelantamiento y el tiempo durante el cual está adelantando.
19. Un coche pasa por un punto A con velocidad constante de 80 km/h. Un motorista sale
de A 5 segundos después en la misma dirección y sentido que el coche y con
aceleración constante de 6 m/s². Calcula la distancia de A a la que la moto
alcanza al coche y el tiempo que tardan en encontrarse a partir de la salida del
motorista.

20. Un tren de mercancías entra en un túnel recto de doble vía de 1 km de longitud
con velocidad constante de 43,2 km/h. En ese mismo instante, desde el otro extremo
del túnel parte del reposo en sentido contrario un tren de viajeros con aceleración
de 1,5 m/s². Calcula la distancia a la cual se encuentran, medida desde el primer
extremo del túnel y la velocidad del tren de viajeros cuando se cruzan.
21. En el momento en que un semáforo cambia a verde, un automóvil se pone en marcha
con aceleración constante de 2 m/s². En ese mismo instante, el automóvil es
adelantado por una motocicleta que circula a una velocidad constante de 57,6
km/h. Calcula la distancia, medida desde el semáforo, a la cual el coche alcanza
a la motocicleta y la velocidad del coche en el instante del encuentro.
22. Un conductor que viaja de noche a una velocidad de 100km/h ve, de repente, las
señales que le indican la roximidad de una valla a 40 metros en medio de la
calzada. Tarda 0.75 segundos en pisar el edal del freno. Si la deceleración máxima
del pedal de freno es de 10m/s². Calcula si chocará contra la valla.
1. Si es así, ¿a qué velocidad?
2. ¿Cuál será la velocidad máxima a la que puede ir un automóvil sin que
colisione con la valla?

23. Un tren entra en un puente rectilíneao de 3Km de longitud con una velocidad de
20m/s y una aceleración de 1m/s². Tres segundos más tarde, entra por el otro extremo
del puente, y en la vía contigüa, un AVE (Alta Velocidad Español) con una velocidad
de 60m/s y una aceleración de 3m/s². Escribir las ecuaciones de movimiento de
ambos trenes.
1. Calcula el instante y la posición en la que se cruzan:
2. Calcula la velocidad de cada tren cuando se cruzan.
24. Un camión y un automóvil inicial el movimiento en el mismo instante, en la
misma dirección y sentido desde dos semáforos contigüos en la misma calle. El
camión tiene una aceleración de 1.2m/s² mientras que el automóvil acelera con
2.4m/s². El automóvil alcanza al camión tras recorrer 50 metros. ¿Cuánto tiempo tarda
el automóvil en alcanzar al camión?
1. ¿Qué distancia separa los dos semáforos?
2. ¿Qué veocidad posee cada vehículo cuando están emparejados?

Caída libre:
25. Desde una altura de 7 m lanzamos hacia arriba una pelota con una velocidad
inicial de 40 m/s. Calcula la altura máxima que alcanza, medida desde el suelo, y
el tiempo que tarda en alcanzarla.
26. Desde una ventana a 20 m de altura, se lanza verticalmente hacia abajo una
pelota con una velocidad de 4 m/s. Calcula el tiempo que tarda en llegar al suelo
y la velocidad con la que llega.
27. Un muchacho trata de lanzar verticalmente un balón desde la acera de la calle a
su hermana, que se encuentra asomada a la ventana de su casa, a 15 m de altura.
Calcula la velocidad con que debe lanzar el balón para que lo alcance su
hermana.
28. Desde una ventana, situada a 15 m de altura, se deja caer un balón. Al mismo
tiempo, desde el suelo, se lanza verticalmente hacia arriba una piedra con una
velocidad inicial de 12 m/s. Calcula la posición de ambos objetos cuando se
encuentran y el tiempo que tardan en encontrarse.
29. Desde el suelo se lanza verticalmente y hacia arriba una pelota. A través de una
ventana situada en el tercer piso, a 9 m del suelo, un vecino la ve pasar con una
velocidad de 5 m/s. Calcula la velocidad con la que fue lanzada, la altura
máxima que alcanza y el tiempo que tarda en llegar a la ventana.

30. Desde una azotea a 20 m de altura desde el suelo se lanza hacia arriba una piedra
con velocidad de 25 m/s. Al mismo tiempo, desde el suelo, se lanza otra piedra,
también hacia arriba, con una velocidad de 30 m/s. Calcula la distancia del suelo
a la que se cruzan, el tiempo que tardan en cruzarse y las velocidades de cada
piedra en ese instante.
31. Se lanza verticalmente hacia arriba una pelota, con velocidad de 12 m/s (g=10m/s²).
Determinar la altura máxima alcanzada y la velocidad cuando se encuentre a 6 m
de altura. Justificar por qué, para que el cuerpo se encuentre a 6 m de altura, se
obtienen dos valores distintos del tiempo.
32. Se lanza una bola hacia arriba desde el suelo con una velocidad de 30 m/s. (g = 10
m/s²) ¿Cuánto tarda en llegar al punto más alto? ¿Qué altura máxima alcanzará?
¿Cuánto tiempo tardará en llegar al suelo de nuevo? ¿Cuál será la velocidad con
que llegará al suelo?
33. Desde un puente sobre un arroyo un excursionista lanza una piedra verticalmente
hacia arriba a la velocidad inicial de 6m/s.
1. ¿Hasta qué altura se eleva la piedra?
2. ¿Cuánto tarda en volver a pasar por el nivel del puente? ¿Con qué velocidad lo

hace?
3. Si la piedra cae al río 1,94 s después de lanzarla ¿qué altura hay desde el puente
a la superficie del agua?
4. ¿Con qué velocidad llega la piedra al agua?
5. ¿Cuánto tardaría el excursionista en llegar al agua si se dejara caer desde el
puente?
34. Desde lo alto de una torre de altura h se deja caer u objeto. ¿A qué distancia
tendrá una velocidad igual a la mitad que tiene cuando llegue al suelo?
35. Lanzas un cuerpo verticalmente hacia arriba, de forma que tiene una velocidad de
8m/s cuando ha alcanzado la mitad de la altura máxima a la que puede subir. ¿Con
qué velocidad se lanzó?

1. ¿A qué altura sube?
2. ¿Qué velocidad posee un segundo después de ser lanzado?
36. Se deja caer una piedra desde el brocal de un pozo y tarda 2.3 segundos en
percibirse el sonido producido por el choque con el agua. Si la velocidad del sonido
en el aire es de 340m/s. ¿A qué profundidad está el agua?
Composición de Movimientos
37. Deseamos cruzar un río de 200 m de ancho. Si la velocidad de la corriente es de 4
m/s y nuestra barca desarrolla una velocidad de 9 m/s perpendicular a la corriente,
calcula la velocidad de la barca respecto de un sistema de referencia fijo en la
orilla.
1. El tiempo que tarda en atravesar el río.
2. La distancia recorrida por la barca.

38. Una barca pretende cruzar un río de 150 m de ancho con una velocidad de 12 m/s
perpendicular a la corriente. La velocidad de la corriente es de 10 m/s. Calcula el
tiempo que tarda y la distancia que recorre.
39. Un barquero desea cruzar un río de 100 m de ancho con una barca cuyo motor
desarrolla una velocidad de 3 m/s perpendicularmente a una corriente de 1 m/s.
Calcula el tiempo que tarda en atravesar el río, la velocidad de la barca y la
distancia que recorre.
40. Un proyectil es lanzado desde lo alto de un acantilado de 150 m de altura con una
velocidad inicial de 400 m/s y con un ángulo de inclinación de 30º. Determina
las componentes de la velocidad inicial.
1. El tiempo que tarda en caer al suelo.
2. El alcance y la altura máxima.
41. Un futbolista chuta hacia la puerta con una velocidad de 15 m/s. Calcula el
alcance para un ángulo de tiro de 30º, 45º y 60º.

1. El tiempo que el balón permanece en el aire en cada uno de los lanzamientos.
42. Un proyectil sale despedido desde el suelo con una velocidad de 200 m/s y un ángulo
de inclinación de 45º. A 565 m del punto de lanzamiento hay una pared. Calcula
cuál debe ser la altura máxima de la pared para que el proyectil pase por encima.
43. Un esquiador salta desde una altura de 20 m con una velocidad horizontal de 80
km/h. Calcula el tiempo que está en el aire y el alcance que consigue, medido
desde el trampolín.
44. Un joven lanza piedras horizontalmente desde lo alto de un acantilado de 25 m de
altura. Si desea que choquen contra un islote que se encuentra a 30 m de la base
del acantilado, calcula la velocidad con que debe lanzar las piedras y el tiempo
que tardan en chocar contra el islote.
45. Se dispara un proyectil desde el suelo con una velocidad inicial de 540 m/s y un
ángulo de inclinación de 30º respecto a la horizontal. Calcula el alcance del
proyectil y la posición 3 s después del lanzamiento.
46. Un lanzador de jabalina consigue lanzar una distancia de 90 m con un ángulo de
inclinación de 45º. Calcula la velocidad de lanzamiento y el tiempo que estuvo en
el aire.

47. Una jugadora de baloncesto pretende anotar un triple y para ello lanza una pelota
desde una distancia de 6.5 metros a una altura de 1.9 metros del suelo. Si la
canasta está a una altura de 2.5 metros del suelo, ¿con qué velocidad debe realiza
el tiro si lo hace con un ángulo de elevación de 30º?
Coordenada x Coordenada y
Ecuaciones x=x0+v0 x ·t
y=y0+v0 y ·t+
1
2
·ay ·t
vy=v0 y+ay ·t
Canasta 6,5=v0 ·cos 30º ·t
2,5=1,9+v0 ·sen30º·t−
1
2
·9,81·t
2
vy=v0·sen 30º−9,81·t
Con las dos primeras ecuaciones planteo un sistema de ecuaciones para obtener la
velocidad inicial de la pelota:
{
6,5=v0·cos30º ·t
2,5=1,9+v0· sen30º·t−
1
2
·9,81·t
2 →
{t=0,8017 s
v0=9,362m/ s
48. Una pelota de beisbol abandona el bate a una altura de 1.0 metros por encima del
suelo y con un ángulo de elvación de 45º, con una velocidad tal que el alcance
horizontal hubiera sido de 100m. A la distancia de 90m del punto de lanzamiento se
encuentra con una valla de 8m de altura. ¿Pasará la pelota por encima de la valla?
Coordenada x Coordenada y
Ecuaciones x=x0+v0 x ·t
y=y0+v0 y ·t+
1
2
·ay ·t
vy=v0 y+ay ·t
A los 100m 100=v0·cos 45º·t100m
0=1+v0 ·sen45º ·t100 m−
1
2
·9,81·t100m
2
vy=v0·sen 45º−9,81·t100 m
A los 90m 90=v0 ·cos45º ·t90 m
y90m=1+v0·sen 45º·t90m−
1
2
·9,81·t90m
2
vy=v0 ·sen45º−9,81·t90m
Con las ecuaciones a los 100m planteo un sistema de ecuaciones para obtener la
velocidad inicial de la pelota.:
{
100=v0·cos 45º·t100m
0=1+v0·sen 45º ·t100m−
1
2
·9,81·t100 m
2 →
{t100 m=4,5377s
v0=31,1659m/s

Una vez conocida la velocidad inicial de la pelota la introduzco en las
ecuaciones a los 90m para obtener la altura de la pelota con esa coordenada:
{
90=31,1659·cos45º ·t90m
y=1+31,1659·sen45º ·t90 m−
1
2
·9.81·t90m
2 →
{t90 m=4,0839s
y90 m=9,1927m
Como la valla mide 8m, concluimos que la pelota pasa por encima de la misma.
Movimiento circular:
49. Un disco de 15 cm de radio gira a 45 revoluciones por minuto. Calcula la velocidad
angular en rad/s.
1. La velocidad lineal en punto de la periferia del disco.
2. El número de vueltas que da el disco en 30 min.
50. Un disco de 15 cm de radio gira a razón de 33 rpm. Calcula la velocidad angular
en rad/s, la velocidad lineal de un punto de la periferia y las vueltas que da en 5
min.
51. Un tocadiscos gira a 90 rpm. Halla su velocidad angular (rad/s) y calcula su periodo
y frecuencia.

52. Una rueda de 0,5 m de radio gira a 300 rpm en el momento que actúa un freno que
la detiene en 5 s. Calcula la velocidad angular inicial en rad/s.
1. El número de vueltas que da el volante hasta detenerse.
2. La aceleración tangencial en un punto de la periferia.
3. La aceleración normal de este mismo punto cuando el volante gira a 300 rpm.
53. La acción de un freno es capaz de detener un coche, cuyas ruedas giran a 300 rpm,
en 10 s. Calcula la aceleración angular.
1. La velocidad angular a los 4 s de comenzar a frenar.
2. El número de vueltas que da una rueda cualquiera desde que comienza a actuar
el freno hasta que se detiene totalmente.

54. Un disco de 15 cm de radio, inicialmente en reposo, acelera uniformemente hasta
alcanzar una velocidad angular de 5 rad/s en 1 min. Calcula la aceleración
angular del disco.
1. La velocidad lineal de un punto de la periferia a los 25 s de iniciarse el
movimiento.
2. La aceleración tangencial de un punto del borde del disco.
3. El número de vueltas que da el disco en un minuto.
55. Un móvil describe una trayectoria circular de 1m de radio 30 veces por minuto.
Calcula el período y la frecuencia de este movimiento.
1. Calcula la velocidad angular
2. La velocidad tangencial y la aceleración centrípeta de este movimiento.

56. Un ventilador gira a 360rpm (revoluciones por minuto). En un momento dado se
desenchufa de la corriente y tarda 35s en pararse. Calcula su aceleración angular:
1. ¿Con qué velocidad gira 15 segundos después de desenchufarlo?
2. ¿Cuántas vueltas da hasta que se para?
57. Un punto material describe una circunferencia de 2m de radio con aceleración
constante. En un punto A de la trayectoria la velocidad es de 0.5m/s y transcurridos
2 segundos la velocidad en otro punto es de 0.75m/s. Calcula la velocidad angular
en ambos puntos.
1. La aceleración tangencial y angular de la partícula.
2. La aceleración normal en ambos puntos.
58. Un ciclista parte del reposo en un velódromo circular de 50 m de radio. Va

moviéndose con movimiento uniformemente acelerado hasta que, a los 50 segundos
de iniciada la marcha, alcanza una velocidad de 36Km/h. Y desde ese momento
conserva su velocidad. Calcula: la aceleración tangencial y la aceleración
angular en la primera etapa del movimeinto.
1. La aceleración normal y la distancia recorrida en el momento de cumplirse los
50 segundos.
2. El tiempo que tarda en dar una vuelta cuando va a velocidad constante.
3. El número de vueltas que da en 10 minutos contados desde que inició el
movimiento.
59. Una lavadora cuyo tambor tiene un radio de 25 cm centrifuga a 600 vueltas por
minuto. Calcula la velocidad angular en rad/s.
1. Halla la aceleración centrípeta de la ropa que “se queda pegada” al tambor
durante el centrifugado.

60. Un CD de 6cm de radio gira a una velocidad angular de 261.8 rad/s. Al apagar el
lector, el CD tarda 8 s en detenerse. Calcula la aceleración angular y la
tangencial en un punto de la periferia del CD. Calcula las vueltas que da antes
de pararse.
{ϕ=ϕ0+w0 ·t−
1
2
·α·t
2
w=w0+α·t
→
{ϕ=0+261,8·8+
1
2
·α·8
2
0=261,8+α·8
→
{ϕ=1047,2rad
α=−32,725rad/ s
2
Corresponde a :
1047,2
2·π
=166,6667 vueltas
1. La velocidad angular a los 2 segundos de comenzar a detenerse.
w2s=w0+α·2=261,8−32,725·2=196,35rad/s

Soluciones:
1. 14:00.
2. 500s.
3. Tiempo ciclista:30 min
4. 640 m; 10:01:20.
5. 40 km/h; 11:15.
6. 416,7 m; 30 s
7. 200 s; 4000 m
8. 50 s; 1500 m
9. 100Km N; 2100 Km;
20Km/h N
10. 23m; 20m.
11. 9m/s. √4 t
4
+9t
2
12. 36Km/h; 10m/s
13. 38,9 s; 1134,1 m
14. 9,1 s; 47,5 m/s.
15. 7,6 m/s²; 328,3 km/h.
16. 44,72 s; 44,72 m/s.
17. 14,98km.
18. 49,7 m/s; 7,7 s.
19. 351,7 m; 10,8 s.
20. 352,6 m; 44 m/s.
21. 256 m; 32 m/s.
22. 88,6 m; 4,1 s.
23. 20t +
1
2
t
2
;
3000−60(t−3)−
1
2
·3 ·(t−3 )
2
; 25,8 s; 848,8m; 45.8m/s;
-128,4m/s
24. 71km/h; 78 km/h.
25. 9.1s; 50m; 39Km/h; 79Km/h.
26. 1,7 s; 20,2 m/s.
27. 17,1 m/s.
28. 7,3 m; 1,25 s.
29. 14,2 m/s; 10,3 m; 0,9 s.
30. 41,6 m; 4 s; 14,2 m/s y 9,2
m/s.
31. 7,2 m; 4,89 m/s.
32. 3 s; 45 m; 6 s; 30 m/s.
33. 1,84 m; 1,22 s, 6 m/s 6,86 m;
13,06 m/s; 1,18 s.
34. 9,8 m/s; 22,2 s; 218,8 m.
35. ¾h
36. 11m/s; 6.5m; 1.5m/s
37. 24m.
38. 12,5 s; 195,3 m.
39. 33,3 s; 3,2 m/s; 105,4 m.
40. V0x = 346,4 m/s,V0y = 200
m/s; 41,5 s; 14376 m; 2190,8
m.
41. 19,9 m; 23 m; 19,9 m; 1,5 s;
2,2 s; 2,7 s.
42. 487,2 m.
43. 2 s; 44,4 m.
44. 13,3 m/s; 2,2 s.
45. 25768,7 m; x = 1403 m, y =
765,9 m.
46. 29,7 m/s; 4,3 s.
47. 9.4m/s.
48. Sí pasará
49. 1,5 rad/s; 0,7 m/s; 1350π
rev.
50. 1,1 rad/s; 0,5 m/s; 165π
vueltas.
51. 3 rad/s; 0,67 s; 1,5 Hz.π
52. 10 rad/s; 12,5 rev; – 3,1π
m/s²; 493,5 m/s².
53. – rad/s²; 6 rad/s; 25π π
vueltas.
54. 0,08 rad/s²; 0,3 m/s; 0,01
m/s²; 22,9 vueltas.
55. 2s;0,5Hz;3.14rad/s; 3.14m/s;
9.9m/s²
56. -1.1 rad/s²; 22 rad/s; 105
vueltas.
57. 0.25 rad/s; 0.37 rad/s;
0.13m/s²; 0.063m/s²; 0.13 m/s²;
0.28m/s².
58. 0.2m/s²; 0.004 rad/s²; 2m/s²;
250 m; 31 s; 18 vueltas.
59. 62.83 rad/s; 987 m/s²
60. -32.73 rad/s²; -196.38 cm/s²;
166.6 vueltas; 196.34 rad/s

Tema F1 - Cinemática 1BACH

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (9)

Similar a Tema F1 - Cinemática 1BACH

Similar a Tema F1 - Cinemática 1BACH (20)

Más de David Saura

Más de David Saura (11)

Último

Último (20)

Tema F1 - Cinemática 1BACH