S

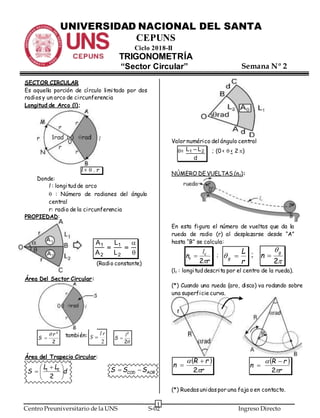
1. 1
Centro Preuniversitario de la UNS S-02 Ingreso Directo
UNIVERSIDAD NACIONAL DEL SANTA
CEPUNS
Ciclo 2018-II
TRIGONOMETRÍA
“Sector Circular”
SECTOR CIRCULAR
Es aquella porción de círculo limitado por dos
radiosy un arco de circunferencia
Longitud de Arco (l);
l =  . r .
Donde:
l : longitudde arco
 : Número de radianes del ángulo
central
r: radio de la circunferencia
PROPIEDAD:



2
1
2
1
L
L
A
A
(Radio constante)
Área Del Sector Circular:
2
2
r
S

 también:
2
rl
S 
2
2
l
S
Área del Trapecio Circular:
d
LL
S 




 

2
21
AOBCOD SSS 
Valor numérico del ángulo central
=
d
LL 21  ; (0 <  < 2 )
NÚMERO DE VUELTAS (nv):
En esta figura el número de vueltas que da la
rueda de radio (r) al desplazarse desde “A”
hasta “B” se calcula:
r
n c
v
2
l
 ;
r
L
g  ;


2
g
n 
(lc : longituddescrita por el centro de la rueda).
(*) Cuando una rueda (aro, disco) va rodando sobre
una superficie curva.
 
r
rR
n


2


 
r
rR
n


2


(*) Ruedasunidaspor una faja o en contacto.
Semana Nº 2

2. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
2
Centro Preuniversitario de la UNS S-02 Ingreso Directo
Se cumple:
1r1 = 2r2
n1r1 = n2r2
L1 = L2
(*) Ruedas unidadespor sus centros.
Se cumple: 1 = 2 n1 = n2
2
2
1
1
r
L
r
L

Propiedad
PROBLEMA DECLASE
1. Si AOB y MON son sectores circulares
y OM=1u, calcule AM.
A) 2 u
B) 3 u
C)
3
2
𝑢
D) 1 u
E) 2/3 u
2. En la figura, el área del sector circular
AOT es igual al área del sector circular
MOB. Si 𝑂𝐴 =
𝑂𝐵
2
, halle la medida del
ángulo BOT.
A) 30º
B) 36º
C) 24º
D) 38º
E) 40º
3. Calcule el perímetro de la región
sombreada si AOB es un sector
circular de radio r=2 u.
A)(
𝜋
2
+ 2√2 − 2) 𝑢
B) (
𝜋
4
+ 2√2 − 2) 𝑢
C) (
𝜋
2
+ √2 − 1) 𝑢
D) (
𝜋
4
+ √2 − 1) 𝑢
E) (
𝜋
2
+ 2√2 − 1) 𝑢
4. En la figura, AOB y COD son sectores
circulares. Halle el área del trapecio
circular ABCD si AD=3u.
A)
5𝜋
2
𝑟𝑎𝑑
B)
15𝜋
4
𝑟𝑎𝑑
C)
5𝜋
4
𝑟𝑎𝑑
D)
3𝜋
2
𝑟𝑎𝑑 E)
15𝜋
2
𝑟𝑎𝑑
5. La bolita se deja caer a partir del
punto A y recorre las longitudes de
arco 𝑙1 𝑦 𝑙2 hasta llegar al punto C.
Calcule PA si 𝑙1 + 𝑙2 =
4𝜋
3
𝑢 𝑦 𝑃𝑄 = 6𝑢
A) 5,4 u
B) 6,8 u
C) 6,5 u
D) 7 u
E) 6,3 u
0
R
S
R R R R
R
R
R
3S
5S
7S

3. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
3
Centro Preuniversitario de la UNS S-02 Ingreso Directo
6. Si AOB, MON y ROP son sectores
circulares, calcule n – x.
A) 2
B) 1
C) – 1
D)
1
2
E) – 2
7. En el gráfico, 𝑙1 + 𝑙2 =
5𝜋
6
𝑟.
Halle 𝑙2 − 𝑙1. Considere que
𝑙1: longitud del arco 𝐴𝐴′̂
𝑙2: longitud del arco 𝐵𝐵̂ ′
A)
2𝜋
3
𝑟
B)
𝜋
3
𝑟
C)
𝜋
4
𝑟
D)
𝜋
2
𝑟
E)
𝜋
6
𝑟
8. Los radios de las ruedas de una
bicicleta son entre sí como 3 es a 5.
Calcule el número de vueltas que da la
rueda menor cuando la rueda mayor
barre un ángulo de 216𝜋 𝑟𝑎𝑑𝑖𝑎𝑛𝑒𝑠.
A) 108 B) 200 C) 180 D) 220 E) 360
9. Si AOB es un sector circular y
𝑙 𝐸𝐵̂ = 9𝜋 𝑐𝑚, calcule 𝑙 𝐴𝐸̂
A) 18𝜋 𝑐𝑚
B) 24𝜋 𝑐𝑚
C) 16𝜋 𝑐𝑚
D) 20𝜋 𝑐𝑚
E) 10𝜋 𝑐𝑚
10. Del gráfico mostrado se cumple que
AOB y COD son sectores circulares,
𝑙 𝐴𝐵̂ − 𝑙 𝐶𝐷̂ = 6, 𝐴𝐶 =
3
2
𝑦
𝑙 𝐶𝑀̂ − 𝑙 𝑀𝑁̂ = 𝑙 𝑁𝐷̂ . 𝐶𝑎𝑙𝑐𝑢𝑙𝑎𝑟 𝜃
A) ¾ B) 1 C) 2 D)
5
3
E)
1
2
11. En los sectores circulares AOB y COD,
𝑙 𝐴𝐵̂ = 𝑎√3 𝑢 𝑦 𝑂𝐶 = 𝑏 𝑢 . Calcule
𝑚∡ 𝐴𝑂𝐵.
S: área del sector circular COD.
A)
𝑎
𝑏
B)
𝑏
𝑎
C)
𝑎
2𝑏
D)
𝑏
2𝑎
E)
2𝑎
𝑏
12. Si la rueda que se muestra en el
gráfico barre un ángulo de 750º al ir
de A hasta B, calcule el radio de la
rueda.
A)
90
25𝜋+6
B)
180
25𝜋+7
C)
9
2𝜋+1
D)
180
25𝜋+6
E)
90
24𝜋+5
13. Determine el número de vueltas que
dará la rueda de radio 8 u al
desplazarse desde A hasta tocar la
pared vertical ( 𝜋 =
22
7
).
A) 3 B) 4 C) 6 D) 7 E) 8

4. Lic. Rodolfo Carrillo Velásquez WWW.lobo-de-fama.blogspot.com Trigonometría.
4
Centro Preuniversitario de la UNS S-02 Ingreso Directo
14. Calcule el número de vueltas que da la
rueda de radio igual a 𝑟 = 1 u al ir
desde la posición A hasta la posición B.
A) 1 B) 2 C) 2,5 D) 1,5 E) 3
15. En la figura, se muestra una rueda que
gira sobre una superficie circular.
Determine el número de vueltas que
ha dado la rueda para ir desde P hasta
Q si su radio es 1/6 del radio de la
superficie circular sobre la cual se
desplaza.
A) 1,8
B) 2,0
C) 2,3
D) 2,5
E) 1,5
16. Dos ruedas de radios R y r, tal que
𝑅 > 𝑟, recorren la misma longitud L
sobre una pista plana. Si la diferencia
del número de vueltas de la menor y la
mayor es
𝐿
𝜋𝑅
, calcule
𝑅
𝑟
.
A) 6 B) 2 C) 3 D) 4 E) 5
17. Sobre una superficie curva de radio R
gira una rueda cuyo radio es r. Si dicha
rueda da 2 vueltas al ir de A a B,
calcule la longitud del arco AB.
A)
2𝜋𝑅𝑟
𝑅−𝑟
B)
4𝜋𝑅𝑟
𝑅−𝑟
C)
2𝜋𝑅𝑟
𝑅+𝑟
D)
4𝜋 𝑅2
𝑅−𝑟
E)
4𝜋 𝑟2
𝑅−𝑟
18. Las ruedas de radios 1 u y 4 u dan 10
y 3 vueltas, respectivamente, desde su
posición inicial hasta el instante en
que se separan. Calcule la distancia
que las separa.
A) (44𝜋 + 3) 𝑢 B) (34 𝜋 +4) u
C) (22 𝜋 +2) u D) (44 𝜋 +4) u
E) (24 𝜋 +4) u
19. En el gráfico, determine el número de
vueltas que da la rueda de radio igual
a 1 u al ir desde A hasta C. Considere
que AB=12 u y BC=8 u.
A)
𝜋+60
2𝜋
B)
𝜋+60
2𝜋
C)
𝜋+60
2𝜋
D)
𝜋+60
2𝜋
E)
𝜋+60
2𝜋
20. Una rueda de radio a metros da 10
vueltas para recorrer un tramo de
longitud L metros. Otra rueda de radio
(𝑎2
+ 62𝑎–3) metros gira 60º para
recorrer el mismo tramo. Calcule
𝑎2
+ 2𝑎 en metros.
A) 3 m B) 2 m C) 6 m D) 1 m E) 8 m