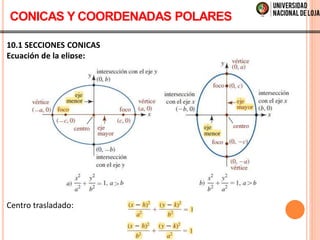
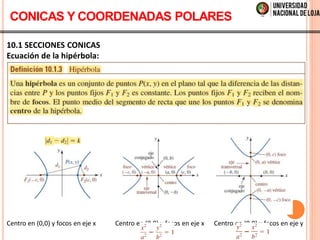
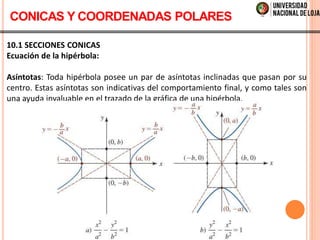
El documento aborda el cálculo vectorial, centrándose en secciones cónicas y ecuaciones paramétricas. Se describe la intersección de un doble cono con un plano, así como las ecuaciones de curvas como círculos, parábolas, elipses e hipérbolas. También se presenta el sistema de coordenadas polares y la conversión entre coordenadas polares y rectangulares, junto con métodos para calcular áreas en coordenadas polares.

1. CALCULO VECTORIAL
PARTE I
Jorge Patricio Muñoz Vizhñay
Ing. Eléctrico, MSc. , MBA
FACULTAD DE ENERGÍA, LAS
INDUSTRIAS Y LOS RECURSOS
NATURALES NO RENOVABLES
CARRERA DE
INGENIERÍA
ELECTROMECÁNICA

2. Contenido:
Secciones cónicas
Ecuaciones paramétricas
Cálculo y ecuaciones paramétricas
Sistema de coordenadas polares
Gráficas de ecuaciones polares
Cálculo en coordenadas polares
CONICAS Y COORDENADAS POLARES

3. 10.1 SECCIONES CONICAS
Introducción: Las curvas que se obtienen al intersecar un doble cono con un plano:
el círculo, la parábola, la elipse y la hipérbola. Ver Figura de las cuatro secciones
cónicas. Al finalizar el periodo griego se desvaneció el interés en las secciones
cónicas; después de Hipatia el estudio de estas curvas fue ignorado durante 1 000
años.
Cada una de estas ecuaciones estará en la forma de una ecuación cuadrática en las
variables x y y:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
donde A, B, C, D, E y F son constantes.
CONICAS Y COORDENADAS POLARES

4. 10.1 SECCIONES CONICAS
Ecuación de un círculo: La forma estándar de un círculo con centro (h, k) y radio r,
(x - h)2 (y - k)2 = r2
Ecuación de la parábola: Para describir una parábola analíticamente, supondremos
en aras de la discusión que la directriz L es la recta horizontal y = - p y que el foco
es F(0, p). Utilizando la definición 10.1.1 y la Figura, observamos que d(F,P)=d(P,Q)
es igual a
CONICAS Y COORDENADAS POLARES

5. 10.1 SECCIONES CONICAS
Ecuación de la parábola:
Vértice trasladado a (h, k) En general, la forma estándar de la ecuación de una
parábola con vértice (h, k) está dada por
CONICAS Y COORDENADAS POLARES

6. 10.1 SECCIONES CONICAS
Ecuación de la elipse:
CONICAS Y COORDENADAS POLARES

7. 10.1 SECCIONES CONICAS
Ecuación de la elipse:
Centro trasladado:
CONICAS Y COORDENADAS POLARES

8. 10.1 SECCIONES CONICAS
Ecuación de la hipérbola:
Centro en (0,0) y focos en eje x Centro en (0,0) y focos en eje x Centro en (0,0) y focos en eje y
CONICAS Y COORDENADAS POLARES

9. 10.1 SECCIONES CONICAS
Ecuación de la hipérbola:
Asíntotas: Toda hipérbola posee un par de asíntotas inclinadas que pasan por su
centro. Estas asíntotas son indicativas del comportamiento final, y como tales son
una ayuda invaluable en el trazado de la gráfica de una hipérbola.
CONICAS Y COORDENADAS POLARES

10. 10.2 ECUACIONES PARAMETRICAS
Parametrización de curvas rectangulares: Una curva C descrita por una función
continua y f (x) también se parametriza dejando x = t. Las ecuaciones paramétricas
para C son entonces
CONICAS Y COORDENADAS POLARES

11. 10.3 CALCULO Y ECUACIONES PARAMETRICAS
Si y' = dy/dx es una función diferenciable de t, se deduce que
CONICAS Y COORDENADAS POLARES

12. 10.3 CALCULO Y ECUACIONES PARAMETRICAS
CONICAS Y COORDENADAS POLARES

13. 10.4 SISTEMA DE COORDENADAS POLARES
Para establecer un sistema de coordenadas polares empleamos un sistema de
círculos centrados en un punto O, denominado polo, y líneas rectas o rayos que
emanen de O. Tomamos como eje de referencia una media línea horizontal dirigida
hacia la derecha del polo, a la cual se le nombra eje polar. Para especificar una
distancia r dirigida (con signo) desde O y un ángulo Θ cuyo lado inicial es el eje
polar y cuyo lado final es el rayo OP, se identifica el punto P mediante (r, Θ).
CONICAS Y COORDENADAS POLARES

14. 10.4 SISTEMA DE COORDENADAS POLARES
CONICAS Y COORDENADAS POLARES

15. 10.4 SISTEMA DE COORDENADAS POLARES
Conversión de coordenadas polares en rectangulares: Al sobreponer un sistema
de coordenadas rectangulares sobre un sistema de coordenadas polares, como se
muestra en la Figura, podemos convertir la descripción polar de un punto en
coordenadas rectangulares utilizando
x = r cos Θ y = r sen Θ
CONICAS Y COORDENADAS POLARES

16. 10.5 GRAFICA DE ECUACIONES POLARES
Círculos centrados en el origen: En general, si a es cualquier constante distinta de
cero, la gráfica polar de
Recta que pasa por el origen:
CONICAS Y COORDENADAS POLARES

17. 10.6 CALCULO EN COORDENADAS POLARES
Área de una región:
CONICAS Y COORDENADAS POLARES

18. 10.6 CALCULO EN COORDENADAS POLARES
Construcción de una integral: Suponga que r=f(Θ) es una función continua no
negativa sobre el intervalo [α,ß] donde 0<=α<=ß<=2π. Para encontrar el área A de
la región que se muestra en la Figura que está acotada por la gráfica de f y los
rayos Θ = α y Θ = ß, se empieza formando una partición P de [α,ß]:
CONICAS Y COORDENADAS POLARES