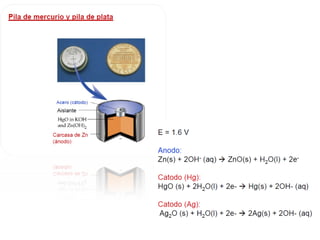
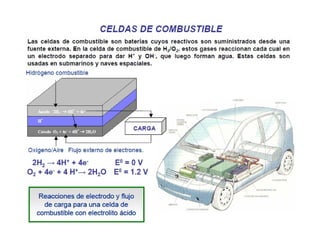
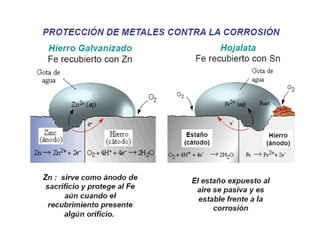
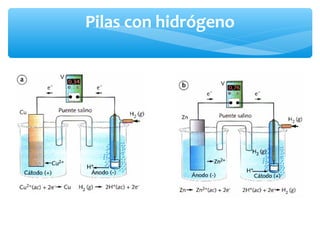
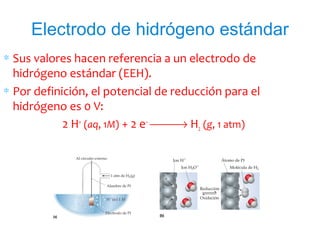
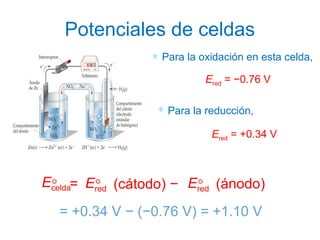
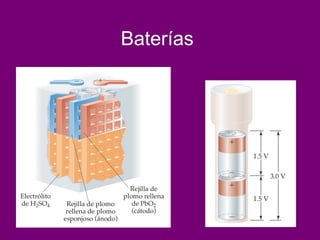
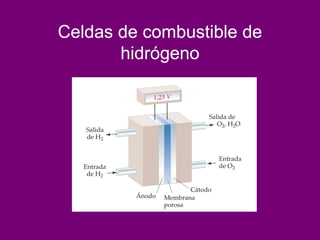
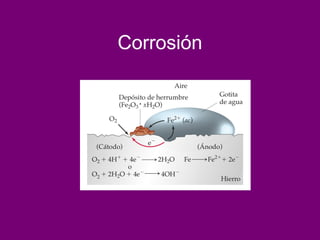
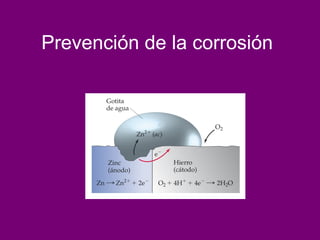
El documento describe conceptos clave de las reacciones redox como estado de oxidación, oxidación y reducción, y equilibrio redox. Explica el funcionamiento de baterías como la pila Daniell y pilas comerciales. También cubre electrólisis, fuerza electromotriz, potenciales de reducción estándar, ecuación de Nernst y ecuación de Faraday.

1. ELECTROQUIMICA
REACCIONES REDOX
PLAN ELECTIVO QUIMICA NM4
30 DE JULIO
Contenidos :
1. Estado de oxidación.
2. Oxidación – Reducción
3. Equilibrio de reacciones redox .

2. OBJETIVOS
Explicar la composición y el funcionamiento de las
baterías de uso
común.
Aplicar la variación de potencial estándar de electrodo
mediante la utilización de la tabla de potenciales.

3. Tipos de reacciones redox
(según su espontaneidad).

5. En las reacciones de oxidación-
reducción (redox) espontáneas,
los electrones se transfieren y la
energía se libera.
Podemos utilizar esta energía
para que trabaje si hacemos que
los electrones fluyan a través de
un dispositivo externo.

6. Pila Daniell.
∗ Consta de dos semiceldas
∗ Una con un electrodo de Cu en una disolución de CuSO4
∗ Otra con un electrodo de Zn
en una disolución de ZnSO4.
PILAS VOLTAICAS /PILAS VOLTAICAS /
CELDAS GALVÁNICASCELDAS GALVÁNICAS
∗ La pila anterior se representaría:
Ánodo Puente salino Cátodo
∗ Zn (s)  ZnSO4 (aq)  CuSO4 (aq)  Cu (s)
∗ Ánodo se lleva a cabo la oxidación:
∗ Zn – 2 e –
→ Zn2+
.
∗ Cátodo se lleva a cabo la reducción:
∗ Cu2+
+ 2 e –
→ Cu.

7. 7
Pilas comerciales.
Alcalina De mercurio (botón)Salina

16. Electrólisis
∗ Cuando la reacción redox no es espontánea en un sentido, podrá suceder
si desde el exterior se suministran los electrones.

18. Comparación de la polaridad de los electrodos en
pilas y electrólisis.

19. Fuerza electromotriz (fem)
• El flujo de electrones desde el
ánodo hacia el cátodo
es espontáneo en una pila.
• Los electrones fluyen desde el
punto de mayor hacia el de menor
potencial eléctrico.
Diferencia de potencial (ΔE) o Fuerza electromotriz (FEM): es la diferencia de
potencial eléctrico por unidad de carga, y se mide en Volts(V).
Un voltio es la diferencia de potencial eléctrico necesaria para impartir un joule de
energía a una carga de un coulomb:
1 V = 1 J
C

20. Potenciales
de reducción
estándar
Se han medido y
tabulado los
potenciales de
reducción para
muchos electrodos.

21. Pilas con hidrógeno

22. Electrodo de hidrógeno estándar
∗ Sus valores hacen referencia a un electrodo de
hidrógeno estándar (EEH).
∗ Por definición, el potencial de reducción para el
hidrógeno es 0 V:
2 H+
(aq, 1M) + 2 e−
→ H2 (g, 1 atm)

23. Se puede encontrar el potencial de celda en condiciones
estándares a través de esta ecuación:
Potenciales de celdas estándar
Ecelda° = Ered (cátodo) − Ered (ánodo)° °
Ya que el potencial de celda se basa
en la energía potencial por unidad de
carga, esta es una propiedad
intensiva.

24. Potenciales de celdas
∗ Para la oxidación en esta celda,
∗ Para la reducción,
Ered = −0.76 V°
Ered = +0.34 V°
Ecelda° = Ered° (cátodo) − Ered° (ánodo)
= +0.34 V − (−0.76 V) = +1.10 V

25. 25
Ejemplo:
Decir si será espontánea la siguiente reacción redox:
Cl2(g) + 2 I–
(aq)→ 2Cl–
(aq) + I2 (s)
∗ La reacción dada es la suma de las siguientes semirreacciones:
∗ RedRed. (cátodo):. (cátodo): Cl2(g) + 2e–
→ 2Cl–
(aq)
∗ Oxid.Oxid. (ánodo):(ánodo): 2 I–
(aq) → I2 (s) + 2e–
∗ Para que la reacción sea espontánea tiene que cumplirse que ∆
Epila > 0:
∗ ∆ Epila= Ecatodo– Eánodo= +1’36 V – 0’54 V = +0’72 V > 0
∗ luego es espontáneaespontánea (las moléculas de Cl2 tienen más tendencia a
reducirse que las de I2).

26. 26
Ejercicio :
Una pila consta de un electrodo de Mg introducido en una
disolución 1 M de Mg(NO3)2 y un electrodo de Ag en una
disolución 1 M de AgNO3 . ¿Qué electrodo actuará de cátodo
y de ánodo y cuál será el voltaje de la pila correspondiente?
∗ ¿Qué especie se reduce?¿Qué especie se reduce?
∗ La que tenga mayor potencial de reducción. En
este caso la Ag (+0,80 V) frente a los –2,37 V del
Mg.
∗ RedRed. (cátodo):. (cátodo): Ag+
(aq) + 1e–
→ Ag(s)
∗ Oxid.Oxid. (ánodo):(ánodo): Mg(s) → Mg2+
(aq) + 2e–
∗ ∆Epila= Ecatodo– Eánodo= +0,80 V – (–2,37 V)
∆∆EEpilapila = 3,17 V= 3,17 V

27. Electrochemistry
Se puede encontrar ∆G para una reacción redox
usando la ecuación:
∆G = −nFE
donde n ese número de moles de electrones
transferidos, y F es una constante, el Faraday.
1 F = 96,485 C/mol = 96,485 J/V-mol
Energía libre

28. Electrochemistry
Con base en los potenciales estándar de reducción de la tabla,
calcule el cambio de energía
libre estándar, ΔG°, de la reacción siguiente:
4Ag(s) + O2(g) + 4H+
(ac)↔4Ag+(ac) + 2H2O(l)

29. Electrochemistry
2Ag(s) + 12O2(g) + 2H+(ac) ↔ 2Ag+(ac) + H2O(l)

30. Electrochemistry
3Ni2+(
ac) + 2Cr(OH)3(s) + 10OH-
(ac)↔3Ni(s) + 2CrO4
2-
(ac) + 8H2O(l)

31. Energía libre
Bajo condiciones estándar,
∆G° = −nFE°

32. Ecuación de Nernst
• Recuerda que:
∆G = ∆G° + RT ln Q
• Esto significa:
−nFE = −nFE° + RT ln Q

33. Ecuación de Nernst
Al dividir ambas partes por −nF,
obtenemos la ecuación de Nernst:
E = E° −
RT
nF
ln Q
o, al usar logaritmos de base 10,
E = E° −
2.303 RT
nF
ln Q

34. Ecuación de Nernst
A temperatura ambiente (298 K),
por lo tanto la ecuación se convierte en:
E = E° −
0.0592
n
ln Q
2.303 RT
F
= 0.0592 V

35. 35
Electrólisis. Ecuación de Faraday.Electrólisis. Ecuación de Faraday.
La carga de un electrón es de 1’6 x 10–19
C y la
de 1 mol de electrones (6’02 x 1023
) es el
producto de ambos números: 96500 C = 1 F.
Con un mol de electrones se es capaz de
reducir 1 mol de metal monovalente o ½ mol
de metal divalente, es decir, un equivalente
del metal (Mat/valencia).
1 equivalente precisa 96500 C
neq (m (g)/Meq) precisarán Q

36. 36
Ecuación de Faraday (cont.).Ecuación de Faraday (cont.).
De la proporción anterior se deduce:
m Q
neq = —— = —————
Meq 96500 C/eq
De donde, sustituyendo Q por I · t (más
fáciles de medir) y despejando “m” se
obtiene:
× × × ×
= =
×-
( )
96500 º 96500
eq at
M I t M I t
m g
n e

37. 37
Ejercicio F:Ejercicio F: Una corriente de 4 amperiosUna corriente de 4 amperios
circula durante 1 hora y 10 minutos a través de doscircula durante 1 hora y 10 minutos a través de dos
células electrolíticas que contienen, respectivamente, sulfato decélulas electrolíticas que contienen, respectivamente, sulfato de
cobre (II) y cloruro de aluminio,cobre (II) y cloruro de aluminio, a)a) Escriba las reacciones queEscriba las reacciones que
se producen en el cátodo de ambas células electrolíticas.se producen en el cátodo de ambas células electrolíticas.
b)b) Calcule los gramos de cobre y aluminio metálicos que seCalcule los gramos de cobre y aluminio metálicos que se
habrán depositado. Datos: Masas atómicas: Cu = 63,5 y Al =habrán depositado. Datos: Masas atómicas: Cu = 63,5 y Al =
27,0. Constante de Faraday : F = 96500 C·eq27,0. Constante de Faraday : F = 96500 C·eq-1-1
a)a) Cu2+
+ 2 e–
→ Cu ; Al3+
+ 3 e–
→ Al
b)b) Meq · I · t (63,5/2) g/eq·4 A· 4200 s
m (Cu) = ————— = ——————————— = 5,53 g5,53 g
96500 C/eq 96500 C/eq
Meq · I · t (27,0/3) g/eq·4 A· 4200 s
m (Al) = ————— = ——————————— = 1,57 g1,57 g
96500 C/eq 96500 C/eq
Problema
Selectividad
(Junio 98)
Problema
Selectividad
(Junio 98)

38. 38
Ejemplo:Ejemplo: Se realiza la electrólisis de unSe realiza la electrólisis de un
disolución de tricloruro de hierro, haciendo pasardisolución de tricloruro de hierro, haciendo pasar
una corriente de 10 A durante 3 horas. Calcula launa corriente de 10 A durante 3 horas. Calcula la
cantidad de hierro depositado en el cátodo.cantidad de hierro depositado en el cátodo.
El tricloruro en disolución estará disociado:
FeCl3 → 3 Cl–
+ Fe3+
La reducción será: Fe3+
+ 3 e–
→ Fe
Meq x I x t (55,8/3) g/eq x 10 A x 3 x 3600 s
m (g) = ————— = —————————————
96500 C/eq 96500 C/eq
m (g) =m (g) = 20,82 g20,82 g

39. Aplicaciones de las
reacciones de
oxidación-reducción

40. Baterías

41. Batería alcalina

42. Celdas de combustible de
hidrógeno

43. Corrosión

44. Prevención de la corrosión

45. Electrólisis

46. 46
Comparación de la polaridad de losComparación de la polaridad de los
electrodos en pilas y electrólisis.electrodos en pilas y electrólisis.
© ECIR. Química 2º Bachillerato