Subido porL2DJ Temas de Matemáticas Inc.
Graficas rosas
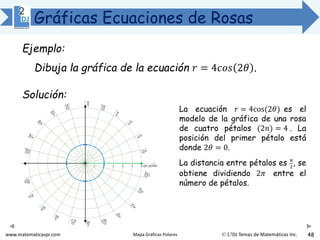
El documento describe las ecuaciones y gráficas de rosas polares de n pétalos y 2n pétalos. Explica que una rosa de n pétalos tiene una ecuación de la forma r = asen nθ o r = acos nθ, donde el ángulo entre pétalos es 2π/n y cada pétalo mide a unidades. Para una rosa de 2n pétalos, la ecuación y posición de los pétalos se define de manera similar.
Más contenido relacionado
Más de L2DJ Temas de Matemáticas Inc.
Graficas rosas
- 1. www.matematicaspr.com © L2DJTemas de Matemáticas Inc. Coordenadas Polares, Vectores y Números Complejos • Gráficas Rosas 1
- 2. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar. Gráficas Ecuaciones de Rosas 46
- 3. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas La gráfica de la izquierda es una rosa de tres pétalos. 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 4. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 5. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 6. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 7. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 8. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 9. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 El ángulo entre los pétalos es 2𝜋 dividido por el número de pétalos (𝑛). 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 10. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 El ángulo entre los pétalos es 2𝜋 dividido por el número de pétalos (𝑛) y cada uno mide 𝑎 unidades. 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 𝑎, 0 𝑎, 2𝜋 3 −𝑎, 𝜋 3 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 11. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 El ángulo entre los pétalos es 2𝜋 dividido por el número de pétalos (𝑛) y cada uno mide 𝑎 unidades. 46 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 𝑎, 0 𝑎, 2𝜋 3 −𝑎, 𝜋 3 𝑎, 𝜋 6 𝑎, 5𝜋 6 −𝑎, 𝜋 2 Rosas de 𝑛 pétalos Es una rosa de 𝑛 pétalos de longitud 𝑎, si 𝑛 es impar.
- 12. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Gráficas Ecuaciones de Rosas 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Rosas de 2𝑛 pétalos
- 13. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares La gráfica de la izquierda es una rosa de cuatro pétalos. Gráficas Ecuaciones de Rosas 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 14. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 15. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 16. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 17. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 18. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 19. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 La distancia entre los pétalos es 2𝜋 entre el número de pétalos (2𝑛). 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 20. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 𝑎, 𝜋 −𝑎, 𝜋 2 𝑎, 0 −𝑎, 3𝜋 2 La distancia entre los pétalos es 2𝜋 entre el número de pétalos (2𝑛) y cada uno mide 𝑎 unidades. Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 21. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Ecuación polar 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 donde, 𝑎 > 0 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 donde, 𝑎 > 0 Gráficas Ecuaciones de Rosas Posición del primer pétalo Ecuación 𝑟 = 𝑎𝑠𝑒𝑛 𝑛𝜃 dividir 𝜋 2 por 𝑛 Ecuación 𝑟 = 𝑎𝑐𝑜𝑠 𝑛𝜃 dividir 0 por 𝑛 47 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 𝑎, 𝜋 −𝑎, 𝜋 2 𝑎, 0 −𝑎, 3𝜋 2 La distancia entre los pétalos es 2𝜋 entre el número de pétalos (2𝑛) y cada uno mide 𝑎 unidades. 𝑎, 5𝜋 4 −𝑎, 7𝜋 4 𝑎, 𝜋 4 −𝑎, 3𝜋 4 Es una rosa de 2𝑛 pétalos de longitud 𝑎, si 𝑛 es par. Rosas de 2𝑛 pétalos
- 22. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 23. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Solución: La ecuación 𝑟 = 4cos(2𝜃) es el modelo de la gráfica de una rosa de cuatro pétalos (2𝑛) = 4 . La posición del primer pétalo está donde 2𝜃 = 0. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 24. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Solución: La ecuación 𝑟 = 4cos(2𝜃) es el modelo de la gráfica de una rosa de cuatro pétalos (2𝑛) = 4 . La posición del primer pétalo está donde 2𝜃 = 0. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 25. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Solución: La ecuación 𝑟 = 4cos(2𝜃) es el modelo de la gráfica de una rosa de cuatro pétalos (2𝑛) = 4 . La posición del primer pétalo está donde 2𝜃 = 0. La distancia entre pétalos es 𝜋 2 , se obtiene dividiendo 2𝜋 entre el número de pétalos. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 26. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Solución: La ecuación 𝑟 = 4cos(2𝜃) es el modelo de la gráfica de una rosa de cuatro pétalos (2𝑛) = 4 . La posición del primer pétalo está donde 2𝜃 = 0. La distancia entre pétalos es 𝜋 2 , se obtiene dividiendo 2𝜋 entre el número de pétalos. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 27. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 48 Solución: La ecuación 𝑟 = 4cos(2𝜃) es el modelo de la gráfica de una rosa de cuatro pétalos (2𝑛) = 4 . La posición del primer pétalo está donde 2𝜃 = 0. La distancia entre pétalos es 𝜋 2 , se obtiene dividiendo 2𝜋 entre el número de pétalos. Dibujar la rosa con pétalos de 4 unidades de largo. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 −4, 3𝜋 2 −4, 𝜋 2 4,04, 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 4𝑐𝑜𝑠 2𝜃 .
- 28. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 29. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Solución: La ecuación 𝑟 = 5sen(3𝜃)es el modelo de la gráfica de una rosa de tres pétalos 𝑛 = 3. La posición del primer pétalo está donde 3𝜃 = 𝜋 2 . 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 30. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Solución: La ecuación 𝑟 = 5sen(3𝜃)es el modelo de la gráfica de una rosa de tres pétalos 𝑛 = 3. La posición del primer pétalo está donde 3𝜃 = 𝜋 2 . 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 31. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Solución: La distancia entre pétalos es 2𝜋 3 , se obtiene dividiendo 2𝜋 entre el número de pétalos. La ecuación 𝑟 = 5sen(3𝜃)es el modelo de la gráfica de una rosa de tres pétalos 𝑛 = 3. La posición del primer pétalo está donde 3𝜃 = 𝜋 2 . 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 32. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Solución: 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 La distancia entre pétalos es 2𝜋 3 , se obtiene dividiendo 2𝜋 entre el número de pétalos. La ecuación 𝑟 = 5sen(3𝜃)es el modelo de la gráfica de una rosa de tres pétalos 𝑛 = 3. La posición del primer pétalo está donde 3𝜃 = 𝜋 2 . Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 33. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 49 Solución: Dibujar la rosa con pétalos de 5 unidades de largo. 1 2 3 4 5 6 eje polar 𝜋 2 3𝜋 2 𝜋 La distancia entre pétalos es 2𝜋 3 , se obtiene dividiendo 2𝜋 entre el número de pétalos. La ecuación 𝑟 = 5sen(3𝜃)es el modelo de la gráfica de una rosa de tres pétalos 𝑛 = 3. La posición del primer pétalo está donde 3𝜃 = 𝜋 2 .5, 𝜋 6 5, 5𝜋 6 5, 3𝜋 2 Ejemplo: Dibuja la gráfica de la ecuación 𝑟 = 5𝑠𝑒𝑛 3𝜃 .
- 34. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares PrácticaBuscar el Manual de Práctica Hacer los ejercicios de la página 6 50
- 35. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas Práctica: Graficar las siguientes ecuaciones polares. 1. 𝑟 = 6𝑐𝑜𝑠 5𝜃 2. 𝑟 = 4𝑠𝑒𝑛 2𝜃 51 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋
- 36. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 51 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋 Rosa de 5 pétalos de longitud 6. Primer pétalo en 0 y cada uno a 2𝜋 5 . 6,0 6, 6𝜋 5 6, 4𝜋 5 6, 8𝜋 5 6, 2𝜋 5 Práctica: Graficar las siguientes ecuaciones polares. 1. 𝑟 = 6𝑐𝑜𝑠 5𝜃 2. 𝑟 = 4𝑠𝑒𝑛 2𝜃
- 37. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Gráficas Ecuaciones de Rosas 51 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋 1 2 3 4 5 6eje polar 𝜋 2 3𝜋 2 𝜋 Rosa de 5 pétalos de longitud 6. Primer pétalo en 0 y cada uno a 2𝜋 5 . 6,0 6, 6𝜋 5 6, 4𝜋 5 6, 8𝜋 5 6, 2𝜋 5 Rosa de 4 pétalos de longitud 4. Primer pétalo en 𝜋 4 y cada uno a 𝜋 2 . 4, 𝜋 4 4, 5𝜋 4 −4, 7𝜋 4 −4, 3𝜋 4 Práctica: Graficar las siguientes ecuaciones polares. 1. 𝑟 = 6𝑐𝑜𝑠 5𝜃 2. 𝑟 = 4𝑠𝑒𝑛 2𝜃
- 38. www.matematicaspr.com © L2DJTemas de Matemáticas Inc.Mapa Gráficas Polares Mapa Gráficas Polares 57 Simetría de las Gráficas Polares •Polo •Eje Polar •Recta 𝜃 = 𝜋 2 Gráficas Rectas •Recta inclinada •Recta Paralela al Eje Polar •Recta Paralela a 𝜃 = 𝜋 2 Gráficas Círculos •Circulo con centro en el polo •Circulo con centro en el eje polar •Circulo con centro en la recta 𝜃 = 𝜋 2 Gráficas Caracoles • Cardiode • Caracol con Lazo • Caracol sin Lazo Gráficas Rosas • Rosas de N Pétalos • Rosas de 2N Pétalos • Gráfica Lemniscata • Gráfica de Espiral Gráficas de Ecuaciones Polares