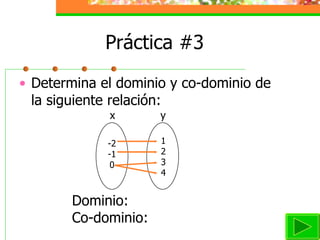
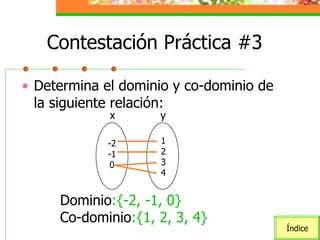
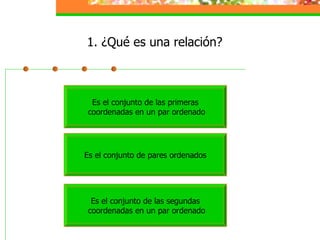
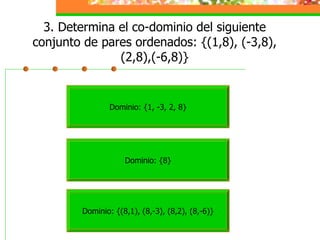
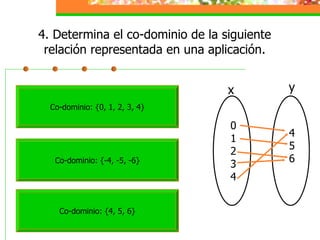
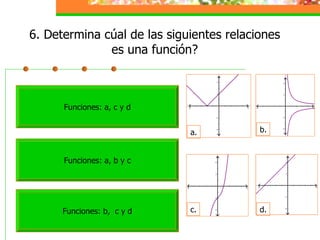
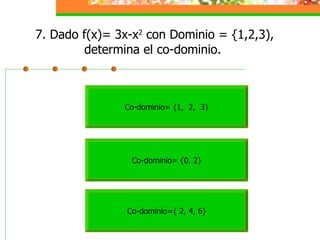
Este módulo instruccional trata sobre relaciones y funciones. Introduce el tema, objetivos de aprendizaje, y una lista de contenidos que incluye definiciones de relaciones, funciones, dominio y co-dominio, y ejemplos. También incluye actividades de práctica y una autoevaluación.

1. Módulo Instruccional Relaciones y Funciones Comenzar Guía para el maestro

4. Índice 1. Repasemos 2. Relaciones 3. Relación Inversa 4. Dominio y Co-dominio 5. Funciones 6. Autoevaluación Referencias

8. Formas de representar una relación (4,4) (-1,3) (0,-5) Pares ordenados Hay varias formas de representar una relación: con pares ordenados, en tabla, en una gráfica o en una aplicación. Tablas Gráficas x y 4 -1 0 4 3 -5 Aplicación x y 4 -1 0 4 3 -5

18. Ejemplos de Funciones y No Funciones a. {(2,4), (3,1), (5,2), (-1,-2)} Es función . Dado que para cada valor de x hay un único valor de y . O sea, los valores de x NO se repiten. 0 -3 2 3 4 2 -4 b. Es función . Dado que para cada valor de x hay un único valor de y . O sea, los valores de x NO se repiten. No importa que dos elementos del dominio estén relacionados con un mismo elemento del co-dominio. c. 2 2 -3 3 2 4 2 -4 x y y x NO es función . Dado que en esta relación para el elemento 2 del dominio existen dos elementos en el co-dominio. O sea, los valores de x SI se repiten.

21. Funciones x f(x) Dominio Co-Dominio a b c d f(a) f(b) f(c) f(d) Nota: al Co-dominio también se le conoce como alcance, rango, recorrido o amplitud

26. Dado f(x)= 5x-7 con Dominio = {1,2,3), determina el co-dominio. Determinar dominio de una función x f(x)= 5x-7 (x,y) 1 2 3 5 . 1 – 7=-2 (1,-2) 5 . 2 – 7=3 5 . 3 – 7=8 (2,3) (3,8) Co-dominio= {-2, 3, 8}

27. Práctica #5 Dado g(x) = con Dominio= {0,1,2}, determina el co-dominio. Dado h(x) = determina el dominio.

28. Contestación Práctica #5 Dado g(x) = con Dominio= {0,1,2}, determina el co-dominio. Dado h(x) = determina el dominio. x (x,y) 0 1 2 Dado que dentro del radical no odemos tener un negativo los valores de x ≥ 3 y x ≤ -3 Dominio= {x| x ≥ 3 ó x ≤ -3 } Co-dominio = { , , 1} Índice

29. Prueba de autoevaluación Índice Comienza la prueba

30. 1. ¿Qué es una relación? Es el conjunto de las primeras coordenadas en un par ordenado Es el conjunto de pares ordenados Es el conjunto de las segundas coordenadas en un par ordenado

31. 2. Selecciona la aseveración correcta. Toda función es una relación. En ocasiones una función es una relación. Toda relación es un función.

32. 3. Determina el co-dominio del siguiente conjunto de pares ordenados: {(1,8), (-3,8), (2,8),(-6,8)} Dominio: {1, -3, 2, 8} Dominio: {(8,1), (8,-3), (8,2), (8,-6)} Dominio: {8}

33. 4. Determina el co-dominio de la siguiente relación representada en una aplicación. Co-dominio: {0, 1, 2, 3, 4} Co-dominio: {4, 5, 6} Co-dominio: {-4, -5, -6} x y 0 1 2 3 4 4 5 6

34. 5. ¿Cuál de las siguientes representaciones es una función? Funciones: a y b Funciones: a y c Funciones: b y c x y 0 1 2 3 5 6 7 7 {(1,4), (2,4), (3,4)} a. b. c.

35. 6. Determina cúal de las siguientes relaciones es una función? Funciones: a, c y d Funciones: b, c y d Funciones: a, b y c a. b. c. d.

36. 7. Dado f(x)= 3x-x 2 con Dominio = {1,2,3), determina el co-dominio. Co-dominio= {1, 2, 3} Co-dominio={ 2, 4, 6} Co-dominio= {0, 2}

37. 8. Determina el dominio de la siguiente función: Dominio = {todos los números reales) Dominio = {todo número real excepto 0} Dominio = {todo número real excepto 2}

38. 9. Determina el dominio de la siguiente función: Dominio = {todos los números reales) Dominio = {todo número real excepto x=-3} Dominio = {todo número real excepto x=3}

39. 10. Determina el dominio de la siguiente función: Dominio = {todos los números reales) Dominio = {todo número real excepto x=0 y x=9} Dominio = {todo número real excepto x=0 y x=-9}

40. 11. Determina el dominio de la siguiente función: Dominio = {x: x= 3) Dominio = {x: x 3} Dominio = {x: x 3}

41. 12. Determina el dominio de la siguiente función: Dominio = {x|x € R} Dominio = {x| x ≠ 2} y x ≠ -3} Dominio = {x| x ≠ -2 y x ≠ 3}

42. Resultados de autoevaluación Índice Resultados de la prueba

43. Referencias Brown, R.G., Dolciani, M.P., Sorgenfrey, R.H., Kane, R.B. (2000). Algebra and Trigonometry . Illinois: Houghton Mifflin Company, pp. 141-165. Collins, W., Cuevas, G., Foster, A.G., Gordon, B., Moore-Harris, B., Rath, J., et. al. (1998). Algebra 1 . Ohio: The McGraw Hill Companies, pp. 252-321. Estado Libre Asociado de Puerto Rico, Departamento de Educación (2008). Guía Operacional: Funciones y Modelos . Puerto Rico: Autor. Estado Libre Asociado de Puerto Rico, Departamento de Educación (2007). Estándares de Contenido y Expectativas por Grado: Programa de Matemáticas . Puerto Rico: Autor. Índice

44. Descripción del módulo Este módulo contiene material relacionado al tema de Relaciones y Funciones . El estudiante trabajará con los siguientes conceptos: relación, relación inversa, función, dominio, co-dominio. Incluye definiciones, ejemplos y ejercicios de práctica. Además, contiene una prueba de autoevaluación a ser contestada por el estudiante. El módulo está preparado para ser utilizado por los estudiantes de nivel superior en el curso de Funciones y Modelos. Corresponde particularmente a: Unidad 1: Funciones y Transformaciones Expectativa A.PR.11.2.1: Determina el dominio y el alcance de las funciones a partir de sus diferentes representaciones Destreza: Hallar el dominio y el recorrido de una función, partiendo de su gráfica y otras representaciones según establece el Mapa Curricular del curso.

45. Población y Duración El módulo podrá ser utilizado por los estudiantes del curso básico y avanzado de Funciones y Modelos que se ofrece en el nivel escolar superior requeridos en el sistema de educación pública en Puerto Rico. La duración del módulo será de aproximadamente tres días. El módulo se ofrecerá durante la discusión del tema Relaciones y Funciones .

46. Recursos y Manejo del módulo El módulo se trabajará utilizando las computadoras disponibles en la escuela. El módulo será custodiado por el maestro, quien se encargará de distribuirlo en las computadoras del laboratorio móvil de la escuela. El maestro del curso será el encargado de supervisar y dar seguimiento al estudiante durante su utilización.