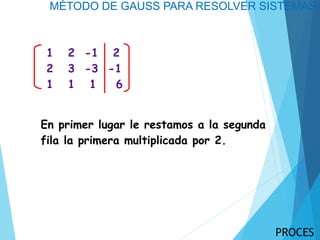
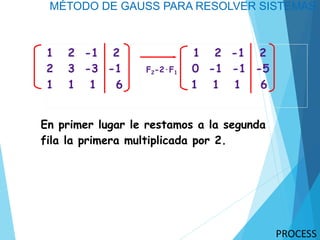
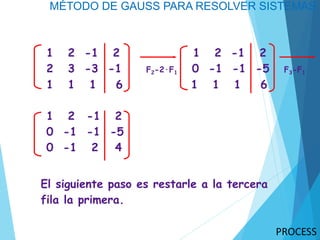
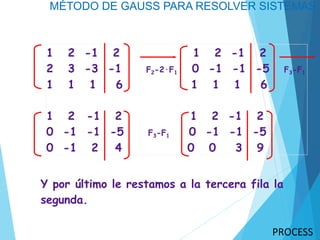
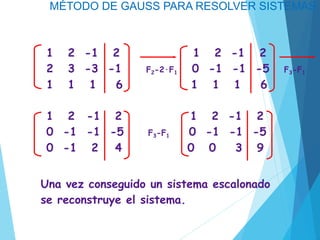
El método de Gauss para resolver sistemas de ecuaciones lineales involucra transformar la matriz aumentada del sistema en una forma escalonada a través de operaciones elementales de filas, y luego resolver el sistema escalonado comenzando con la ecuación con menos incógnitas. Se demuestra el método resolviendo un sistema de 3 ecuaciones y 3 incógnitas.

1. Método De Gauss ParaMétodo De Gauss Para
Resolver Sistemas DeResolver Sistemas De
Ecuaciones LinealesEcuaciones Lineales

2. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Para utilizar el método de Gauss se realizan
unas transformaciones en las filas de esa
matriz hasta que conseguimos que los
elementos por debajo de la diagonal principal
sean todos nulos.

3. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Las transformaciones permitidas son las
siguientes:
1) Se pueden cambiar entre sí dos filas.
2) Se pueden multiplicar o dividir por un
número distinto de cero todos los elementos de
una fila.
3) A una fila se le puede sumar otra
multiplicada por un número.

4. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Vamos a ver el método con un ejemplo
concreto.
Queremos resolver el sistema siguiente:
x + 2y - z = 2
2 x + 3y – 3z = -1
x + y + z = 6

5. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Vamos a ver el método con un ejemplo
concreto.
Queremos resolver el sistema siguiente:
x + 2y - z = 2
2 x + 3y – 3z = -1
x + y + z = 6
Lo primero es escribir el sistema mediante
la matriz ampliada.

6. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
1 2 -1 2
2 3 -3 -1
1 1 1 6
En primer lugar le restamos a la segunda
fila la primera multiplicada por 2.
PROCES

7. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
1 2 -1 2 1 2 -1 2
2 3 -3 -1 F2-2·F1 0 -1 -1 -5
1 1 1 6 1 1 1 6
En primer lugar le restamos a la segunda
fila la primera multiplicada por 2.

8. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
1 2 -1 2 1 2 -1 2
2 3 -3 -1 F2-2·F1 0 -1 -1 -5 F3-F1
1 1 1 6 1 1 1 6
1 2 -1 2
0 -1 -1 -5
0 -1 2 4
El siguiente paso es restarle a la tercera
fila la primera.

9. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
1 2 -1 2 1 2 -1 2
2 3 -3 -1 F2-2·F1 0 -1 -1 -5 F3-F1
1 1 1 6 1 1 1 6
1 2 -1 2 1 2 -1 2
0 -1 -1 -5 F3-F1 0 -1 -1 -5
0 -1 2 4 0 0 3 9
Y por último le restamos a la tercera fila la
segunda.

10. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
1 2 -1 2 1 2 -1 2
2 3 -3 -1 F2-2·F1 0 -1 -1 -5 F3-F1
1 1 1 6 1 1 1 6
1 2 -1 2 1 2 -1 2
0 -1 -1 -5 F3-F1 0 -1 -1 -5
0 -1 2 4 0 0 3 9
Una vez conseguido un sistema escalonado
se reconstruye el sistema.

11. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Una vez conseguido un sistema escalonado se
reconstruye el sistema y se resuelve comenzando
por la ecuación con menos incógnitas.
x + 2y - z = 2
- y - z = -5
3z = 9

12. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Una vez conseguido un sistema escalonado se
reconstruye el sistema y se resuelve comenzando
por la ecuación con menos incógnitas.
x + 2y - z = 2
- y - z = -5
3z = 9 z = 3
PROCES

13. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Una vez conseguido un sistema escalonado se
reconstruye el sistema y se resuelve comenzando
por la ecuación con menos incógnitas.
x + 2y - z = 2
- y - z = -5 y = 5-z = 2
3z = 9 z = 3
PROCES

14. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Una vez conseguido un sistema escalonado se
reconstruye el sistema y se resuelve comenzando
por la ecuación con menos incógnitas.
x + 2y - z = 2 x = 2-2y+z = 1
- y - z = -5 y = 5-z = 2
3z = 9 z = 3
PROCES

15. MÉTODO DE GAUSS PARA RESOLVER SISTEMAS
Una vez conseguido un sistema escalonado se
reconstruye el sistema y se resuelve comenzando
por la ecuación con menos incógnitas.
x + 2y - z = 2 x = 2-2y+z = 1
- y - z = -5 y = 5-z = 2
3z = 9 z = 3
La solución es, por tanto: x=1, y=2, z=3.