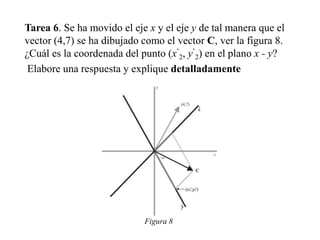
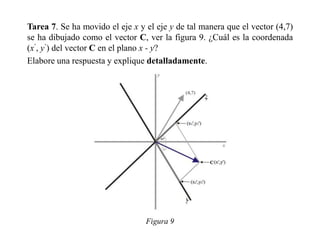
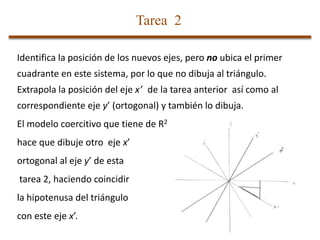
La tesis presenta el diseño de una secuencia didáctica para el estudio de las transformaciones lineales en R2. La secuencia consiste en 7 tareas con figuras geométricas que buscan que los estudiantes construyan un modelo mental sobre cómo las transformaciones lineales cambian la forma de los objetos al mover los ejes del plano cartesiano. La secuencia fue aplicada a 5 estudiantes, analizando sus respuestas para evaluar si el diseño ayudó a comprender mejor las transformaciones lineales.

1. CENTRO DE INVESTIGACIÓN EN CIENCIA APLICADA
Y TECNOLOGÍA AVANZADA
CICATA-IPN
P R E S E N TA C I Ó N D E L A T E S I S
Diseño de una secuencia didáctica para el
estudio de la Transformación Lineal en R2
Trabajo que presenta
Héctor Hernández Guzmán
Directores de tesis
M.C. Juan Gabriel Molina Zavaleta
Dr. Alejandro Miguel Rosas Mendoza
México, D. F. octubre de 2013

2. En este trabajo se plantea el diseño de una secuencia
didáctica para el estudio, en alumnos de nivel
superior, del concepto de Transformación Lineal (TL)
en R2,
y que se estudia en la materia de
Álgebra Lineal,
idea que nace ante la dificultad en estudiantes
para aceptar la existencia de ciertas
transformaciones lineales en contexto geométrico.

3. Creemos que algunas de esas dificultades que los
estudiantes enfrentan se deben a la influencia de
modelos tácitos intuitivos presentes en ellos,
por lo que este trabajo se basa en la
Teoría de los modelos intuitivos de Fischbein (1989),
quien considera que los modelos que crean
los estudiantes son, casi siempre, representaciones
imperfectas de los conceptos modelados.

4. Las consideraciones teóricas en que fundamentamos
nuestro trabajo se centran en aspectos
tácitos del conocimiento
es decir
los modelos tácitos.

5. En relación a la intuición, Fischbein señala que su papel
es el de crear una apariencia de certeza
sobre las interpretaciones o representaciones, y
considera que la intuición o conocimiento intuitivo es
un tipo de cognición, el cual se acepta de forma
inmediata por ser evidente, confiriéndole un carácter de
certeza intrínseca.

6. Respecto al tema de la transformación lineal esta es
una clase especial de función, definida como T:U U
sobre el conjunto R misma que cumple con las
siguientes dos propiedades
1. T (u v) T (u) T (v),
2. T (cu) cT (u),
u, v en el dominio de T
u y todos los escalares c

7. En esta presentación planteamos lo que se
hizo, cómo se hizo y qué se logró al aplicar a cinco
estudiantes una secuencia sobre la TL.
e identificar si el diseño de la misma conduce a los
estudiante a adquirir un conocimiento sobre la TL en
función de sus modelos tácitos.

8. Para esta investigación, se consideró un resultado del
trabajo de Molina (2004) donde se concluyó que los
estudiantes entrevistados no reconocieron la
transformación lineal de corte.

9. Por lo anterior, nos planteamos la tarea de diseñar una
secuencia cuyo propósito didáctico es que el estudiante
construya un modelo
que incluya más características de la TL en R2,
es decir, que no sólo considere
expansiones, contracciones, rotaciones y las
combinaciones de éstas.
Este modelo lo concebimos bajo dos formas explícitas:

10. 1
La transformación en R2 como el
cambio de forma
de objetos representados en el plano, generado
como consecuencia de
mover los ejes x y y del
plano cartesiano

11. 2
La transformación en R2 como un
modelo algebraico
que representa el cambio de forma de los objetos en
R2 debido al movimiento de los ejes.
El modelo algebraico es el siguiente:

12. El análisis a priori de las
dos actividades propuestas
para la secuencia didáctica
se desarrollaron
conforme
a lo siguiente:

13. Actividad 1
Para que el estudiante construya tal conocimiento
proponemos involucrarlo en la realización de cuatro
tareas (ver secuencia didáctica), éstos son
problemas matemáticos que involucran
figuras geométricas en R2.
Las tareas están pensadas desde la teoría de la intuición
de Fischbein (1987, 1989),
por lo siguiente:

14. Asumimos que algunas representaciones observables
que se pueden manipular, favorecen la percepción de
ideas intuitivas. Por lo anterior, un
modelo explícito
como una figura, es un objeto concreto (observable),
y partimos del supuesto de que puede ser
manipulado mentalmente.

15. Actividad 2
Para que el estudiante construya dicho modelo
algebraico proponemos involucrarlo en la realización
de tres tareas (ver secuencia didáctica).
Las tareas están íntimamente relacionadas porque
cada solución de ellas es
una de las etapas
para determinar el modelo en cuestión.

16. En esta segunda actividad estamos considerando
que el alumno ya ha construido un
modelo mental
sobre la TL, el cual se generó durante el
desarrollo de la actividad 1.

17. SECUENCIA DIDÁCTICA
EL diseño de la secuencia consta de
siete tareas
en las cuales a partir de la observación de ciertos
dibujos o modelos explícitos
se les pide a los estudiantes una respuesta
detallada en relación a la explicación dada, y
se muestran a continuación:

18. Tarea 1. Observe el triángulo de la figura 1:
Figura 1

19. Si se mueve el eje x y el eje y como en la figura 2, ¿cómo
queda dibujado el triángulo?
Elabore una respuesta y explique detalladamente.
Figura 2

20. Tarea 2. Si se mueve el eje x y el eje y como en la figura
3, ¿cómo queda dibujado el triángulo de la figura 1? Elabore
una respuesta y explique detalladamente.
Figura 3

21. Tarea 3. Si se mueve el eje y como en la figura 4, ¿cómo
quedaría dibujado el triángulo de la figura 1 (nota: el eje x'
queda en el mismo lugar que el eje x)?
Elabore una respuesta y explique detalladamente.
Figura 4

22. Tarea 4. Observe el vector de la figura 5:
Figura 5

23. Si se mueve el eje x y el eje y como en la figura
6, ¿cómo queda dibujado el vector?
Elabore una respuesta y explique detalladamente.
Figura 6

24. Tarea 5. Se ha movido el eje x y el eje y de tal manera que el
vector (4,7) se ha dibujado como el vector C, ver la figura 7.
¿Cuál es la coordenada del punto (x’1, y’1) en el plano x - y?
Elabore una respuesta y explique detalladamente.
Figura 7

25. Tarea 6. Se ha movido el eje x y el eje y de tal manera que el
vector (4,7) se ha dibujado como el vector C, ver la figura 8.
¿Cuál es la coordenada del punto (x’2, y’2) en el plano x - y?
Elabore una respuesta y explique detalladamente
Figura 8

26. Tarea 7. Se ha movido el eje x y el eje y de tal manera que el vector (4,7)
se ha dibujado como el vector C, ver la figura 9. ¿Cuál es la coordenada
(x’, y’) del vector C en el plano x - y?
Elabore una respuesta y explique detalladamente.
Figura 9

27. PUESTA EN ESCENA
Se seleccionaron cinco alumnos de la carrera de
Ingeniería Industrial del Tecnológico de Estudios
Superiores de Cuautitlán Izcalli (TESCI).
Los estudiantes contaron para la solución de la
secuencia con hojas blancas y bolígrafos.
El no darles lápices a los estudiantes fue para que no
borraran lo hecho conservándose las evidencias de
los intentos en la solución de las tareas.

28. Para trabajar, cada uno de los
estudiantes ocupó una mesa
donde se dispuso para su uso
de hojas blancas y bolígrafos.

29. El profesor proporcionó a cada
estudiante la primera tarea a
resolver, y posteriormente
les explica en qué consiste
ésta.
Nosotros consideramos que no era forzoso que
respondieran correctamente la actividad, pues
queríamos observar cómo respondían los
estudiantes la secuencia.

30. Antes que los estudiantes resolvieran la secuencia
se les comentó que podían hacer preguntas, mismas
que serían contestadas por el profesor, en el sentido
de clarificar el contenido de la pregunta, pero no la
forma de resolverla.
Como ninguno de los estudiantes preguntó, no se
efectuó dicha intervención.
La no intervención del profesor, fue un hecho
intencional, se deseaba constatar hasta dónde
podían responder los estudiantes la secuencia
solos, para examinar las interpretaciones que ellos
hacían de los modelos explícitos.

31. Para ejemplificar los resultados
presentamos de manera particular lo
realizado por el estudiante Andrés.

32. Tarea 1
Andrés identificó tanto el plano cartesiano como
el triángulo rectángulo,
intuye que el triángulo
gira junto con los
ejes coordenados
manteniéndose
los catetos del triángulo
paralelos a los nuevos ejes

33. Tarea 2
Identifica la posición de los nuevos ejes, pero no ubica el primer
cuadrante en este sistema, por lo que no dibuja al triángulo.
Extrapola la posición del eje x’ de la tarea anterior así como al
correspondiente eje y’ (ortogonal) y también lo dibuja.
El modelo coercitivo que tiene de R2
hace que dibuje otro eje x’
ortogonal al eje y’ de esta
tarea 2, haciendo coincidir
la hipotenusa del triángulo
con este eje x’.

34. Tarea 3
Identifica la posición de los nuevos ejes x’- y’. Se ve que
extrapola el modelo mental generado en las tareas
anteriores y dibuja otro eje y ortogonal al original y’.
Aunque confunde los ejes,
extrapola la idea de que la
hipotenusa del triángulo
está sobre un eje coordenado x’.

35. Tarea 4
El nuevo modelo explícito (un vector) influye en él pues no logra
ubicarlo en el nuevo sistema coordenado x’- y’. Considera que el
lado opuesto de x’ es x, y el de y’ es y. Luego intuye que estos ejes
son como los originales, por lo que,
si el vector mostrado esta entre
el eje x y el eje y, también
lo estará entre sus nuevos
ejes x, y.
Para ubicarlo gradúa a los ejes
y así lo posiciona en lugar que
considera es el correcto

36. Tarea 5
Extrapola la idea de cómo se posiciona un vector
de la tarea anterior y de
inmediato ubica al
vector (4,7)
haciendo
graduaciones en los ejes del sistema original x – y.
Luego, en otro dibujo termina de dibuja el modelo
explicito de la tarea 5.

37. Como su modelo mental se basa en los ejes coordenados también
dibuja al ángulo de 45 fijando así al eje x’, por lo que solo mueve
(o gira) al eje y’. No logra ubicar al vector C.
Basándose en la posición que guarda
el vector C con el eje x intuye
se nueva posición y lo dibuja.
Su modelo mental no contempla al
punto ni a sus coordenadas (x’1,y’1) por
lo que no las calcula. Se aprecia una reflexión.

38. Tarea 6
Extrapola lo hecho en la tarea anterior y agrega un nuevo
dato el ángulo de 60 , y considera que ambos ejes
x’ y y’ quedan fijos.
Asigna los valores del vector (4,7)
a los ejes primos correspondientes.
Pensamos que ya esta presente el
punto (x’2,y’2) en su modelo y lo
calcula dando para x’2 el valor
de – 4 (tal vez considerando que
la distancia a medir parte de C
hacia y’1 por lo que le cambia el signo).

39. Tarea 7
Igual que en las dos tareas anteriores dibuja el modelo
explícito de la tarea. Extrapola la idea de la tarea
anterior de cómo obtuvo el punto (-4,7)
y asigna las coordenada (4,-7) al
punto (x’2,y’2). Finalmente
resuelve la tarea y asigna las
coordenadas (-4,-7) al vector C.

40. A continuación se presenta un análisis de
la puesta en escena de la secuencia
didáctica,
considerando cada una de las las tareas
resueltas por los estudiantes.

41. Tarea 1
Los modelos explícitos de la figura 1 son entendidos
por los estudiantes pues se aprecia que han
identificado que el ángulo recto está en ambos
modelos (figuras 1 y 2) y que los catetos son
paralelos
a los ejes coordenados. Identifican el movimiento
de los ejes junto con el triángulo como un
giro, manteniéndose la perpendicularidad de R2.

42. Tarea 2
Los estudiantes identifican que los ejes se
movieron. No todos dibujan al triángulo y quienes
lo hacen lo presentan sin
deformarlo
pues aparentemente no hay nada que les haga
suponer que cambia de forma.
Otra razón puede ser que un rasgo del modelo
mental que tienen del triangulo no les permite
deformarlo.

43. Tarea 3
Se aprecia que los estudiantes intuyen que los
ejes se mueven, pero no cómo lo hacen, por lo
que no identifican la posición correcta del
triángulo, y aunque lo dibujan
tampoco lo deforman
Pensamos que el modelo mental que ellos tienen
del triángulo es el de una figura que
no se deforma
coaccionando su respuesta implícitamente.

44. Tarea 4
Se ve que los estudiantes identifican al nuevo
modelo explícito (vector) pero no pueden
manipularlo conjuntamente con R2
Se aprecia que tratan de ubicar al vector en
función de cómo sus modelos mentales intuyen el
movimiento de los ejes por lo que
no lo ubican en la posición correcta.
Es posible también que el modelo explícito
al no proporcionarles la dirección de
éste, tampoco puedan determinar su sentido.

45. Tarea 5
Los estudiantes identifican al vector (4,7) en el
plano x - y, se aprecia que no han construido un
modelo mental de la forma en que giran los
ejes, por lo que no pueden determinar la dirección
del vector respecto al nuevo sistema coordenado.
Posiblemente el modelo explícito de la figura 5
coaccione las respuestas de lo estudiantes pues
todos ellos no calcularon las coordenadas del
punto (x1’,y1’)
que se les piden, y proceden a calcular las
coordenadas de punto (x’,y’)en función del único
dato numérico en el modelo, el vector (4,7).

46. Tarea 6
Los estudiantes extrapolan la solución que dieron
en la tarea anterior y proceden a calcular las
componentes de C en función del par ordenado
(4,7)
Posiblemente un modelo mental generado en las
dos tareas anteriores coaccione sus
respuestas, pues igual que en la tarea anterior la
mayoría de los estudiantes no calcularon las
coordenadas del punto (x2’,y2’)

47. Tarea 7
Tratan de posicionar al vector C, sin hacer
cálculos, pues no consiguieron determinar
correctamente las coordenadas de los puntos
(x’1,y’1) y (x’2,y’2)
Los estudiantes extrapolan la idea generada en
las dos tareas anteriores y tratan de obtener las
componentes del vector C definidas por
(x’,y’), nuevamente en función del único dato
numérico que es el vector (4,7).

48. Al observar lo realizado por los estudiantes notamos que
ellos se enfocan en
encontrar el vector C.
Puede ser error del modelo explícito mostrado a los
estudiantes, pues en el dibujo resalta el vector C
mientras que los puntos que se desean encontrar no
resaltan. Entonces implícitamente le estamos diciendo al
estudiante que "lo importante es el vector C".

49. CONCLUSIONES
En la solución de esta secuencia emergen ideas
intuitivas que se convierte en un obstáculo para que
el estudiante resuelva adecuadamente tareas
posteriores, como la perpendicularidad entre ejes o
el mismo triángulo rectángulo,
pues no es sencillo que los estudiantes perciban que
una figura se tiene que deformar.
Posiblemente se requiera un conocimiento previo
para que lleguen a la conclusión de que el triángulo
también cambia de forma.

50. Otra situación que se pudo haber presentado en la
tareas 1 es que los estudiantes la resolvieron por ser
simple o intuitiva, y se pudo haber convertido en
una técnica que al extrapolarla les impidió resolver
las siguientes tareas.
Lo anterior surge porque la solución de la tarea 1
implica que los ejes se pueden mover y el triángulo
junto con ellos, pero sin deformarse éste último.

51. Algunos modelos explícitos usados resaltaron, sin
darnos cuenta, elementos que alteraron el orden
deseado en la solución de las tareas, e incluso la
interpretación de la misma.
Por lo anterior, es conveniente que los modelos
explícitos empleados contribuyan implícitamente a
la solución de una tarea específica a resolver.

52. Situaciones como la anterior podrían solventarse si
se hace presente la
participación del profesor con la intención de que
los modelos de los estudiantes se vean
coaccionados o motivados por su influencia al
resolverse la secuencia.

53. Al usar un modelo explícito para comunicar
alguna idea,
implícitamente
le podemos estar comunicando otra a los
estudiantes, lo que pudo ser un obstáculo en la
solución
de la secuencia didáctica.

54. Por ejemplo, en la expresión “Plano x – y”
el modelo algebraico pudo haber
coaccionado sus respuestas,
al interpretar a éste como las coordenadas de un
punto en el cuarto cuadrante.

55. También debe de tenerse cuidado en la redacción
de las preguntas para separar la idea que se quiere
que manipulen los estudiantes.
En nuestro caso, aunque estamos planteando la idea
de movimiento, esta no implica necesariamente una
deformación o cambio de forma como nosotros lo
habíamos considerado.

56. Gracias por su atención
.