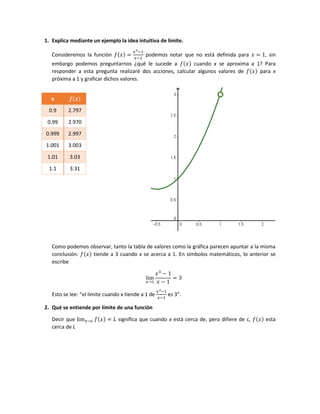
Este documento explica conceptos clave sobre límites de funciones. Define el límite de una función como el valor al que se aproxima la función cuando la variable independiente se acerca a un valor particular. Presenta un ejemplo numérico y gráfico para ilustrar esta idea intuitiva. También enlista propiedades importantes de límites como la suma, resta, multiplicación y división de funciones, así como límites de potencias y raíces. Finalmente, describe cuándo una función es continua en un intervalo abierto o cerrado.

1. Calculo Diferencial
MT-MCDI-1602-B2-001
TSU. Matemáticas
Unidad 2 – Representación de límites
Eduardo Castillo López
ES162001459
Octubre 17, 2016

2. 1. Explica mediante un ejemplo la idea intuitiva de límite.
Consideremos la función 𝑓(𝑥) =
𝑥3−1
𝑥−1
podemos notar que no está definida para 𝑥 = 1, sin
embargo podemos preguntarnos ¿qué le sucede a 𝑓(𝑥) cuando x se aproxima a 1? Para
responder a esta pregunta realizaré dos acciones, calcular algunos valores de 𝑓(𝑥) para x
próxima a 1 y graficar dichos valores.
Como podemos observar, tanto la tabla de valores como la gráfica parecen apuntar a la misma
conclusión: 𝑓(𝑥) tiende a 3 cuando x se acerca a 1. En símbolos matemáticos, lo anterior se
escribe
lim
𝑥→1
𝑥3
− 1
𝑥 − 1
= 3
Esto se lee: “el límite cuando x tiende a 1 de
𝑥3−1
𝑥−1
es 3”.
2. Qué se entiende por límite de una función
Decir que lim 𝑥→𝑐 𝑓(𝑥) = 𝐿 significa que cuando x está cerca de, pero difiere de c, 𝑓(𝑥) esta
cerca de L
x 𝒇(𝒙)
0.9 2.797
0.99 2.970
0.999 2.997
1.001 3.003
1.01 3.03
1.1 3.31

3. 3. Enuncia las propiedades de límites
Sea n un número positivo, k una constante, f y g funciones con límites en c. Entonces,
1.
Límite de una
constante
lim
𝑥→𝑐
𝑘 = 𝑘
2.
Límite de la función
identidad
lim
𝑥→𝑐
𝑥 = 𝑐
3.
Límite de una
constante
multiplicada por una
función
lim
𝑥→𝑐
𝑘𝑓(𝑥) = 𝑘 lim
𝑥→𝑐
𝑓(𝑥)
4.
Límite de una suma
de funciones
lim
𝑥→𝑐
[𝑓(𝑥) + 𝑔(𝑥)] = lim
𝑥→𝑐
𝑓(𝑥) + lim
𝑥→𝑐
𝑔(𝑥)
5.
Límite de una resta
de funciones
lim
𝑥→𝑐
[𝑓(𝑥) − 𝑔(𝑥)] = lim
𝑥→𝑐
𝑓(𝑥) − lim
𝑥→𝑐
𝑔(𝑥)
6.
Límite de una
multiplicación de
funciones
lim
𝑥→𝑐
[𝑓(𝑥) ∙ 𝑔(𝑥)] = lim
𝑥→𝑐
𝑓(𝑥) ∙ lim
𝑥→𝑐
𝑔(𝑥)
7.
Límite de una división
de funciones
lim
𝑥→𝑐
[
𝑓(𝑥)
𝑔(𝑥)
] =
lim
𝑥→𝑐
𝑓(𝑥)
lim
𝑥→𝑐
𝑔(𝑥)
, 𝑑𝑎𝑑𝑜 𝑞𝑢𝑒 lim
𝑥→𝑐
𝑔(𝑥) ≠ 0
8.
Límite de una
potencia
lim
𝑥→𝑐
[𝑓(𝑥)] 𝑛
= [lim
𝑥→𝑐
𝑓(𝑥)]
𝑛
9. Límite de una raíz
lim 𝑥→𝑐 √𝑓(𝑥)
𝑛
= √lim 𝑥→𝑐 𝑓(𝑥)
𝑛
, 𝑑𝑎𝑑𝑜 𝑞𝑢𝑒 lim 𝑥→𝑐 𝑓(𝑥) > 0
cuando n es par.
10.
Si f es una función polinomial o una función racional, entonces
lim
𝑥→𝑐
𝑓(𝑥) = 𝑓(𝑐)
siempre que el valor del denominador para c no sea cero, en el caso de una función
racional.

4. 11.
Sean f, g y h funciones que satisfacen 𝑓(𝑥) ≤ 𝑔(𝑥) ≤ ℎ(𝑥) para toda x próxima a c, con la
posible excepción de c. Si
lim
𝑥→𝑐
𝑓(𝑥) = lim
𝑥→𝑐
ℎ(𝑥) = 𝐿, 𝑒𝑛𝑡𝑜𝑛𝑐𝑒𝑠 lim
𝑥→𝑐
𝑔(𝑥) = 𝐿
4. Describa cuando existe continuidad y discontinuidad de una función en un intervalo abierto
o cerrado
Decimos que f es continua en un intervalo abierto (𝑎, 𝑏) si es continua para todo punto de
(𝑎, 𝑏).
Es continua en el intervalo cerrado [𝑎, 𝑏] si es continua en (𝑎, 𝑏), continua a la derecha de a y a
la izquierda de b.