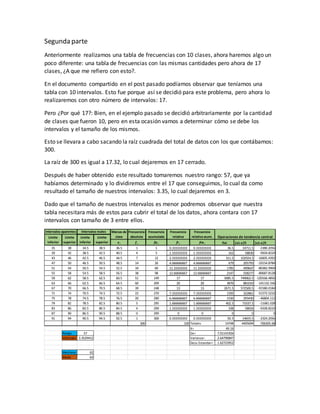
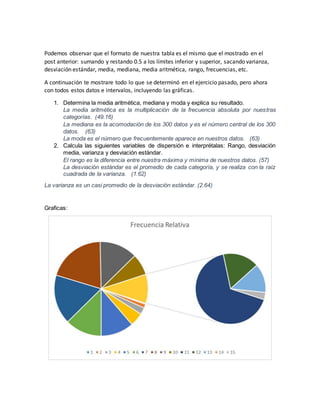
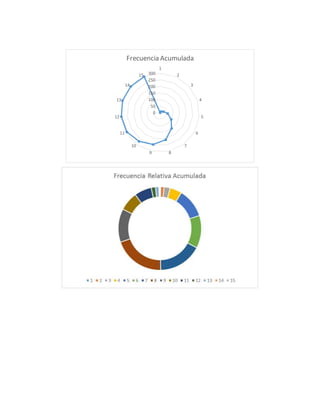
Este documento describe cómo crear una tabla de frecuencias con 17 intervalos en lugar de 10 para los mismos 300 datos. Explica que la raíz cuadrada de 300 datos es 17, por lo que habrá 17 intervalos. El rango de los datos (57) se divide entre 17 para obtener un tamaño de intervalo de 3. Luego calcula medidas de tendencia central como la media, mediana y moda de los datos agrupados en la nueva tabla de 17 intervalos.

1. Universidad Tecnológica de Torreón
Estadística: Datos agrupados: Ejercicio #5 2da Parte
Procesos Industriales Área Manufactura
Fernando Dominguez Borrego
2°A

2. Segunda parte
Anteriormente realizamos una tabla de frecuencias con 10 clases, ahora haremos algo un
poco diferente: una tabla de frecuencias con las mismas cantidades pero ahora de 17
clases, ¿A que me refiero con esto?.
En el documento compartido en el post pasado podíamos observar que teníamos una
tabla con 10 intervalos. Esto fue porque así se decidió para este problema, pero ahora lo
realizaremos con otro número de intervalos: 17.
Pero ¿Por qué 17?: Bien, en el ejemplo pasado se decidió arbitrariamente por la cantidad
de clases que fueron 10, pero en esta ocasión vamos a determinar cómo se debe los
intervalos y el tamaño de los mismos.
Esto se llevara a cabo sacando la raíz cuadrada del total de datos con los que contábamos:
300.
La raíz de 300 es igual a 17.32, lo cual dejaremos en 17 cerrado.
Después de haber obtenido este resultado tomaremos nuestro rango: 57, que ya
habíamos determinado y lo dividiremos entre el 17 que conseguimos, lo cual da como
resultado el tamaño de nuestros intervalos: 3.35, lo cual dejaremos en 3.
Dado que el tamaño de nuestros intervalos es menor podremos observar que nuestra
tabla necesitara más de estos para cubrir el total de los datos, ahora contara con 17
intervalos con tamaño de 3 entre ellos.
xi f i fai fri frai fixi |x1-x|fi |x1-x|fi
35 38 34.5 38.5 36.5 1 1 0.333333333 0.333333333 36.5 14711.5 -2380.2056
39 42 38.5 42.5 40.5 4 5 1.333333333 1.333333333 162 58830 -9504.8224
43 46 42.5 46.5 44.5 7 12 2.333333333 2.333333333 311.5 102924.5 -16605.4392
47 50 46.5 50.5 48.5 14 26 4.666666667 4.666666667 679 205793 -33154.8784
51 54 50.5 54.5 52.5 34 60 11.33333333 11.33333333 1785 499647 -80382.9904
55 58 54.5 58.5 56.5 38 98 12.66666667 12.66666667 2147 558277 -89687.8128
59 62 58.5 62.5 60.5 51 149 17 17 3085.5 749062.5 -120166.4856
63 66 62.5 66.5 64.5 60 209 20 20 3870 881010 -141132.336
67 70 66.5 70.5 68.5 39 248 13 13 2671.5 572500.5 -91580.0184
71 74 70.5 74.5 72.5 22 270 7.333333333 7.333333333 1595 322861 -51572.5232
75 78 74.5 78.5 76.5 20 290 6.666666667 6.666666667 1530 293430 -46804.112
79 82 78.5 82.5 80.5 5 295 1.666666667 1.666666667 402.5 73337.5 -11681.028
83 86 82.5 86.5 84.5 4 299 1.333333333 1.333333333 338 58654 -9328.8224
87 90 86.5 90.5 88.5 0 299 0 0 0 0 0
91 94 90.5 94.5 92.5 1 300 0.333333333 0.333333333 92.5 14655.5 -2324.2056
300 100 Totales 14748 4405694 -706305.68
X= 49.16
Rango 57 Dx= 7.01141926
Intervalo 3.3529412 Varianza= 2.64790847
Desv.Estandar= 1.62723952
Mediana 62
Moda 63
Operaciones de tendencia central
Frecuencia
acumulada
Frecuencia
relativa
Frecuencia
relativa acum.
Intervalos aparentes
Límite
inferior
Límite
superior
Marcas de
clase
Frecuencia
absolutaLimite
superior
Intervalos reales
Limite
inferior

3. Podemos observar que el formato de nuestra tabla es el mismo que el mostrado en el
post anterior: sumando y restando 0.5 a los límites inferior y superior, sacando varianza,
desviación estándar, media, mediana, media aritmética, rango, frecuencias, etc.
A continuación te mostrare todo lo que se determinó en el ejercicio pasado, pero ahora
con todos estos datos e intervalos, incluyendo las gráficas.
1. Determina la media aritmética, mediana y moda y explica su resultado.
La media aritmética es la multiplicación de la frecuencia absoluta por nuestras
categorías. (49.16)
La mediana es la acomodación de los 300 datos y es el número central de los 300
datos. (63)
La moda es el número que frecuentemente aparece en nuestros datos. (63)
2. Calcula las siguientes variables de dispersión e interprétalas: Rango, desviación
media, varianza y desviación estándar.
El rango es la diferencia entre nuestra máxima y mínima de nuestros datos. (57)
La desviación estándar es el promedio de cada categoría, y se realiza con la raíz
cuadrada de la varianza. (1.62)
La varianza es un casi promedio de la desviación estándar. (2.64)
Graficas:

4. 0
50
100
150
200
250
300
1
2
3
4
5
6
7
89
10
11
12
13
14
15
Frecuencia Acumulada