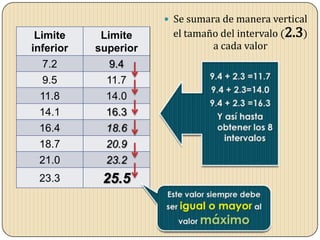
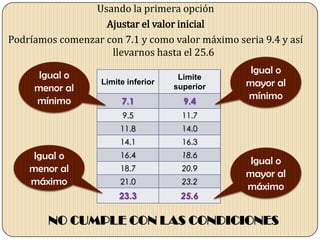
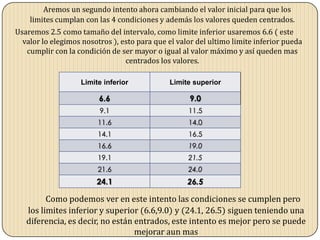
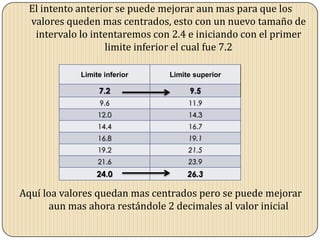
Este documento describe los pasos para agrupar datos en intervalos. Primero se identifican el valor máximo y mínimo de los datos. Luego se calcula el rango, número de intervalos y tamaño de cada intervalo. Se obtienen los límites inferiores y superiores, ajustándolos hasta que queden centrados y cumplan con las condiciones requeridas.

1. Carolina Zúñiga Rivera 3 B
Lic. Edgar Mata Ortiz

2.  Para poder resolver un problema de datos agrupados
primero se tiene que identificar el valor máximo y el
mínimo ,esto quiere decir que el máximo es la cifra
mas grande que hay dentro de todos los datos que yo
tenga y el mínimo es el valor mas pequeño.
 En este caso los valores son con un decimal:
Máximo =25.8
Mínimo =7.3

3.  Hay que obtener el rango que tendrán mis datos,
esto se hace restando el valor máximo al mínimo y
así obtendremos este valor.
Máximo – Mínimo
25.8 – 7.3 = 18.5
 Lo siguiente es obtener el numero de intervalos esto se
puede obtener de una operación o puede ser
arbitrario, esto quiere decir que nos proporcionan o
nosotros decidimos el valor que le queremos dar, en
este caso se nos proporciono el número de intervalos
el cual fue 8

4.  Lo siguiente es obtener el tamaño del intervalo, esto se
hace dividiendo el rango entre el numero de intervalos.
Rango / Numero de intervalos
18.5 / 8 = 2.3125 TAMAÑO DEL INTERVALO
 En este paso lo que se hace es redondear el TAMAÑO
DEL INTERVALO se redondea según los decimales que
se van a manejar en el caso de este problema es a un
decimal, entonces quedaría de la siguiente manera
TAMAÑO DEL INTERVALO = 2.3

5.  Ahora debemos obtener los
intervalos aparentes, lo primero
que se tiene que hacer es
determinar el limite inferior,
recordando que mi valor mínimo
es 7.3
Limite
inferior
7.2
9.5
Lo siguiente que debemos hacer
es sumarle al primer limite
inferior el valor del tamaño del
intervalo redondeado en forma
vertical como se muestra a
continuación.
Limite
inferior
7.2
9.5
11.8
14.1
16.4
18.7
21.0
23.3

6. Limite inferior
7.2
9.5
11.8
14.1
16.4
18.7
21.0
23.3
Al obtener todos los intervalos (recordemos que deben ser 8)
asegurarnos que las condiciones se cumplan para proseguir a
sacar el limite superior.

7.  Ahora obtendremos los limites superiores.
Limite
inferior
Limite
superior
7.2 9.4
9.5
11.8
14.1
16.4
18.7
21.0
23.3

8.  Se sumara de manera vertical
el tamaño del intervalo (2.3)
a cada valor
Limite
inferior
Limite
superior
7.2 9.4
9.5 11.7
11.8 14.0
14.1 16.3
16.4 18.6
18.7 20.9
21.0 23.2
23.3 25.5

9.  Al tener ambos limites (inferior y superior) ahora debemos
checar que las 4 condiciones se cumplan
Limite
inferior
Limite
superior
7.2 9.4
9.5 11.7
11.8 14.0
14.1 16.3
16.4 18.6
18.7 20.9
21.0 23.2
23.3 25.5
Igual o
mayor al
mínimo
Igual o
mayor al
máximo
Igual o
menor al
máximo
Igual o
menor al
mínimo
NO CUMPLE CON LAS CONDICIONES

10.  El primer intento no resulto así que
tenemos que hacer otro tenemos 3
opciones
1. Ajustar el valor inicial
2. Cambiar el tamaño del intervalo
3. Cambiar el numero de intervalos (es
muy raro que esto suceda)

11. Usando la primera opción
Ajustar el valor inicial
Podríamos comenzar con 7.1 y como valor máximo seria 9.4 y así
llevarnos hasta el 25.6
Limite inferior
Limite
superior
7.1 9.4
9.5 11.7
11.8 14.0
14.1 16.3
16.4 18.6
18.7 20.9
21.0 23.2
23.3 25.6
Igual o
mayor al
mínimo
Igual o
mayor al
máximo
Igual o
menor al
máximo
Igual o
menor al
mínimo
NO CUMPLE CON LAS CONDICIONES

12. Como podemos ver
en este caso se
cumplen las
condiciones pero los
valores no quedan
centrados es decir
hay diferencia de
decimales, estos
valores se podrían
utilizar pero también
podemos mejorarlos
cambiando el valor
inicial del primer
intento.
Limite inferior
Limite
superior
7.2 9.6
9.7 12.1
12.2 14.6
14.7 17.1
17.2 19.6
19.7 22.1
22.2 24.6
24.2 27.1
Usando la opción 2
Cambiar el tamaño de intervalo
Se podría cambiar el tamaño del intervalo a 2.4 o 2.5, probaremos
con 2.5
9.6-7.2 =2.4
27.1-24.2=2.9
Hay una
diferenci
a de 0.5
decimas

13. Aremos un segundo intento ahora cambiando el valor inicial para que los
limites cumplan con las 4 condiciones y además los valores queden centrados.
Usaremos 2.5 como tamaño del intervalo, como limite inferior usaremos 6.6 ( este
valor lo elegimos nosotros ), esto para que el valor del ultimo limite inferior pueda
cumplir con la condición de ser mayor o igual al valor máximo y así queden mas
centrados los valores.
Limite inferior Limite superior
6.6 9.0
9.1 11.5
11.6 14.0
14.1 16.5
16.6 19.0
19.1 21.5
21.6 24.0
24.1 26.5
Como podemos ver en este intento las condiciones se cumplen pero
los limites inferior y superior (6.6,9.0) y (24.1, 26.5) siguen teniendo una
diferencia, es decir, no están entrados, este intento es mejor pero se puede
mejorar aun mas

14. El intento anterior se puede mejorar aun mas para que los
valores queden mas centrados, esto con un nuevo tamaño de
intervalo lo intentaremos con 2.4 e iniciando con el primer
limite inferior el cual fue 7.2
Limite inferior Limite superior
7.2 9.5
9.6 11.9
12.0 14.3
14.4 16.7
16.8 19.1
19.2 21.5
21.6 23.9
24.0 26.3
Aquí loa valores quedan mas centrados pero se puede mejorar
aun mas ahora restándole 2 decimales al valor inicial

15. Limite inferior Limite superior
7.0 9.4
9.5 11.9
12.0 14.4
14.5 16.9
17.0 19.4
19.5 21.9
22.0 24.4
24.5 26.9
Como podemos ver en este caso los valores quedan centrados a la
perfección entre el limite inferior y el superior hay 2.4 de separación
en ambos extremos, es decir que no existe ninguna diferencia, así que
esta es una solución optima, estos son los valores que utilizaremos
para obtener los intervalos reales.
2.4
2.4