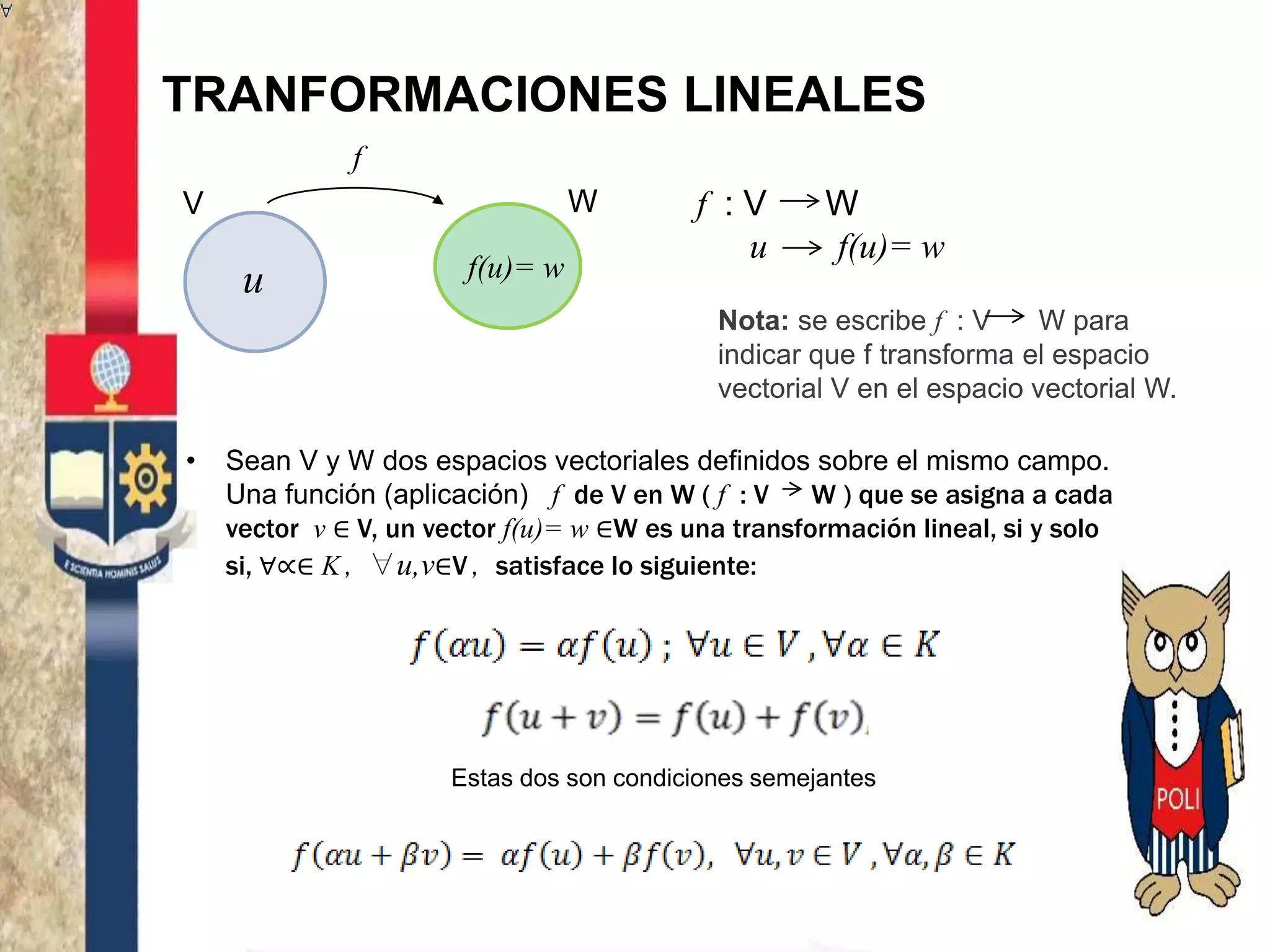
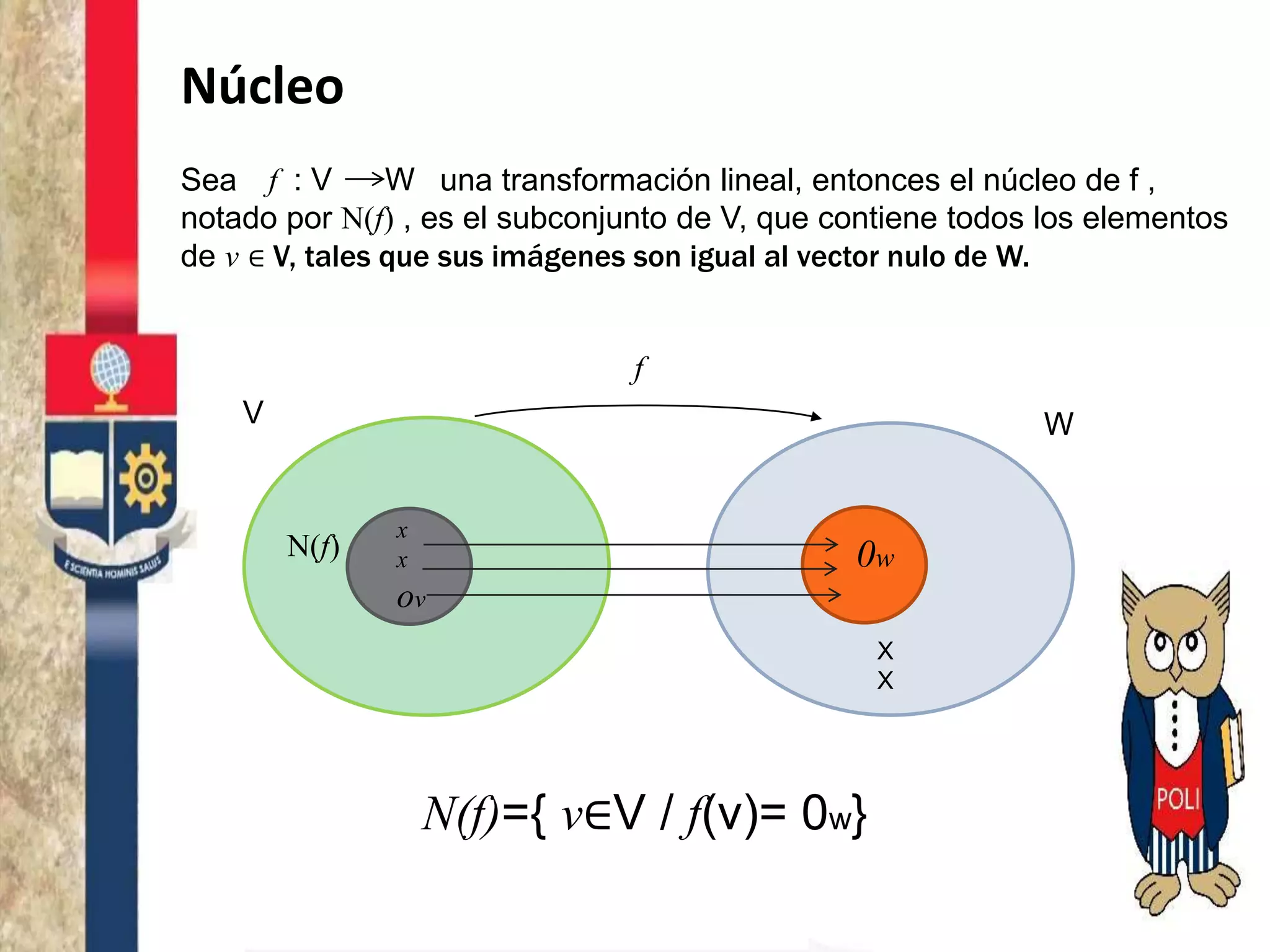
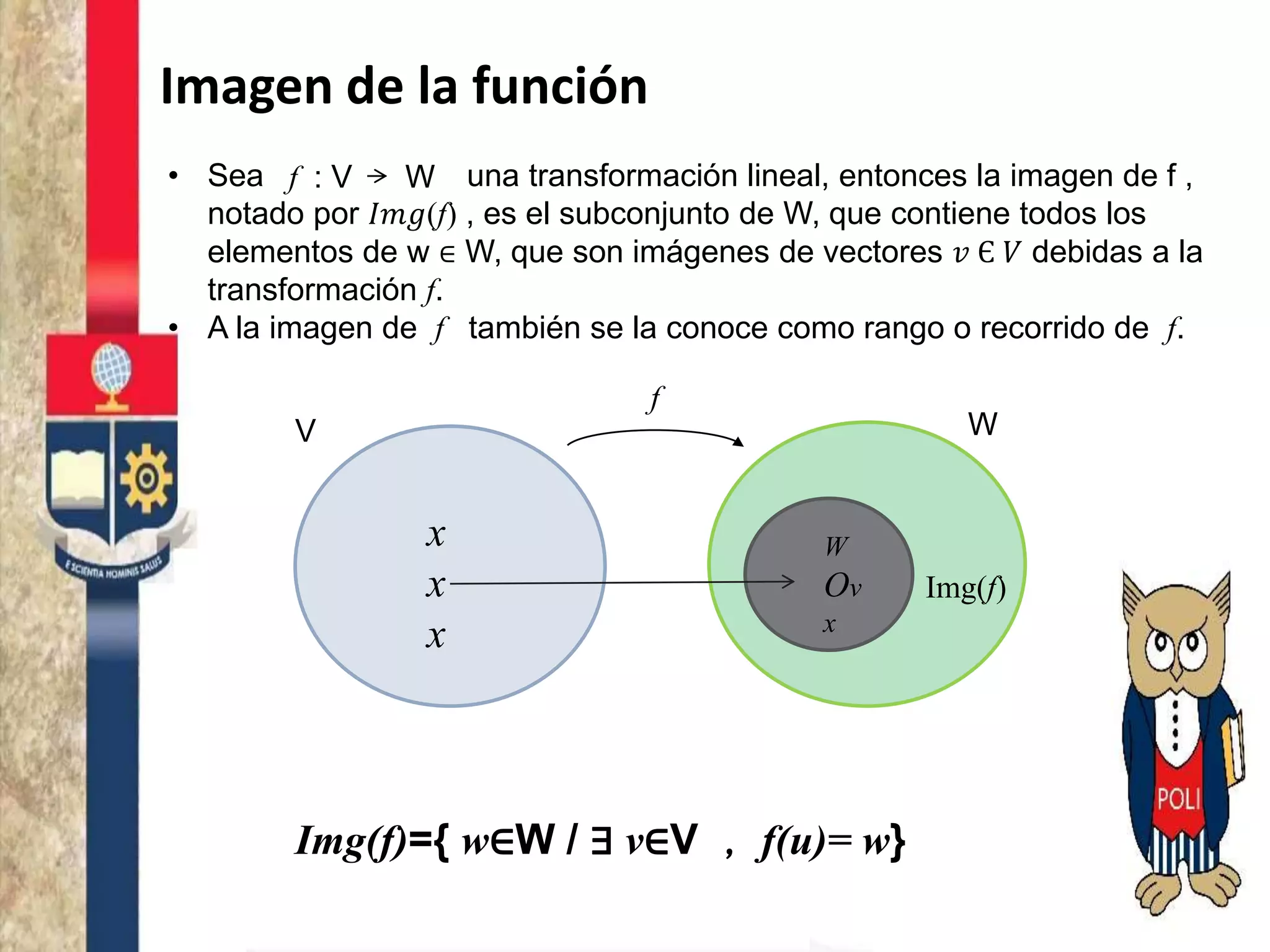
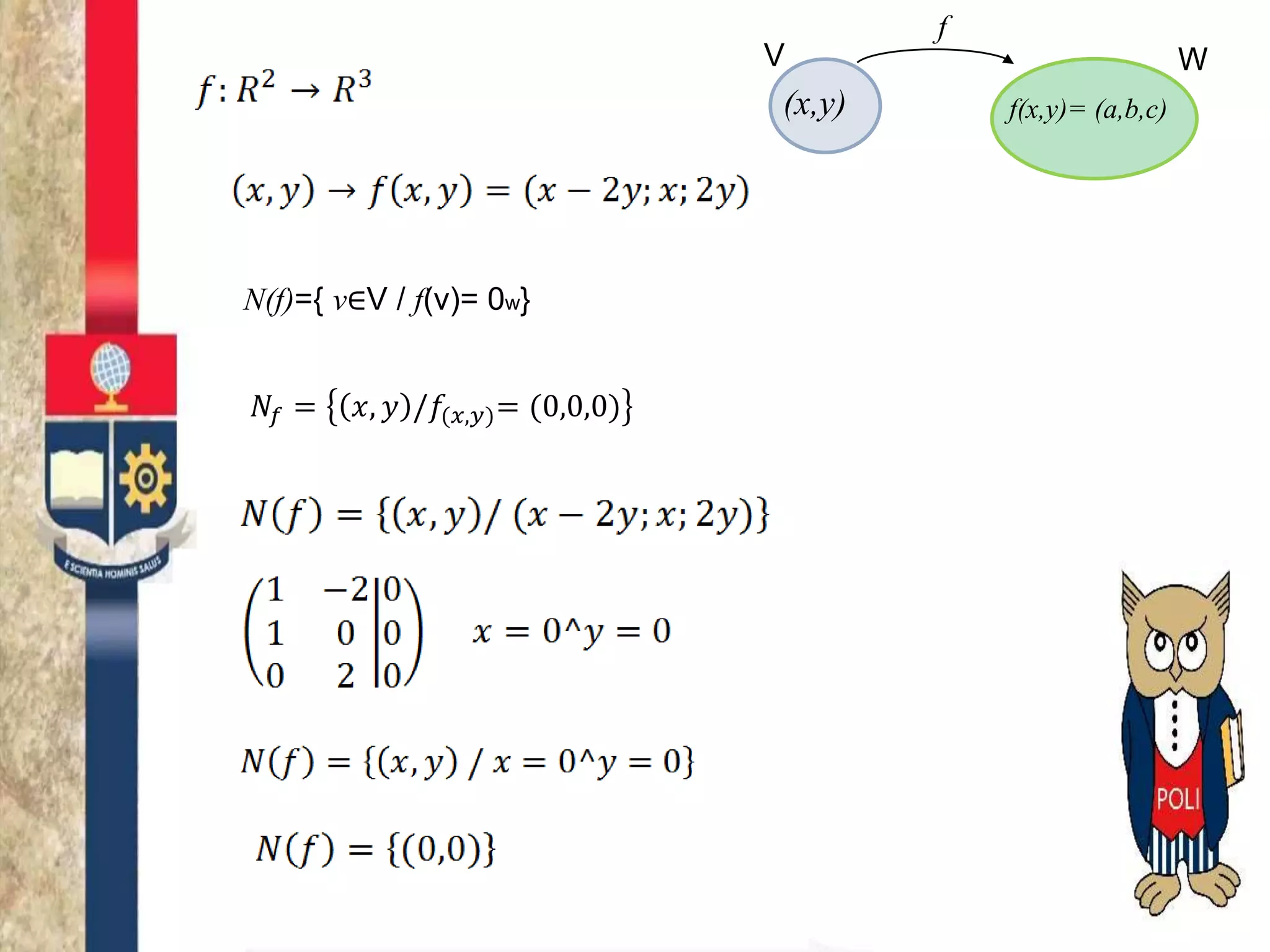
Este documento describe las propiedades y conceptos básicos de las transformaciones lineales entre espacios vectoriales. Explica que una transformación lineal f mapea vectores de un espacio vectorial V a vectores de un espacio vectorial W de tal manera que f(u+v)=f(u)+f(v) y f(αu)=αf(u). También define el núcleo como el subconjunto de vectores de V que se mapean al vector nulo en W, y la imagen como el subconjunto de vectores en W que son imágenes de vectores en V

1. ESCUELA POLITÉCNICA
NACIONAL
“El bienestar del hombre proviene de la Ciencia”
J O N AT H A N N A R A N J O
G R 4
G R U P O 5

2. V W
u f(u)= w
f
• Sean V y W dos espacios vectoriales definidos sobre el mismo campo.
Una función (aplicación) f de V en W ( f : V W ) que se asigna a cada
vector v ∈ V, un vector f(u)= w ∈W es una transformación lineal, si y solo
si, ∀∝∈ K, ∀u,v∈V, satisface lo siguiente:
f : V W
u f(u)= w
Estas dos son condiciones semejantes
Nota: se escribe f : V W para
indicar que f transforma el espacio
vectorial V en el espacio vectorial W.
TRANFORMACIONES LINEALES

3. Propiedades
Sea f : V W una transformación lineal, entonces se cumple que:
1. f(0v)= 0w
2. f(u-v)= f(u) - f(v)
3. Si 𝑆 es un subespacio vectorial de V, entonces 𝑓(S) es subespacio vectorial
de W.
4. Si T es subespacio vectorial de W, entonces 𝑓−1
(𝑇)
es subespacio vectorial
de V.
Ejemplo:
V W
(x,y) f(x,y)= (a,b,c)
f

4. Núcleo
Sea una transformación lineal, entonces el núcleo de f ,
notado por N(f) , es el subconjunto de V, que contiene todos los elementos
de v ∈ V, tales que sus imágenes son igual al vector nulo de W.
f : V W
V W
0w
x
x
ov
f
N(f)
X
X
N(f)={ v∈V / f(v)= 0w}

5. Imagen de la función
• Sea una transformación lineal, entonces la imagen de f ,
notado por 𝐼𝑚𝑔(f) , es el subconjunto de W, que contiene todos los
elementos de w ∈ W, que son imágenes de vectores 𝑣 Є 𝑉 debidas a la
transformación f.
• A la imagen de f también se la conoce como rango o recorrido de f.
f : V W
V W
x
x
x
f
Img(f)
W
Ov
x
Img(f)={ w∈W / ∃ v∈V , f(u)= w}

6. N(f)={ v∈V / f(v)= 0w}
V W
(x,y) f(x,y)= (a,b,c)
f
𝑁𝑓 = 𝑥, 𝑦 /𝑓(𝑥,𝑦)= (0,0,0)

7. Img(f)={ w∈W / ∃ v∈V v f(u)= w }