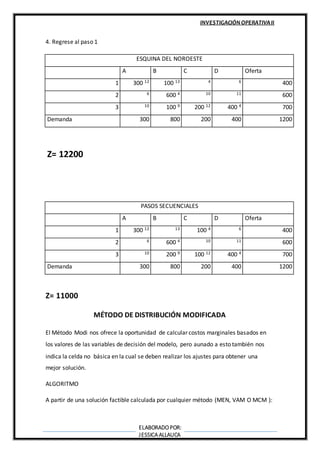
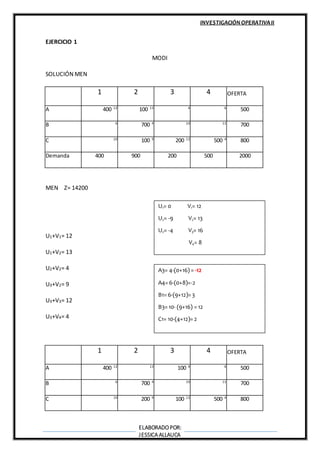
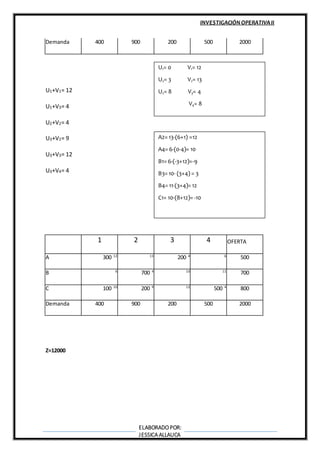
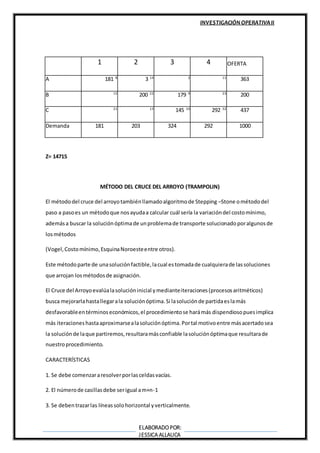
Este documento describe varios métodos para resolver problemas de asignación, incluyendo el método de pasos secuenciales, el método de distribución modificada, el método del cruce del arroyo y la programación cuadrática. Explica los algoritmos de cada método y cómo encontrar soluciones óptimas mediante iteraciones que mejoran la función objetivo.