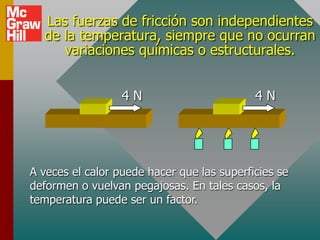
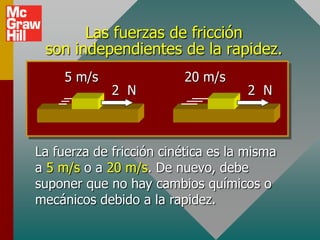
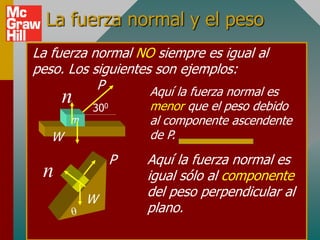
El documento trata sobre los conceptos de fricción estática y cinética. Explica que la fricción se opone al movimiento relativo entre dos superficies en contacto. Define los coeficientes de fricción estática y cinética, y establece que la fuerza de fricción es proporcional a la fuerza normal. También presenta ejemplos para ilustrar cómo aplicar los conceptos de fricción al análisis de problemas de equilibrio e iniciación del movimiento.

1. Fricción y equilibrio
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. Equilibrio: Hasta que inicia el movimiento,
todas las fuerzas sobre la podadora están
en balanceadas. La fricción sobre los
cojinetes de las ruedas y en el suelo se
oponen al movimiento lateral.

3. Objetivos: Después de completar
este módulo, deberá:
• Definir y calcular los coeficientes de fricción
cinética y estática, y dar la relación de
fricción a la fuerza normal.
• Aplicar los conceptos de fricción estática y
cinética a problemas que involucran
movimiento constante o movimiento
inminente.

4. Fuerzas de fricción
Cuando dos superficies están en contacto, las
fuerzas de fricción se oponen al movimiento
relativo o al movimiento inminente.
P
Las fuerzas de fricción son
paralelas a las superficies en
contacto y se oponen al
movimiento o movimiento
inminente.
Fricción estática: No Fricción cinética:
movimiento relativo. Movimiento relativo.

5. Fricción y fuerza normal
8N n 12 N n
4N
n2N 4N 6N
La fuerza que se requiere para superar la fricción estática
o cinética es proporcional a la fuerza normal, n.
fs = msn fk = mkn

6. Las fuerzas de fricción
son independientes del área.
4N 4N
Si la masa total que jala es constante, se requiere
la misma fuerza (4 N) para superar la fricción
incluso con el doble de área de contacto.
Para que esto sea cierto, es esencial que TODAS
las otras variables se controlen estrictamente.

7. Las fuerzas de fricción son independientes
de la temperatura, siempre que no ocurran
variaciones químicas o estructurales.
4N 4N
A veces el calor puede hacer que las superficies se
deformen o vuelvan pegajosas. En tales casos, la
temperatura puede ser un factor.

8. Las fuerzas de fricción
son independientes de la rapidez.
5 m/s 20 m/s
2 N 2 N
La fuerza de fricción cinética es la misma
a 5 m/s o a 20 m/s. De nuevo, debe
suponer que no hay cambios químicos o
mecánicos debido a la rapidez.

9. La fuerza de fricción estática
Cuando se intenta mover un objeto sobre
una superficie, la fricción estática aumenta
lentamente hasta un valor MÁXIMO.
n P
fs f s  ms n
W
En este módulo, cuando se use la siguiente
ecuación, se refiere sólo al valor máximo de la
fricción estática y se escribe simplemente:
fs = msn

10. Movimiento constante o inminente
Para el movimiento que es inminente y para el
movimiento con rapidez constante, la fuerza
resultante es cero y SF = 0. (Equilibrio)
fs P fk P
Reposo Rapidez constante
P – fs = 0 P – fk = 0
Aquí el peso y las fuerzas normales están
balanceadas y no afectan al movimiento.

11. Fricción y aceleración
Cuando P es mayor que el máximo fs la
fuerza resultante produce aceleración.
a Este caso se
fk P analizará en un
Rapidez constante
capítulo posterior.
fk = mkn
Note que la fuerza de fricción cinética permanece
constante incluso mientras aumenta la velocidad.

12. Ejemplo 1: Si mk = 0.3 y ms = 0.5, ¿qué jalón
horizontal P se requiere para apenas iniciar
el movimiento de un bloque de 250-N?
1. Dibuje bosquejo y diagrama
de cuerpo libre como se
muestra.
2. Mencione lo conocido y
n etiquete lo que se
P encontrará:
fs
+ mk = 0.3; ms = 0.5; W = 250 N
W
Encontrar: P = ¿? Para
apenas comenzar
3. Reconozca movimiento inminente: P – fs = 0

13. Ejemplo 1 (cont.): ms = 0.5, W = 250 N.
Encontrar P para superar fs (máx). Aplique
fricción estática.
n Para este caso: P – fs = 0
P 4. Para encontrar P necesita
fs
+ conocer fs , que es:
250 N fs = msn n=?
5. Para encontrar n: SFy = 0 n–W=0
W = 250 N n = 250 N
(continúa)

14. Ejemplo 1 (cont.): ms = 0.5, W = 250 N.
Encontrar P para superar fs (máx). Ahora se
conoce n = 250 N.
6. A continuación encuentre fs a
partir de: n
P
fs = msn = 0.5 (250 N) fs
7. Para este caso: P – fs = 0 +
250 N
P = fs = 0.5 (250 N)
ms = 0.5
P = 125 N
Esta fuerza (125 N) es necesaria para apenas iniciar el
movimiento. Considere a continuación P necesaria para
rapidez constante.

15. Ejemplo 1 (cont.): Si mk = 0.3 y ms = 0.5, ¿qué
jalón horizontal P se requiere para mover con
rapidez constante? (Superar fricción cinética)
SFy = may = 0
n-W=0 n=W
mk = 0.3
n
P Ahora: fk = mkn = mkW
fk
+ SFx = 0; P - fk = 0
mg
P = fk = mkW
P = (0.3)(250 N) P = 75.0 N

16. La fuerza normal y el peso
La fuerza normal NO siempre es igual al
peso. Los siguientes son ejemplos:
P Aquí la fuerza normal es
n 300 menor que el peso debido
m al componente ascendente
W de P.
P Aquí la fuerza normal es
n igual sólo al componente
del peso perpendicular al
W
plano.

17. Repaso de diagramas de cuerpo libre:
Para problemas de fricción:
• Lea el problema; dibuje y etiquete bosquejo.
• Construya diagrama de fuerzas para cada objeto,
vectores en el origen de los ejes x, y. Elija el eje x
el y a lo largo del movimiento o movimiento
inminente.
• Puntee rectángulos y etiquete los componentes x y
y opuesto y adyacente a los ángulos.
• Etiquete todos los componentes; elija dirección
positiva.

18. Para fricción en equilibrio:
• Lea, dibuje y etiquete el problema.
• Dibuje diagrama de cuerpo libre para cada cuerpo.
• Elija el eje x o y a lo largo del movimiento o
movimiento inminente y elija la dirección de
movimiento como positiva.
• Identifique la fuerza normal y escriba una de las
siguiente:
fs = msn o fk = mkn
• Para equilibrio, escriba para cada eje:
SFx = 0 SFy = 0
• Resuelva para cantidades desconocidas.

19. Ejemplo 2. Una fuerza de 60 N arrastra un bloque
de 300-N mediante una cuerda a un ángulo de 400
sobre la superficie horizontal. Si uk = 0.2, ¿qué
fuerza P producirá rapidez constante?
1. Dibuje y etiquete un
W = 300 N P=?
bosquejo del problema.
n 400 2. Dibuje diagrama de cuerpo
fk libre.
m
P sen 400 Py
P
W
n Py
400
Se sustituye la fuerza P
Px
por sus componentes fk P cos 400
Px y Py.
W +

20. Ejemplo 2 (cont.). P = ¿?; W = 300 N; uk = 0.2.
3. Encuentre componentes P sin 400
P
de P: n
Px = P cos 400 = 0.766P 400
Py = P sen 400 = 0.643P fk P cos 400
mg +
Px = 0.766P; Py = 0.643P
Nota: Las fuerzas verticales están balanceadas y, para
rapidez constante, las fuerzas horizontales están
balanceadas.
F x 0 F y 0

21. Ejemplo 2 (cont.). P = ¿?; W = 300 N; uk = 0.2.
Px = 0.766P 0.643P
Py = 0.643P P
n
4. Aplique condiciones 400
de equilibrio al eje fk 0.766P
vertical.
300 N +
SFy = 0
n + 0.643P – 300 N= 0 [Py y n son arriba (+)]
n = 300 N – 0.643P; Resuelva para n en
términos de P
n = 300 N – 0.643P

22. Ejemplo 2 (cont.). P = ¿?; W = 300 N; uk = 0.2.
0.643P
n = 300 N – 0.643P n
P
5. Aplique SFx = 0 a 400
movimiento horizontal fk 0.766P
constante.
300 N +
SFx = 0.766P – fk = 0
fk = mk n = (0.2)(300 N - 0.643P)
fk = (0.2)(300 N - 0.643P) = 60 N – 0.129P
0.766P – fk = 0; 0.766P – (60 N – 0.129P) = 0

23. Ejemplo 2 (cont.). P = ¿?; W = 300 N; uk = 0.2.
0.643P
P 0.766P – (60 N – 0.129P
n 6. Resuelva para incógnita P.
400 )=0
fk 0.766P
300 0.766P – 60 N + 0.129P =0
N +
0.766P + 0.129P = 60 N Si P = 67 N, el
bloque se
0.766P + 0.129P = 60 N arrastrará con
rapidez constante.
0.895P = 60 N
P = 67.0 N P = 67.0 N

24. Ejemplo 3: ¿Qué empuje P sobre el plano se
necesita para mover un bloque de 230 N arriba
del plano con rapidez constante si mk = 0.3?
Paso 1: Dibuje cuerpo P
libre, incluidos fuerzas,
W =230 N
ángulos y componentes.
y n P
x
Paso 2: SFy = 0
fk
W sen 600
W cos 600
n – W cos 600 = 0
600
n = (230 N) cos 600
230 N
n = 115 N

25. Ejemplo 3 (cont.): Encuentre P
para dar movimiento sobre el plano
(W = 230 N).
y n P
x
n = 115 N W = 230 N
fk W cos 600
Paso 3. Aplique SFx= 0
W sen 600 600 P - fk - W sen 600 = 0
fk = mkn = 0.2(115 N)
W
fk = 23 N, P = ¿?
P - 23 N - (230 N) sen 600 = 0
P - 23 N - 199 N= 0 P = 222 N

26. Resumen: Puntos importantes a considerar
cuando resuelva problemas de fricción.
• La fuerza máxima de fricción estática es la
fuerza requerida para apenas iniciar el
movimiento.
n P
fs f s  ms n
W
En ese instante existe equilibrio:
SFx  0; SFy  0

27. Resumen: Puntos importantes (cont.)
• La fuerza de fricción cinética es aquella requerida
para mantener movimiento constante.
n P
fk
f k  mk n
W
• Existe equilibrio si la rapidez es
constante, pero fk no se hace más
grande conforme la rapidez aumenta.
SFx  0; SFy  0

28. Resumen: Puntos importantes (cont.)
• Elija eje x o y a lo largo de la dirección de
movimiento o movimiento inminente.
La SF será zero a lo
largo del eje x y del
mk = 0.3
n eje y.
P
fk
+
En esta figura se tiene:
W
SFx  0; SFy  0

29. Resumen: Puntos importantes (cont.)
• Recuerde: la fuerza normal n no siempre
es igual al peso de un objeto.
P
n 300
Es necesario dibujar el
m diagrama de cuerpo
W libre y sumar las
fuerzas para encontrar
P
n el valor correcto de n.
W SFx  0; SFy  0

30. Resumen
Fricción estática: No Fricción cinética:
movimiento relativo. Movimiento relativo.
fs ≤ msn fk = mkn
El procedimiento para la solución de
problemas de equilibrio es el mismo para
cada caso:
SFx  0 SFy  0

31. Conclusión:
Fricción y equilibrio