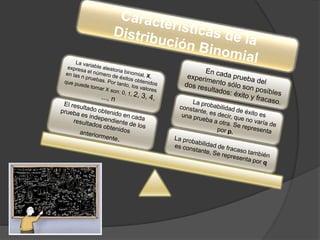
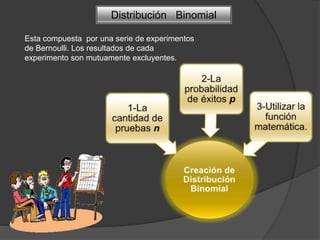
Este documento presenta información sobre la distribución binomial. Explica que fue estudiada por Jakob Bernoulli y también menciona a Gauss y su estudio de la distribución normal. Luego presenta ejemplos numéricos para calcular probabilidades usando la fórmula binomial en diferentes escenarios como el servicio al cliente y la validación de solicitudes de empleo. Finalmente señala que la distribución binomial se aplica en situaciones cotidianas aunque de manera más simple que el tratamiento matemático formal.

1. Alumno: Florangel Amaro
C.I: 18.103.820
Sección SAIA Grupo A
Nombre del Docente José Ernesto Linárez
Nombre de la asignatura: Tecnicas
Estadísticas Avanzadas
Universidad “Fermín Toro”
Faculta de Ciencias Económicas y Sociales
Escuela de Administración y Relaciones Industriales.
Distribución Binomial

2. Distribución Binomial
Fue estudiada por Jakob Bernoulli (Suiza, 1654-1705), quien escribió
el primer tratado importante sobre probabilidad, “Ars conjectandi” (El
arte de pronosticar).
También se desataca, la distribución normal es un ejemplo de las
distribuciones continuas, y aparece en multitud de fenómenos
sociales. Fue estudiada, entre otros, por J.K.F. Gauss
(Alemania,1777-1855), uno de los más famosos matemáticos de la
historia. La gráfica de la distribución normal en forma de campana se
denomina Campana de Gauss.
Jakob Bernoulli Johann Karl Friedrich Gauss

4. Distribución Binomial
Esta compuesta por una serie de experimentos
de Bernoulli. Los resultados de cada
experimento son mutuamente excluyentes.

5. Ejercicio Nº 1
En una oficina de servicio al cliente se atienden 100 personas diarias. Por lo general 10 personas se
van sin recibir bien el servicio. Determine la probabilidad de que en una encuesta a 15 clientes :
a) 3 no hayan recibido un buen servicio
b) Ninguno haya recibido un buen servicio
c) A lo más 4 personas recibieron un buen servicio
d) Entre 2 y cinco personas
Formula P(n,k,p)=(n/k)(pk1-p)n-k
a) n=15
k=3
p=10/100=0.1
p=(n,k,p)=(15/3)(0.1)3(1-0.1)15-3
=(15/6)(0.1)(3(0.9)15
=455(0.001)(0.2824)
=0.1285x100%= 12,85%
La probabilidad de que 3 recibieran un buen servicio es de 12,85%

6. b) n=15
k=0
p=10/100=0.1
p=(n,k,p)=(15/0)(0.1)3(1-0.1)15-0
=1. (1)(09)15
=0.2059x100%
=20.59%
La probabilidad de que ninguno recibiera un buen servicio es de 20.59%
c) n=15
k=4
p= 10/100=0.1
P=(x≤4) P=(n,n,p)=(15/4).(0.1)4(1-0.1)15-4
= 1362(0.0001).(0.9)11
= 1362(0,0001) (0.3138)
= 0,428X100% = 4,28
La probabilidad de que más de 4 personas recibieran un buen servicio es de 4,28%

7. d) n=15
k=2
p=10/100=0.1
P(n,k,p)=15/2(0.1)2(1-0.1) 15-2
=105(0.01)(0.2541)
=0266803X100% = 26.68%
n=15
k= 5
P=10/100=01
P(n,kp)=(15/1)(0.1)1(1-0.1)15-1
= 15(0.1)(0,2287)
= 0.34305X100% =34.30%
k0+k1+k2+k3+k4
26,59%+34,30%+26,68%+12,85%+4,28%
n=15
k=5
p=10/100=0.1
=(15/5)(0.1)5(1.0.1)10-5
=3003(0,00001)(0.3486)
=0.01046X100% = 1.04%
La probabilidad de entre 2 y 5 personas es de 44,85%

8. Ejercicio Nº 2
Muchos jefes se dan cuenta de que algunas de las personas que contrataron no son lo que pretenden ser.
Detectar personas que solicitan un trabajo y que falsifican la información en su solicitud ha generado un
nuevo negocio. Una revista nacional notificó sobre este problema mencionando que una agencia, en un
periodo de dos meses, encontró que el 35% de los antecedentes examinados habían sido alterados.
Suponga que usted ha contratado la semana pasada 5 nuevos empleados y que la probabilidad de que un
empleado haya falsificado la información en su solicitud es 0.35.
a)¿Cuál es la probabilidad de que al menos una de las cinco solicitudes haya sido falsificada?
b)¿Ninguna de las solicitudes haya sido falsificada?
c)¿Las cinco solicitudes hayan sido falsificadas?
a) n=5
k=01
P=0.35 P
(n.k.p)=(n/k)pk(1-p)n-k
P=(n,k,p)=(5/1)(0.035)1(1-0.35)5-1
=(5/1)(0.35)1(0.33)1(0.1785)
=5(0.5)(0.1785)
=0.445X100% =44.5%
La probabilidad de que al menos una de las 5 solicitudes sea falsificada es de 44.5%

9. b) n=5
k=0
P=0.35
P=(n,k,p)=(n/k)p(1-p)n-k
P=(n,k,p)=(5/0)(0.35)(1-0.35)5-0
P= (5/0)(0.35)°(0.1160)
=0.1160X100% =11,60%
La probabilidad que ninguna de las solicitudes sean falsificadas es de un 11,60%
c) n=5
k=5
p=0.35
(n/k)pk(1-p)n-k
(5/5)(0.35)5(1-0.35)5-5
1(0,0052)(0.65)
=0.0033X100% =0.33%
La probabilidad de que las 5 solicitudes sean falsificadas es de 0.33%

10. Se puede decir que esta distribución
binomial la utilizamos en algunas
situaciones de nuestras vida cotidiana,
aunque de una manera mas sencilla y
practica, aunque no cumpliendo con el
ejercicio como deber ser con los pasos
con y las formulas de las cuales se deben
proceder para el buen uso de función de
esta teoría.