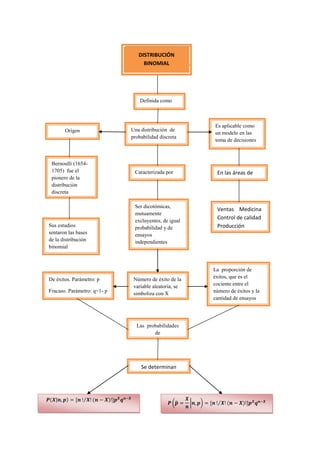
Este documento describe la distribución binomial. Explica que la distribución binomial modela el número de éxitos en una serie de ensayos independientes idénticos con dos posibles resultados. Resuelve ejemplos numéricos calculando probabilidades usando la fórmula binomial.

1. UNIVERSIDAD “FERMIN TORO”
Facultad de Ciencias Económicas y Sociales
Escuela de Administración y Relaciones Industriales
Aroldo Castro
C.I. 13.040.704

2. Origen
Una distribución de probabilidad discreta
Sus estudios sentaron las bases de la distribución binomial
Es aplicable como un modelo en las toma de decisiones
Caracterizada por
Definida como
Bernoulli (1654- 1705) fue el pionero de la distribución discreta
Número de éxito de la variable aleatoria, se simboliza con X
Ser dicotómicas, mutuamente excluyentes, de igual probabilidad y de ensayos independientes
Las probabilidades de
Se determinan
La proporción de éxitos, que es el cociente entre el número de éxitos y la cantidad de ensayos
De éxitos. Parámetro: p
Fracaso. Parámetro: q=1- p
( | ) ( ) ⁄
( ̂ | ) ( ) ⁄
En las áreas de
Ventas Medicina Control de calidad Producción
DISTRIBUCIÓN BINOMIAL

3. PROBLEMAS RESUELTOS
1. En una oficina de servicio al cliente se atienden 100 personas diarias. Por lo general 10 personas se van sin recibir bien el servicio. Determine la probabilidad de que en una encuesta a 15 clientes
a) 3 no hayan recibido un buen servicio
b) Ninguno haya recibido un buen servicio
c) A lo más 4 personas recibieron un buen servicio
d) Entre 2 y cinco personas
SOLUCIÓN
Datos
Sea la variable X: Recibió un buen servicio.
q =10% = 0.10.
p=1- q p = 1 -.0.10 = 0.90
n = 15
Fórmula: ( | ) ( )
a) Si 3 no recibieron buen servicio entonces de las 15 personas encuestadas 12 estuvieron bien atendidos. Esto es, X = 12. ( | ) ( ⁄)
3170* .
b) Si ninguno fue bien atendido entonces
( | ) ( ⁄)
c) A los más 4 reciben buen servicio implica que X= 0, 1, 2, 3 y 4
( | ) ( ( ) ⁄)
( | ) ( ( ) ⁄)
( | ) ( ( ) ⁄)

4. ( | ) ( ( ) ⁄)
( | ) ( ( ) ⁄) ( | ) ( | )
d) Si dan un buen servicio entre 2 y 5 personas entonces X = 2, 3, 4 y 5
Como en el literal c) se encontró que
( | )
( | ) ( | )
solo falta resolver para X= 5
(X 5|15; 0.10) ( ⁄)
( | )
( | ) 0,4487
2. Muchos jefes se dan cuenta de que algunas de las personas que contrataron no son lo que pretenden ser. Detectar personas que solicitan un trabajo y que falsifican la información en su solicitud ha generado un nuevo negocio. Una revista nacional notificó sobre este problema mencionando que una agencia, en un periodo de dos meses, encontró que el 35% de los antecedentes examinados habían sido alterados. Suponga que usted ha contratado la semana pasada 5 nuevos empleados y que la probabilidad de que un empleado haya falsificado la información en su solicitud es 0.35.
a) ¿Cuál es la probabilidad de que al menos una de las cinco solicitudes haya sido falsificada?
b) ¿Ninguna de las solicitudes haya sido falsificada?
c) ¿Las cinco solicitudes hayan sido falsificadas?

5. SOLUCIÓN
Datos
n = 5
Variable X: Información falsificada
P = 0,35 y q = 1 – 0,35 = 0,65
a) (X 1|5; 0.35) ( ( ⁄))
b) (X 0|5; 0.35) ( ( ⁄))
c) (X 5|5; 0.35) ( ( ⁄))